• PID算法
  • 串级PID控制
  • 参考
• Probabilistic Robotics
  • 贝叶斯过滤器
  • 递归最小二乘法
  • 零点 & 极点
• Kalman filters

PID算法

PID算法是自动控制领域最基础应用也最广泛的算法。它是三个单词proportional（P，比例）、integral（I，积分）和differential（D，微分）的缩写。

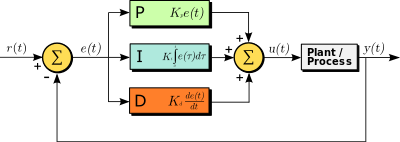
PID算法的流程如下图所示：

图1

以下我们以水箱水龙头为例，解释一下PID算法的各个要素。

场景1：假设我们面对的系统是一个简单的水箱的液位，要从空箱开始注水直到达到某个高度，而你能控制的变量是注水龙头的开关大小。

图1中的\(r(t)\)表示期待的设定值，在这个场景中，就是水箱的液位。\(y(t)\)表示当前的液位。\(e(t)=r(t)-y(t)\)表示误差值。

针对这个场景，我们可以设计如下算法：

水箱液位离预定高度远的时候开关开大点，离的近的时候开关就开小点，随着液位逐步接近预定高度逐渐关掉水龙头。用数学表示就是：

\[u(t) = K_\text{p} e(t)\tag{1}\]

上式中的\(u(t)\)表示需要控制的量，在这里就是水龙头的开合度。\(K_\text{p}\)被称为比例系数。

场景2：假设这个水箱不仅仅是装水的容器了，还需要持续稳定的给用户供水。

以下用c表示给用户供水的量(\(c\ge 0\))。显然如果使用公式1，则系统稳定时，\(u(t)-c=0\)，即\(K_\text{p} e(t)=c\)。

由于c和\(K_\text{p}\)都不为0，因此\(e(t)\)也不为0，这就导致始终无法加注到指定水位。这种稳态误差被称为静差。

为了平衡c，我们修改算法为：

\[u(t) = K_\text{p} e(t) + K_\text{i} \int_0^t e(\tau) \,d\tau\tag{2}\]

\(K_\text{i}\)被称为积分系数。积分环节的意义就相当于你增加了一个水龙头，这个水龙头的开关规则是水位比预定高度低就一直往大了拧，比预定高度高就往小了拧。如果漏水速度不变，那么总有一天这个水龙头出水的速度恰好跟漏水的速度相等了，系统就和第一小节的那个一样了。那时，静差就没有了。这就是所谓的积分环节可以消除系统静差。

场景3：假设用户的用水量是变化的，即\(c(t)\)。

这时，如果仍采用公式2，则由于\(c(t)\)的变化，导致\(e(t)\)不恒为0。为了减小\(c(t)\)的变化，对\(e(t)\)的影响，我们继续修改算法：

\[u(t) = K_\text{p} e(t) + K_\text{i} \int_0^t e(\tau) \,d\tau + K_\text{d} \frac{de(t)}{dt}\tag{3}\]

\(K_\text{d}\)被称为微分系数。由于\(c(t)\)的变化不可能事先得知，因此，微分环节只能减小\(c(t)\)的变化所造成的影响，而不能消除。

公式3在Laplace域可写做：

\[L(s) = K_\text{p} + K_\text{i}/s + K_\text{d} s\tag{4}\]

从公式4可以看出，PID controller的数学原理和锁相环（Phase-locked loop）非常类似，它们实际上都是Feedback Control系统。

---

反馈控制最重要的就是两点：

一是反馈；

二是测量的大方向。

只要有反馈的结构在，只要测量的反馈值正负号不搞错，那其他的都只是细枝末节的问题了。

https://www.zhihu.com/question/47755808

常用控制算法（包括PID和卡尔曼滤波等）各有什么天然的局限乃至缺陷？

串级PID控制

实际使用中，为了改善PID控制的效果，一般还会用到串级PID控制。

参考：

https://blog.csdn.net/qq_25005909/article/details/77941243

串级PID控制四轴飞行状态-分析

https://blog.csdn.net/nemol1990/article/details/45131603

四轴PID讲解

https://www.zhihu.com/question/293450508

飞控算法中双环串级PID如何理解?

参考

https://en.wikipedia.org/wiki/PID_controller

《Feedback Control of Dynamic Systems》，Gene F. Franklin，J David Powell，Abbas Emami-Naeini著。

Gene F. Franklin，1927~2012，美国控制论学家。哥伦比亚大学博士，斯坦福大学教授。

J David Powell，美国航空航天学家。斯坦福大学博士和教授。

Abbas Emami-Naeini，斯坦福大学博士和讲师，SC Solutions公司总监。

https://www.zhihu.com/answer/23942834

如何通俗地解释PID参数整定？

https://zhuanlan.zhihu.com/p/35473808

PID控制器的贝叶斯理解

https://zhuanlan.zhihu.com/p/139244173

广告出价–如何使用PID控制广告投放成本

https://zhuanlan.zhihu.com/p/39573490

PID控制算法原理

https://mp.weixin.qq.com/s/4iX1hB_f8zQYrG0EQ2u3wA

PID算法在广告成本控制领域的应用

https://mp.weixin.qq.com/s/__xvATWhggYXLy92dz9L5Q

广告成本控制-PID算法

https://mp.weixin.qq.com/s/fswZL2qhgErccYB1GuXZ8g

PID微分器与滤波器的爱恨情仇

https://mp.weixin.qq.com/s/vsyEM7z7-tKrXwRPjE5-EA

浅谈PID控制对无人车/船的自动驾驶影响及水信无人船PID调试结果展示

Probabilistic Robotics

这篇心得主要根据Sebastian Thrun的Probabilistic Robotics课程的ppt来写。

Sebastian Thrun，德国波恩大学博士（1995年）。先后执教于CMU和Stanford。

网址：

http://robots.stanford.edu/probabilistic-robotics/ppt/

贝叶斯过滤器

假定我们需要根据测量值z来判断门的开关。显然，这里的\(P(open\mid z)\)是诊断式（diagnostic）问题，而\(P(z\mid open)\)是因果式（causal）问题。通常来说，后者比较容易获取，而前者可以基于后者使用贝叶斯公式计算得到。

一般将\(P(z\mid x)\)称为Sensor model。

针对多相关测量值问题，这里有一个和朴素贝叶斯假设相仿的Markov assumption——假设\(z_n\)独立于\(z_1,\dots,z_{n-1}\)（即“现在”不依赖于“过去”），则：

\[\begin{array}\\ P(x\mid z_1,\dots,z_n)=\frac{P(z_n\mid x)P(x\mid z_1,\dots,z_{n-1})}{P(z_n\mid z_1,\dots,z_{n-1})}(\text{Bayes})\\ =\eta P(z_n\mid x)P(x\mid z_1,\dots,z_{n-1})=\eta_{1,\dots,n}\prod_{i=1}^nP(z_i\mid x)P(x)(\text{Markov}) \end{array}\]

以下的推导过程注释中，如无特别说明。均以Bayes指代Bayes’ theorem，以Markov指代Markov assumption。

上式中的\(\eta\)表示概率的归一化系数。

除了测量值z之外，一般的控制系统中还有动作（Action）的概念。比如打开门就是一个Action。Action会导致系统的状态发生改变（也可不变）。如下图所示：

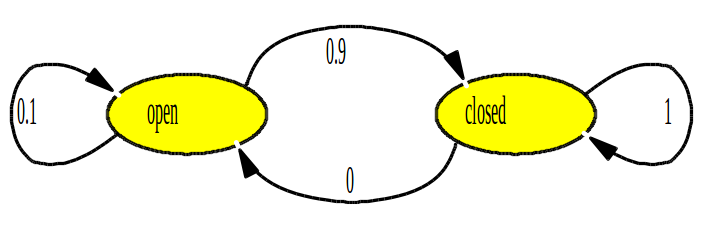
通常，将\(P(x\mid u,x')\)称作Action Model。其中，u表示Action，而x’表示系统的上一个状态。

一般的，新的测量值会减少系统的不确定度，而新的Action会增加系统的不确定度。

综上，一个贝叶斯过滤器（Bayes Filters）的框架包括：

输入：

1.观测值z和Action u的序列：\(d_t=\{u_1,z_1,\dots,u_t,z_t\}\)

2.Sensor model：\(P(z\mid x)\)

3.Action model：\(P(x\mid u,x')\)

4.系统状态的先验概率：\(P(x)\)

输出：

1.估计动态系统的状态X。

2.状态的后验概率，也叫Belief：

\[\begin{align} \mathbf{Bel(x_t)}&=P(x_t\mid u_1,z_1,\dots,u_t,z_t) \\&=\eta P(z_t\mid x_t,u_1,z_1,\dots,u_t)P(x_t\mid u_1,z_1,\dots,u_t)(\text{Bayes}) \\&=\eta P(z_t\mid x_t)P(x_t\mid u_1,z_1,\dots,u_t)(\text{Markov}) \\&=\eta P(z_t\mid x_t)\int P(x_t\mid u_1,z_1,\dots,u_t,x_{t-1})P(x_{t-1}\mid u_1,z_1,\dots,u_t)\mathrm{d}x_{t-1}(\text{Total prob.}) \\&=\eta P(z_t\mid x_t)\int P(x_t\mid u_t,x_{t-1})P(x_{t-1}\mid u_1,z_1,\dots,u_t)\mathrm{d}x_{t-1}(\text{Markov}) \\&=\eta P(z_t\mid x_t)\int P(x_t\mid u_t,x_{t-1})P(x_{t-1}\mid u_1,z_1,\dots,z_{t-1})\mathrm{d}x_{t-1}(\text{Markov}) \\&=\eta P(z_t\mid x_t)\int P(x_t\mid u_t,x_{t-1})\mathbf{Bel(x_{t-1})}\mathrm{d}x_{t-1} \end{align}\]

上式也可以写作：

预测：

\[\overline{\mathbf{Bel(x_t)}}=\int P(x_t\mid u_t,x_{t-1})\mathbf{Bel(x_{t-1})}\mathrm{d}x_{t-1}\]

修正：

\[\mathbf{Bel(x_t)}=\eta P(z_t\mid x_t)\overline{\mathbf{Bel(x_t)}}\]

熟悉卡尔曼滤波的同学大概已经看出来了。没错！贝叶斯过滤器是一大类算法的统称。这些算法包括Kalman filters、Particle filters、Hidden Markov models、Dynamic Bayesian networks、Partially Observable Markov Decision Processes (POMDPs)等。

递归最小二乘法

Recursive Least Squares

http://www.doc88.com/p-6836102414531.html

RLS自适应算法基本原理

https://blog.csdn.net/HJ199404182515/article/details/52504150

浅谈自适应滤波器

零点 & 极点

John Doyle举过一个很直观的例子: 把一根杆立在手上，保持不倒。

杆越长就越容易。杆的长度会影响极点的位置，杆越短的话极点越不稳定。

一般人做这个实验的时候是眼睛看杆的顶端。如果眼睛只盯着杆的中心，这个任务也会变得非常难。原因是因为零点的位置，导致杆的状态变得不可观。

控制系统中的零极点有什么物理意义么？

Kalman filters

Rudolf (Rudi) Emil Kálmán，1930～2016，匈牙利出生的美国科学家。哥伦比亚大学博士（1957），先后执教于斯坦福大学和佛罗里达大学。现代控制理论的里程碑人物，美国科学院院士。
卡尔曼滤波从纯数学的角度讲，并没有多大意义。因此，主流数学家们在很长一段时间内，并不承认Kálmán是数学家。只是由于卡尔曼滤波在工程界的巨大影响力，才不得不于2012年，授予其美国数学协会院士。

名称	使用场景
Kalman filters	Linear Gaussian
Extended Kalman filter	Nonlinear Gaussian
Iterated EKF	Nonlinear Gaussian
Unscented Kalman filters	Nonlinear Gaussian
Particle filter	Nonlinear Non-Gaussian

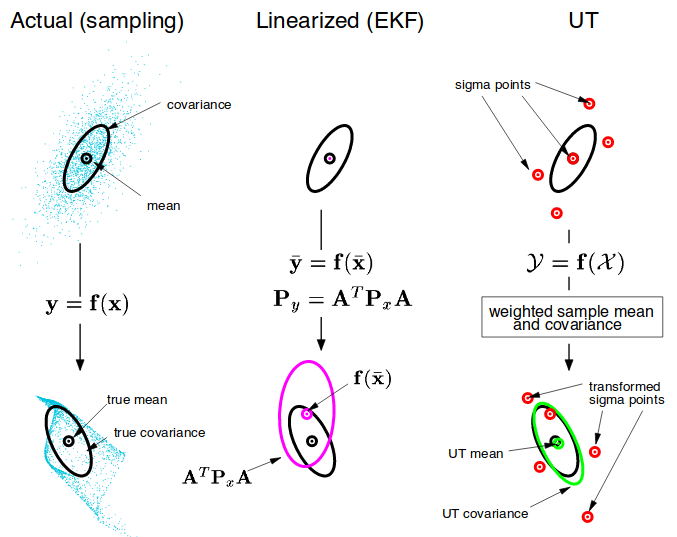
unscented transformation

参考：

http://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf

Gregory Francis Welch写的卡尔曼滤波科普文。

Gregory Francis Welch，北卡罗莱娜大学博士（1997）。中佛罗里达大学教授。

http://www.cs.unc.edu/~welch/kalman/media/misc/kalman_intro_chinese.zip

上文的中文版。

https://zhuanlan.zhihu.com/p/21294526

知乎诸位大神的科普文。

http://www.docin.com/p-976961701.html

动态相对定位中自适应滤波方法的研究

《自适应动态导航定位》，杨元喜著。

杨元喜，1956年生，大地测量学家。中国科学院院士。

https://zhuanlan.zhihu.com/c_1131936304564453376

专栏：现代控制理论

https://zhuanlan.zhihu.com/ClassicControl

专栏：经典控制理论

https://blog.csdn.net/tiandijun/article/details/72469471

通俗理解卡尔曼滤波及其算法实现