机器学习（三十四）——机器学习语录, Linear Discriminant Analysis
2018-01-31机器学习语录
这里收录一些网上的只言片语式的心得，以区别于一般的教程。
首先要考虑你的数据维度是线性相关的还是非线性相关的，数据是稀疏的还是稠密的，正例反例比例是多少，数据量是否充足。数据是否具有可分类性。是否需要降维。是否有噪音，是否有异常点等，然后去选择分类策略。通常包括数据采集，预处理，分类训练，预测，后处理等过程。
角度值的特征化
角度值是数据分析中常见的值，然而它不是线性的，比如0度和359度之间只相差1度，然而数值上却差了359度，因此无法将角度值直接代入线性回归等模型。因为后者的loss函数是用线性的欧氏距离定义的，角度显然不满足要求。
既然角度在一维上不是线性的，那么二维呢？没错，可以采用复数坐标(x,y)来表示角度，这样角度就是线性的了。
相关关系不等同于因果关系
我们可以通过一句调侃的话来解释：“地球变暖、地震、龙卷风，以及其他自然灾害，都和18世纪以来全球海盗数量的减少有直接关系”。这两个变量的变化有相关性，但是并不能说存在因果关系，因为往往存在第三类（甚至第4、5类）未被观察到的变量在起作用。相关关系应该看作是潜在的因果关系的一定程度的体现，但需要进一步研究。
Linear Discriminant Analysis
在《机器学习（二十六）》中，我们已经讨论了一个LDA，这里我们来看看另一个LDA。
Linear Discriminant Analysis是Ronald Fisher于1936年提出的方法，因此又叫做Fisher’s linear discriminant。正如之前在《知名数据集》中提到的，Iris flower Data Set也是出自该论文。
之前我们讨论的PCA、ICA也好，对样本数据来言，可以是没有类别标签y的。回想我们做回归时，如果特征太多，那么会产生不相关特征引入、过度拟合等问题。我们可以使用PCA来降维，但PCA没有将类别标签考虑进去，属于无监督的。
比如回到上次提出的文档中含有“learn”和“study”的问题，使用PCA后，也许可以将这两个特征合并为一个，降了维度。但假设我们的类别标签y是判断这篇文章的topic是不是有关学习方面的。那么这两个特征对y几乎没什么影响，完全可以去除。
再举一个例子，假设我们对一张100*100像素的图片做人脸识别，每个像素是一个特征，那么会有10000个特征，而对应的类别标签y仅仅是0/1值，1代表是人脸。这么多特征不仅训练复杂，而且不必要特征对结果会带来不可预知的影响，但我们想得到降维后的一些最佳特征（与y关系最密切的），怎么办呢？
给定特征为d维的N个样例\(x^{(i)}\{x_1^{(i)},x_2^{(i)},\dots,x_d^{(i)}\}\)，其中有\(N_1\)个样例属于类别\(w_1\)，另外\(N_2\)个样例属于类别\(w_2\)。
现在我们觉得原始特征数太多，想将d维特征降到只有一维，而又要保证类别能够“清晰”地反映在低维数据上，也就是这一维就能决定每个样例的类别。
我们将这个最佳的向量称为w（d维），那么样例x（d维）到w上的投影可以用下式来计算：
\[y=w^Tx\]这里得到的y值不是0/1值，而是x投影到直线上的点到原点的距离。
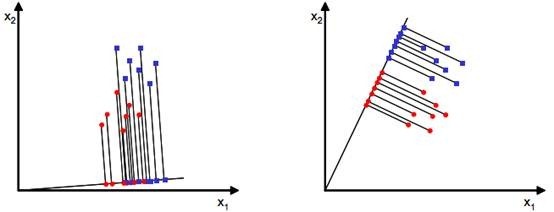
我们首先看看x是二维的情况，从直观上来看，右图比较好，可以很好地将不同类别的样本点分离。这实际上就是LDA的思想：最大化类间方差与最小化类内方差，即减少分类内部之间的差异，而扩大不同分类之间的差异。
接下来我们从定量的角度来找到这个最佳的w。
首先我们寻找每类样例的均值（中心点），这里i只有两个：
\[\mu_i=\frac{1}{N_i}\sum_{x\in \omega_i}x\]由于x到w投影后的样本点均值为：
\[\tilde{\mu_i}=\frac{1}{N_i}\sum_{y\in \omega_i}y=\frac{1}{N_i}\sum_{y\in \omega_i}w^Tx=w^T\mu_i\]由此可知，投影后的的均值也就是样本中心点的投影。
什么是最佳的直线（w）呢？我们首先发现，能够使投影后的两类样本中心点尽量分离的直线是好的直线，定量表示就是：
\[J(w)=\mid \tilde{\mu_1}-\tilde{\mu_2} \mid=\mid w^T(\mu_1-\mu_2) \mid\]J(w)越大越好。
但是只考虑J(w)行不行呢？不行，看下图：
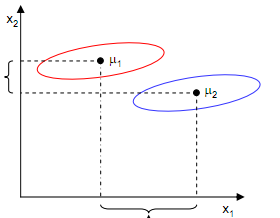
样本点均匀分布在椭圆里，投影到横轴\(x_1\)上时能够获得更大的中心点间距J(w)，但是由于有重叠，\(x_1\)不能分离样本点。投影到纵轴\(x_2\)上，虽然J(w)较小，但是能够分离样本点。因此我们还需要考虑样本点之间的方差，方差越大，样本点越难以分离。
我们使用另外一个度量值，称作散列值（scatter），对投影后的类求散列值，如下：
\[\tilde{s_i}^2=\sum_{y\in \omega_i}(y-\tilde{\mu_i})^2\]从公式中可以看出，只是少除以样本数量的方差值，散列值的几何意义是样本点的密集程度，值越大，越分散，反之，越集中。
而我们想要的投影后的样本点的样子是：不同类别的样本点越分开越好，同类的越聚集越好，也就是均值差越大越好，散列值越小越好。正好，我们可以使用J(w)和S来度量，最终的度量公式是：
\[J(w)=\frac{\mid \tilde{\mu_1}-\tilde{\mu_2} \mid}{\tilde{s_1}^2+\tilde{s_2}^2}\]接下来的事就比较明显了，我们只需寻找使J(w)最大的w即可。
先把散列值公式展开：
\[\tilde{s_i}^2=\sum_{y\in \omega_i}(y-\tilde{\mu_i})^2=\sum_{x\in \omega_i}(w^Tx-w^T\mu_i)^2=\sum_{x\in \omega_i}w^T(x-\mu_i)(x-\mu_i)^Tw\]我们定义上式中间部分：
\[S_i=\sum_{x\in \omega_i}(x-\mu_i)(x-\mu_i)^T\]这也被称为散列矩阵（scatter matrices）。
我们继续定义：
\[S_W=S_1+S_2\]\(S_W\)称为Within-class scatter matrix。
\[S_B=(\mu_1-\mu_2)(\mu_1-\mu_2)^T\]\(S_B\)称为Between-class scatter matrix。
那么J(w)最终可以表示为：
\[J(w)=\frac{w^TS_Bw}{w^TS_Ww}\]在我们求导之前，需要对分母进行归一化，因为不做归一化的话，w扩大任何倍，公式都成立，我们就无法确定w。因此，我们打算令\(\|w^TS_Ww\|=1\)，那么加入拉格朗日乘子后，求导：
\[\begin{array}\\ c(w)=w^TS_Bw-\lambda(w^TS_Ww-1)\Rightarrow \frac{\text{d}c}{\text{d}w}=2S_Bw-2\lambda S_Ww=0\\ \Rightarrow S_Bw=\lambda S_Ww\Rightarrow S_W^{-1}S_Bw=\lambda w \end{array}\]可见，w实际上就是矩阵\(S_W^{-1}S_B\)的特征向量。
因为：
\[S_Bw=(\mu_1-\mu_2)(\mu_1-\mu_2)^Tw\]其中，后面两项的积是一个常数，记做\(\lambda_w\)，则：
\[S_W^{-1}S_Bw=S_W^{-1}(\mu_1-\mu_2)\lambda_w=\lambda w\]由于对w扩大缩小任何倍不影响结果，因此可以约去两边的未知常数\(\lambda,\lambda_w\)，得到：
\[w=S_W^{-1}(\mu_1-\mu_2)\]至此，我们只需要求出原始样本的均值和方差就可以求出最佳的方向w。
上述结论虽然来自2维，但对于多维也是成立的。大特征值所对应的特征向量分割性能最好。由于\(S_W^{-1}S_B\)不一定是对称阵，因此得到的K个特征向量不一定正交，这也是与PCA不同的地方。
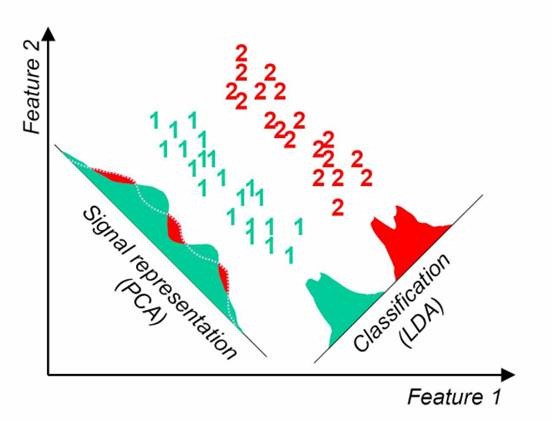
PCA选择样本点投影具有最大方差的方向，LDA选择分类性能最好的方向。
使用LDA的一些限制：
1.LDA至多可生成C-1维子空间。C为类别数。
LDA降维后的维度区间在[1,C-1]，与原始特征数n无关，对于二值分类，最多投影到1维。
2.LDA不适合对非高斯分布样本进行降维。
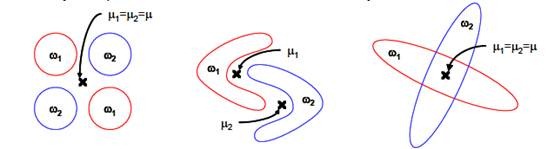
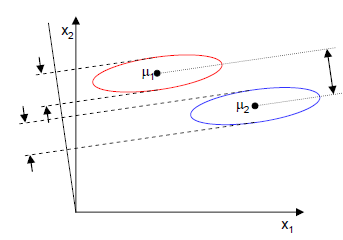
上图中红色区域表示一类样本，蓝色区域表示另一类，由于是2类，所以最多投影到1维上。不管在直线上怎么投影，都难使红色点和蓝色点内部凝聚，类间分离。
3.LDA在样本分类信息依赖方差而不是均值时，效果不好。
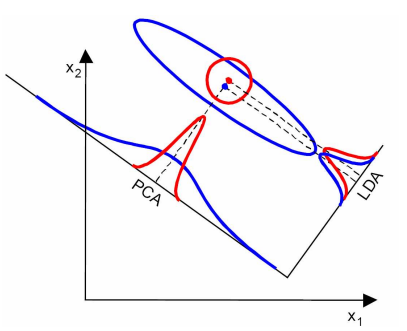
上图中，样本点依靠方差信息进行分类，而不是均值信息。LDA不能够进行有效分类，因为LDA过度依靠均值信息。
对LDA稍加扩展就得到了《图像处理理论（一）》中的Otsu法。Otsu法实际上是一维离散域的LDA。
此外，对于二值分类问题，最小二乘法和Fisher线性判别分析是一致的。
参考：
https://mp.weixin.qq.com/s/u-6nPrb4r9AS2gtrl5s-FA
LDA(Linear Discriminant Analysis)算法介绍
http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html
线性判别分析（Linear Discriminant Analysis）（一）
http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024389.html
线性判别分析（Linear Discriminant Analysis）（二）
https://mp.weixin.qq.com/s/AeLwfmM0N-b1dfxt3v4C-A
教科书上的LDA为什么长这样？
https://zhuanlan.zhihu.com/p/84660707
线性判别分析
