ML » 机器学习(三十二)——t-SNE
2018-01-20 :: 6005 WordsCRF
CRF的训练和推断(续)
- 学习问题
给定训练数据集X和对应的标记序列Y,K个特征函数\(f_k(x,y)\),需要学习linear-CRF的模型参数\(w_k\)和条件概率\(P_w(y\mid x)\)。(梯度下降法,牛顿法,拟牛顿法,迭代尺度法)
CRF/MEMM由于是判别模型,其训练过程和普通分类问题一致,没有特别之处。
CRF/MEMM的推断仍然使用Viterbi算法,选择最大概率路径即可。区别仅在于两者计算概率的公式不同,这在上文已有讨论,不再赘述。
相关工具
http://www.chokkan.org/software/crfsuite/
CRFsuite: A fast implementation of Conditional Random Fields (CRFs)
https://github.com/scrapinghub/python-crfsuite
A python binding for crfsuite
http://taku910.github.io/crfpp/
CRF++: Yet Another CRF toolkit
https://zhuanlan.zhihu.com/p/78006020
NCRF++学习笔记
参考
https://zhuanlan.zhihu.com/p/35969159
如何轻松愉快的理解条件随机场(CRF)?
https://www.cnblogs.com/en-heng/p/6214023.html
条件随机场CRF
https://mp.weixin.qq.com/s/1rx_R1BGRVAIDqKixNLMQA
终极入门 马尔可夫网络 (Markov Networks)——概率图模型
https://mp.weixin.qq.com/s/GXbFxlExDtjtQe-OPwfokA
一文轻松搞懂-条件随机场CRF
https://mp.weixin.qq.com/s/0FIns5Xt2G1seqFbpGvzTQ
长文详解基于并行计算的条件随机场
https://blog.csdn.net/liuyuemaicha/article/details/73147548
从PGM到HMM再到CRF
https://mp.weixin.qq.com/s/4r4k6JIj4xvHHmt3QqmbuA
以RNN形式做CRF后处理—CRFasRNN
https://mp.weixin.qq.com/s/JsqhwwJ7wnNcgOuAR6ekxw
理解条件随机场
https://mp.weixin.qq.com/s/79M6ehrQTiUc0l_sO9fUqA
用于序列标注问题的条件随机场(Conditional Random Field, CRF)
https://zhuanlan.zhihu.com/p/91031332
用腻了CRF,试试LAN吧?
https://zhuanlan.zhihu.com/p/100576406
条件随机场及Mininum Risk Training
https://www.jianshu.com/p/55755fc649b1
如何轻松愉快地理解条件随机场(CRF)?
https://zhuanlan.zhihu.com/p/34261803
白话条件随机场(conditional random field)
https://mp.weixin.qq.com/s/K-J4hbPpl8RQtpu1X6k1QQ
CRF原理及实现代码
https://mp.weixin.qq.com/s/PBfopbgkPyv4RbR-Lp0aWQ
逻辑回归与条件随机场
https://mp.weixin.qq.com/s/aWeS_E5qN27dtNbVWKtovw
使用条件随机场(CRF)来提升图像分割的表现
BiLSTM+CRF
上文已经提到CRF/MEMM中,有个概念叫做特征函数。和其他机器学习算法一样,这里的特征函数也是和领域相关的,并没有一个通用的做法。
DL兴起之后,一个很自然的想法就是,我们能不能用神经网络来作为特征函数呢?于是就有了BiLSTM+CRF:
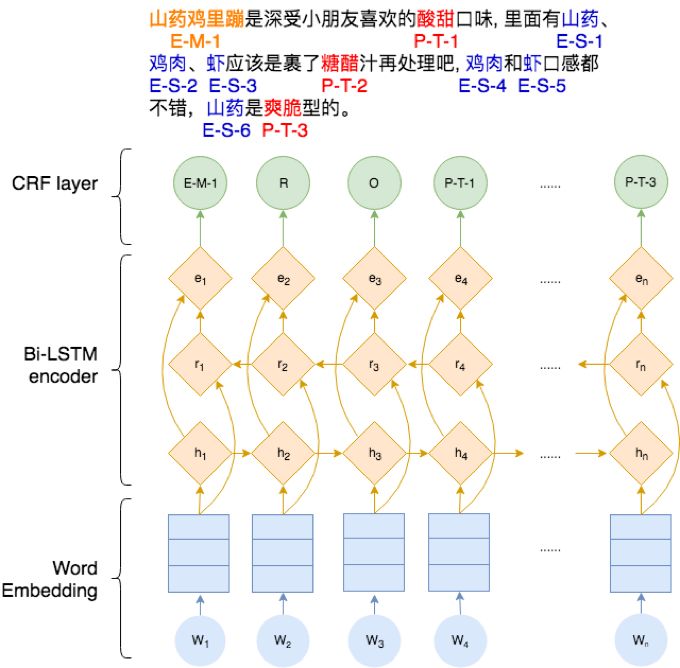
这里使用BiLSTM来提取序列特征,用CRF来预测label。
https://mp.weixin.qq.com/s/vbBNYzKq6AnsDTy8lFsKAw
TensorFlow RNN深度学习BiLSTM+CRF实现sequence labeling序列标注
https://www.jianshu.com/p/97cb3b6db573
BiLSTM模型中CRF层的运行原理-1
https://www.jianshu.com/p/7c83478eeb56
BiLSTM模型中CRF层的运行原理-2
https://www.zhihu.com/question/62399257
如何理解LSTM后接CRF?
https://mp.weixin.qq.com/s/1FCWMRapGMXjxTLoA2fYCg
CRF和LSTM模型在序列标注上的优劣?
https://zhuanlan.zhihu.com/p/97676647
手撕BiLSTM-CRF
https://zhuanlan.zhihu.com/p/44042528
最通俗易懂的BiLSTM-CRF模型中的CRF层介绍
https://mp.weixin.qq.com/s/0WVqQkvzb6TYFA9gEh73ZQ
BiLSTM上的CRF,用命名实体识别任务来解释CRF(1)
https://mp.weixin.qq.com/s/VG5C9NFMejetrj60KIbWug
BiLSTM上的CRF,用命名实体识别任务来解释CRF(2)损失函数
https://mp.weixin.qq.com/s/PaunoXYUz13s0lbgzcqE9A
BiLSTM上的CRF,用命名实体识别任务来解释CRF(3)推理
https://mp.weixin.qq.com/s/xJ7MpUkVfLQKxRYyJs29NQ
BiLSTM上的CRF,用命名实体识别任务来解释CRF(4)
https://mp.weixin.qq.com/s/LszJDl3x6kYQOd-p_FTx0g
BiLSTM+CRF命名实体识别:达观杯败走记(下篇)
t-SNE
概述
t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法,是由Laurens van der Maaten和Geoffrey Hinton在08年提出来。此外,t-SNE是一种非线性降维算法,非常适用于高维数据降维到2维或者3维,进行可视化。
论文:
《Visualizing Data using t-SNE》
以下是几种常见的降维算法:
1.主成分分析(线性)
2.t-SNE(非参数/非线性)
3.萨蒙映射(非线性)
4.等距映射(非线性)
5.局部线性嵌入(非线性)
6.规范相关分析(非线性)
7.SNE(非线性)
8.最小方差无偏估计(非线性)
9.拉普拉斯特征图(非线性)
PCA的相关内容参见《机器学习(十六)》。
SNE
在介绍t-SNE之前,我们首先介绍一下SNE(Stochastic Neighbor Embedding)的原理。
假设我们有数据集X,它共有N个数据点。每一个数据点\(x_i\)的维度为D,我们希望降低为d维。在一般用于可视化的条件下,d的取值为2,即在平面上表示出所有数据。
SNE将数据点间的欧几里德距离转化为条件概率来表征相似性:
\[p_{j\mid i}=\frac{\exp(-\|x_i-x_j\|^2/2\sigma^2)}{\sum_{k\neq i}\exp(-\|x_i-x_k\|^2/2\sigma^2)}\]如果以数据点在\(x_i\)为中心的高斯分布所占的概率密度为标准选择近邻,那么\(p_{j\mid i}\)就代表\(x_i\)将选择\(x_j\)作为它的近邻。对于相近的数据点,条件概率\(p_{j\mid i}\)是相对较高的,然而对于分离的数据点,\(p_{j\mid i}\)几乎是无穷小量(若高斯分布的方差\(\sigma_i\)选择合理)。
现在引入矩阵Y,Y是N*2阶矩阵,即输入矩阵X的2维表征。基于矩阵Y,我们可以构建一个分布q,其形式与p类似。
对于高维数据点\(x_i\)和\(x_j\)在低维空间中的映射点\(y_i\)和\(y_j\),计算一个相似的条件概率\(q_{j\mid i}\)是可以实现的。我们将计算条件概率\(q_{i\mid j}\)中用到的高斯分布的方差设置为1/2。因此我们可以对映射的低维数据点\(y_j\)和\(y_i\)之间的相似度进行建模:
\[q_{j\mid i}=\frac{\exp(-\|y_i-y_j\|^2)}{\sum_{k\neq i}\exp(-\|y_i-y_k\|^2)}\]我们的总体目标是选择Y中的一个数据点,然后其令条件概率分布q近似于p。这一步可以通过最小化两个分布之间的KL散度而实现,这一过程可以定义为:
\[C = \sum_i KL(P_i \| Q_i) = \sum_i \sum_j p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}\]这里的\(P_i\)表示了给定点\(x_i\)下,其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性,在低维映射中不同的距离对应的惩罚权重是不同的,具体来说:距离较远的两个点来表达距离较近的两个点会产生更大的cost,相反,用较近的两个点来表达较远的两个点产生的cost相对较小(注意:类似于回归容易受异常值影响,但效果相反)。即用较小的\(q_{j\mid i}=0.2\)来建模较大的\(p_{j\mid i}=0.8\),\(cost=p\log(p/q)=1.11\),同样用较大的\(q_{j\mid i}=0.8\)来建模较小的\(p_{j\mid i}=0.2\),\(cost=-0.277\)。因此,SNE会倾向于保留数据中的局部特征。
如何确定\(\sigma\)
下面介绍一下SNE的超参\(\sigma\)的确定方法。
首先,不同的点具有不同的\(\sigma_i\),\(P_i\)的熵(entropy)会随着\(\sigma_i\)的增加而增加。SNE使用困惑度(perplexity)的概念,用二分搜索的方式来寻找一个最佳的\(\sigma\)。其中困惑度指:
\[Perp(P_i) = 2^{H(P_i)}\]这里的\({H(P_i)}\)是\(P_i\)的熵,即:
\[H(P_i) = -\sum_j p_{j \mid i} \log_2 p_{j \mid i}\]困惑度可以解释为一个点附近的有效近邻点个数。SNE对困惑度的调整比较有鲁棒性,通常选择5-50之间。
在初始优化的阶段,每次迭代中可以引入一些高斯噪声,之后像模拟退火一样逐渐减小该噪声,可以用来避免陷入局部最优解。因此,SNE在选择高斯噪声,以及学习速率,什么时候开始衰减,动量选择等等超参数上,需要跑多次优化才可以。
Symmetric SNE
优化\(p_{i \mid j}\)和\(q_{i \mid j}\)的KL散度的一种替换思路是,使用联合概率分布来替换条件概率分布,即P是高维空间里各个点的联合概率分布,Q是低维空间里各个点的联合概率分布,目标函数为:
\[C = KL(P \mid \mid Q) = \sum_i \sum_j p_{i,j} \log \frac{p_{ij}}{q_{ij}}\]如果我们假设对于任意i,有\(p_{ij} = p_{ji}, q_{ij} = q_{ji}\),则概率分布可以改写为:
\[p_{ij} = \frac{\exp(- \mid \mid x_i - x_j \mid \mid ^2 / 2\sigma^2)}{\sum_{k \neq l} \exp(- \mid \mid x_k-x_l \mid \mid ^2 / 2\sigma^2)} \ \ \ \ q_{ij} = \frac{\exp(- \mid \mid y_i - y_j \mid \mid ^2)}{\sum_{k \neq l} \exp(- \mid \mid y_k-y_l \mid \mid ^2)}\]我们将这种SNE称之为symmetric SNE(对称SNE)。
t-SNE
SNE的主要问题在于存在Crowding问题:就是说各个簇聚集在一起,无法区分。比如有一种情况,高维度数据在降维到10维下,可以有很好的表达,但是降维到两维后无法得到可信映射,比如降维如10维中有11个点之间两两等距离的,在二维下就无法得到可信的映射结果(最多3个点)。
其中的一种减轻”拥挤问题”的方法:在高维空间下,在高维空间下我们使用高斯分布将距离转换为概率分布,在低维空间下,我们使用更加偏重长尾分布的方式来将距离转换为概率分布,使得高维度下中低等的距离在映射后能够有一个较大的距离。
我们对比一下高斯分布和t分布, t分布受异常值影响更小,拟合结果更为合理,较好的捕获了数据的整体特征。
使用了t分布之后的q变化,如下:
\[q_{ij} = \frac{(1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}{\sum_{k \neq l} (1 + \mid \mid y_i -y_j \mid \mid ^2)^{-1}}\]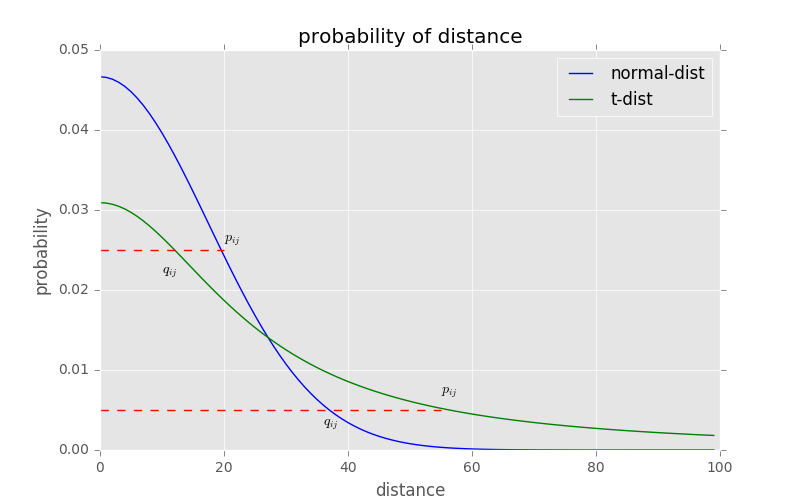
t-sne的有效性,也可以从上图中看到:横轴表示距离,纵轴表示相似度, 可以看到,对于较大相似度的点,t分布在低维空间中的距离需要稍小一点;而对于低相似度的点,t分布在低维空间中的距离需要更远。这恰好满足了我们的需求,即同一簇内的点(距离较近)聚合的更紧密,不同簇之间的点(距离较远)更加疏远。
总结一下,t-SNE的梯度更新有两大优势:
对于不相似的点,用一个较小的距离会产生较大的梯度来让这些点排斥开来。
这种排斥又不会无限大(梯度中分母),避免不相似的点距离太远。

您的打赏,是对我的鼓励
