Antkillerfarm Hacking V7.5

ML » 机器学习（三十一）——MRF, CRF

2018-01-09 :: 4847 Words

HMM

前向算法（续）

穷举法的计算量太大，不适用于计算较长的马尔可夫链。但是我们可以观察一下穷举法的计算步骤。

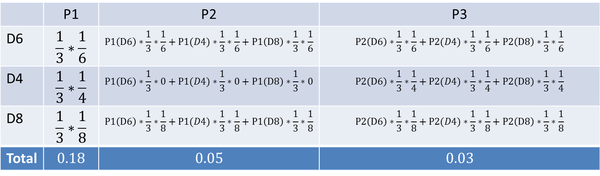
上图是某骰子序列的穷举计算过程，可以看出第3步计算的概率和公式的某些项，实际上在之前的步骤中已经计算出来了，前向递推的计算量并没有想象中的大。

Baum–Welch算法

Baum–Welch算法是求解问题3的常用算法，由Baum和Welch于1972年提出。它虽然是EM算法的一个特例，但后者却是1977年才提出的。

Leonard Esau Baum，1931～2017，美国数学家，哈佛博士（1958）。国防分析研究所研究员，70年代末，加盟对冲基金——文艺复兴科技公司。

Lloyd Richard Welch，生于1927年，美国数学家，加州理工博士（1958），南加州大学教授。美国工程院院士，Shannon Award获得者（2003）。

Baum–Welch算法也叫前向后向算法。因为它包含了前向和后向两个步骤。

  1. expectation：计算隐变量的概率分布，并得到可观察变量与隐变量联合概率的log-likelihood在前面求得的隐变量概率分布下的期望。这个步骤就是所谓的前向步骤，算法和求解问题2的forward算法是一致的

  2. maximization：求得使上述期望最大的新的模型参数。若达到收敛条件则退出，否则回到步骤1。

前向后向算法则主要是解决Expectation这步中求隐变量概率分布的一个算法，它利用dynamic programming大大减少了计算量。

此外，训练HMM模型时，也需要对模型参数进行随机初始化，不然和神经网络一样，由于参数没有差异性，而无法进行训练。

参考：

https://blog.csdn.net/xmu_jupiter/article/details/50965039

HMM的Baum-Welch算法和Viterbi算法公式推导细节

HMM在NLP领域的应用

具体到分词系统，可以将“标签”当作隐含状态，“字或词”当作可见状态。那么，几个NLP的问题就可以转化为：

词性标注：给定一个词的序列（也就是句子），找出最可能的词性序列（标签是词性）。如ansj分词和ICTCLAS分词等。

分词：给定一个字的序列，找出最可能的标签序列（断句符号：[词尾]或[非词尾]构成的序列）。结巴分词目前就是利用BMES标签来分词的，B（开头）,M（中间),E(结尾),S(独立成词）

命名实体识别：给定一个词的序列，找出最可能的标签序列（内外符号：[内]表示词属于命名实体，[外]表示不属于）。如ICTCLAS实现的人名识别、翻译人名识别、地名识别都是用同一个Tagger实现的。

综上，在监督学习中，一般把训练数据当作HMM的可见状态，而把标签当作隐含状态。当然这里的标签一般是生成最终训练标签的一个概率模型的参数。

如果标签不是概率模型的，而是已知确定的话，那么就退化为普通的逻辑回归，直接用极大似然估计即可。

正由于标签是概率模型的，存在一个建模的过程，因此HMM实际上是一种生成模型算法。

HMM只遵循了一阶马尔科夫假设，即1-gram。如果数据的依赖超过1-gram，则不能使用HMM，而需要使用高阶HMM。

参考：

http://blog.sina.com.cn/s/blog_8267db980102wq4l.html

HMM识别新词

https://mp.weixin.qq.com/s/eGx0PHvZXwmykUon-9M-mQ

HMM模型在贝壳对话系统中的应用

https://www.cnblogs.com/en-heng/p/6183522.html

二阶隐马尔可夫模型2-HMM

MRF

前文已经指出无向的概率图模型也叫做Markov Random Field。

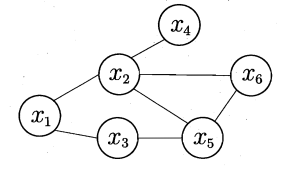
上图是一个简单的MRF的示意图。无向图的边没有箭头，表示变量之间是相互依赖的。

对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个团（clique）。

若在一个团中，加入另外任何一个结点都不能形成团，则称该团为极大团（maximal clique）。

上图中，\(\{x_5,x_6\}\)是团，\(\{x_2,x_5,x_6\}\)是极大团，而\(\{x_1,x_2,x_3\}\)不是团，因为\(x_2,x_3\)之间没有连接。

从团的定义可以看出：

  • 无法组团的两个结点之间由于没有依赖关系，因此是相互独立的。

  • 每个结点至少出现在一个极大团中。孤立结点的极大团就是它本身。

  • 若Q不是一个极大团，则必有极大团Q*包含Q。

基于以上性质，我们效仿整数的因子分解，提出了概率图的极大团分解：

\[P(x)=\frac{1}{Z^*}\prod_{Q\in C^*}\psi_Q(x_Q)\tag{1}\]

其中，\(\psi_Q\)为Q对应的势函数。

\[Z^*=\sum_x \prod_{Q\in C^*} \psi_Q(x_Q)\]

\(Z^*\)通常被称为规范化因子，用于使输出符合概率的定义（部分概率\(\le 1\)，全概率\(=1\)）。

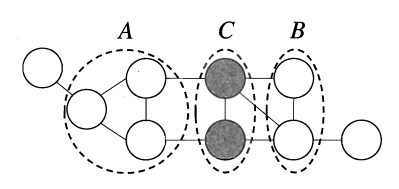
如上图所示，结点集A中的结点到B中的结点，必须经过C中的结点，则称A和B被C分离，C称为分离集（separating set）。

显然，A和B由于没有直接关系，因此是相对于C条件独立的。这就是所谓的global Markov property。即：

\[P(x_A,x_B|x_C)=P(x_A|x_C)P(x_B|x_C)\]

从结点间的连通性上，还可得以下术语：

马尔可夫毯(Markov Blanket, MB)：有向图——结点A的父结点+A的子结点+A的子结点的其他父结点。如下图所示：

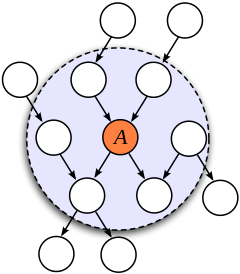
无向图——结点A的邻接结点。

和global Markov property类似，还有local Markov property：给定某变量的邻接变量，则该变量条件独立于其他变量。

MEMM

Maximum Entropy Markov Model是一种判别模型。它和HMM的联系和区别主要表现在以下方面：

  • 生成 vs 判别

正如《机器学习（三）》中提到的，MEMM既然是判别模型，那它实际上就是一个确定决策边界的分类问题。分类问题使用Maximum Entropy建模就是一件很自然的事情了。

单纯的ME，由于没有利用历史信息，对于序列问题的效果并不好。因此，仿照HMM，又引入了Markov Model，这也就是MEMM得名的原因。

我们回过头来，再看《机器学习（三十）》中的这张图：

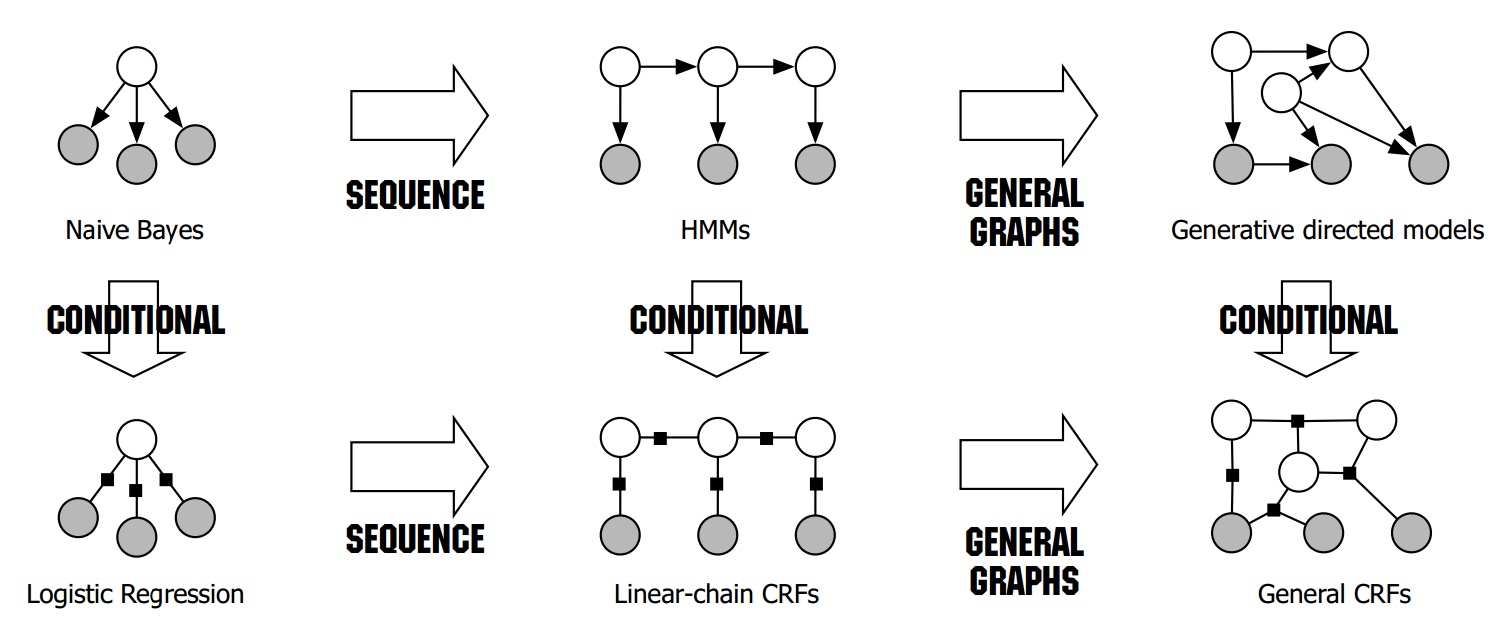
显然，如果考虑历史信息的话，Naive Bayes就变成了HMMs，同理，LR就变成了CRF。（MEMM和CRF在这一点上是一致的）

  • 概率图表示

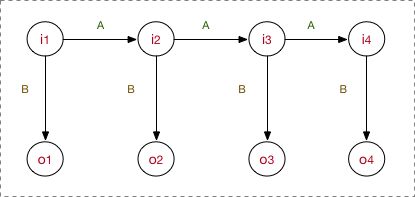
上图是HMM的概率图表示。其中，i表示状态节点，o表示观测节点。从中可以看出，\(o_t\)的状态，只取决于\(i_t\)，而\(i_t\)的状态，只取决于\(i_{t-1}\)的状态。

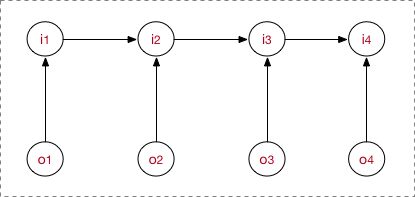
上图是MEMM的概率图表示。MEMM当前隐藏状态\(i_t\)依赖于当前时刻的观测节点\(o_t\)和上一时刻的隐藏节点\(i_{t-1}\)。

  • 特征建模

HMM的建模实际上是比较简单的了，主要就是状态转移概率矩阵和观测概率矩阵。这些都是一阶线性的特征了。

MEMM不局限于这样的简单特征，你可以用任意复杂的方式定义特征。一般将特征函数表示为：\(f_a(i,o)\)。其中，a表示特征。一个MEMM模型可以包含任意多个特征。

综上，我们可以给出MEMM的公式：

\[P(I|O)=\prod_{t=1}^n\frac{\exp(\sum_a \lambda_a f_a(i,o))}{Z(i,o)}\tag{2}\]

其中Z为归一化因子：\(Z=\sum_i \exp(\sum_a \lambda_a f_a(i,o))\)

这里的\(\lambda_a\)就是模型需要学习的参数。

MEMM存在labeling bias问题。

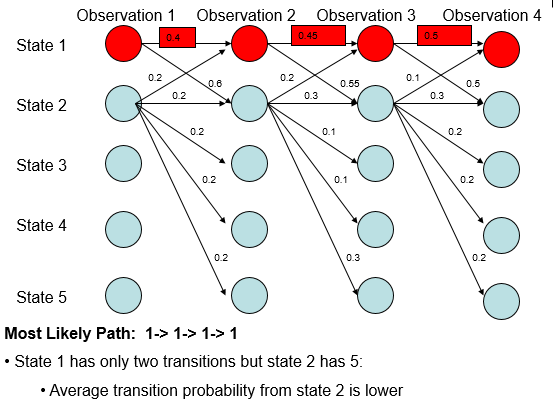
如上面的例子，可以看出：

  • 无论观测值，State 1总是更倾向于转移到State 2；

  • 无论观测值，State 2总是更倾向于转移到State 2；

因此，无论初值如何，Most Likely Path最终待在State 2中，才是合理的。然而MEMM却认为待在State 1中才合理。

产生这种现象的原因是，State 1有2个转移方式，而State 2有5个转移方式。这就导致尽管State 1->State 1是小概率事件，但也比State 2的任意一个转移事件的概率大。谁叫后者的概率这么分散呢？

参考：

http://www.cnblogs.com/en-heng/p/6201893.html

中文分词：最大熵马尔可夫模型MEMM

http://www.cnblogs.com/549294286/archive/2013/06/06/3121761.html

统计模型之间的比较，HMM，最大熵模型，CRF条件随机场

http://blog.csdn.net/caohao2008/article/details/4242308

HMM,MEMM,CRF模型的比较

http://blog.csdn.net/zhoubl668/article/details/7787690

标注偏置问题(Label Bias Problem)和HMM、MEMM、CRF模型比较

http://tripleday.cn/2016/07/14/hmm-memm-crf/

HMM、MEMM和CRF的学习总结

https://zhuanlan.zhihu.com/p/33397147

概率图模型体系：HMM、MEMM、CRF

CRF

概述

条件随机场(Conditional Random Field)由Lafferty等人于2001年提出，结合了最大熵模型和隐马尔可夫模型的特点，是一种无向图模型，近年来在分词、词性标注和命名实体识别等序列标注任务中取得了很好的效果。

上面我们为了解释HMM和MEMM的区别，对MEMM做了一定的简化，事实上MEMM还可以是这样的：

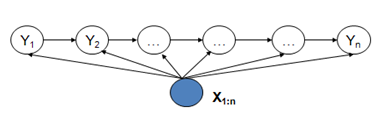
这表明，MEMM可以利用观测序列的全序列信息，而不仅仅是当前的观测值。至于MEMM的隐藏状态，则还是只依赖上一个隐藏状态。

CRF是一种特殊的MRF。MRF定义的是联合概率，而CRF定义的是条件概率，故名。

在CRF中，最常用的是Linear-chain CRF。

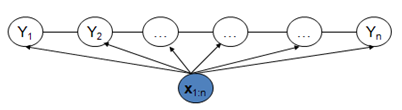
Linear-chain CRF和MEMM类似，也对隐藏状态的依赖进行了约束：只依赖上一个隐藏状态。

有的时候，Linear-chain CRF也被不加区分的简称为CRF。下文如无特指，CRF均指的是Linear-chain CRF，它的概率图如下所示：

根据MRF的公式（公式1）和MEMM的公式（公式2），我们可以得到CRF的公式如下：

\[P(I|O)=\frac{\prod_{t=1}^n\exp(\sum_a \lambda_a f_a(i,o))}{Z(i,o)}\]

由于Z位置的不同，CRF的概率是全局归一化的，而MEMM是局部归一化的，因此CRF没有labeling bias的问题。

CRF的训练和推断

与HMM类似，CRF也有三个基本问题：

  • 计算问题

给定条件随机场\(P(Y\mid X)\)，输入序列x和输出序列y，计算条件概率和以及对应的期望。（前向后向算法）

  • 解码问题

给定条件随机场\(P(Y\mid X)\)和输入序列x，求条件概率最大的输出序列y，即对观测序列进行标注。（维特比算法）

Antkillerfarm
antkillerfarm@sohu.com

github.com/antkillerfarm

Fork me on GitHub