ML » 机器学习(二十九)——在线学习, 贝叶斯学习, Beam Search, 集成学习
2017-11-19 :: 5698 Words在线学习
我们之前讨论的算法,都是给定一个训练集S,经训练之后,得到预测函数h,然后再在新的样本集上进行预测。这种方法被称为批量学习(batch learning)。
与之相对的,还有一种边学习边预测的在线学习(online learning)算法。其步骤如下:
1.\(i:=0\)。
2.输入\(x^{(i)}\),算法预测\(y^{(i)}\)。
3.根据\(y^{(i)}\)的真实值,修正算法模型。这一步也被称作更新过程(update procedure)
4.令\(i:=i+1\),以处理下一个数据样本。
在线学习的优点: 1.算法在学习过程中,即可预测。 2.随着数据样本的增多,预测会更加准确,即具有自我完善的的能力。
下面以感知器(perceptron)算法为例,讨论一下在线学习的误差问题。
首先回忆一下感知器算法:
\[h_\theta(x)=g(\theta^Tx),y\in\{1,-1\}\] \[g(z)=\begin{cases} 1, & z\ge 0 \\ -1, & z<0 \\ \end{cases}\]对于训练样本\((x,y)\),其更新过程为:
\[\theta:=\begin{cases} \theta, & h_\theta(x)=y \\ \theta+yx, & otherwise \\ \end{cases}\tag{3}\]这里给出一个和感知器算法有关的定理:
对于给定的m个样本序列(注意“序列”二字,在线算法对于样本的顺序是敏感的)\(x^{(i)}\),如果所有的\(\|x^{(i)}\|\le D\),并且存在单位向量u,使得所有样本的\(y^{(i)}(u^Tx^{(i)})\ge \gamma\),则感知器算法在该序列上的预测错误个数最多为\((D/\gamma)^2\)。
这个定理是Henry David Block和Albert B. J. Novikoff于1962年提出的。
Henry David Block,1920~1978,美国数学家。
这个人的经历有点非典型。20岁本科毕业,由于专业是文学和心理学,结果找不到工作。只好回炉,又读了个土木工程的本科。
二战期间在Goodyear的飞机工厂(没错,就是那个卖轮胎的Goodyear)担任测试工程师。在那里碰到一个当医生的英国妹子,搞定之。
1946年,他老婆在Iowa State University获得了一个职位,于是他也跟着搬了过去。估计是无所事事,他经常到大学里蹭课,然后就发现自己对数学很感兴趣。
于是继续读书,1949年拿到博士学位。经过几年助教生涯之后,最终成为康奈尔大学应用数学教授。
话说,根据缩写找人真是太痛苦了,很多资料都不是你要找的人,Block又是个大路货。我最后是在他的一位同事的论文中找到他的全名的。那篇论文发表于1985年,距离他去世已经7年,但他仍是作者之一,可见人缘不错。
Albert B. J. Novikoff,全名不详,只知道是纽约大学教授。从岁数来看应该已经退休了。
下面给出这个定理的证明过程:
由公式3可知,\(\theta\)的值只有在发生预测错误的时候才会改变,因此我们可以使用\(\theta^{(k)}\)表示第k个错误。同时令\(\theta^1=0\)。
根据更新公式可得:
\[(\theta^{(k+1)})^Tu=(\theta^{(k)})^Tu+y^{(i)}(x^{(i)})^Tu\ge (\theta^{(k)})^Tu+\gamma\]所以:
\[(\theta^{(2)})^Tu\ge (\theta^{(1)})^Tu+\gamma=\gamma\] \[(\theta^{(3)})^Tu\ge (\theta^{(2)})^Tu+\gamma\ge 2\gamma\]由数学归纳法可得:
\[(\theta^{(k+1)})^Tu\ge k\gamma\tag{4}\]另外,
\[\|\theta^{(k+1)}\|^2=\|\theta^{(k)}+y^{(i)}x^{(i)}\|^2=\|\theta^{(k)}\|^2+\|y^{(i)}x^{(i)}\|^2+2y^{(i)}(x^{(i)})^T\theta^{(k)}\]由感知器算法的定义可得:
\[y^{(i)}(x^{(i)})^T\theta^{(k)}\le 0\]所以:
\[\|\theta^{(k+1)}\|^2\le \|\theta^{(k)}\|^2+\|x^{(i)}\|^2\le \|\theta^{(k)}\|^2+D^2\]同样,由数学归纳法可得:
\[\|\theta^{(k+1)}\|^2\le kD^2\tag{5}\]因为:
\[(\theta^{(k+1)})^Tu=\|\theta^{(k+1)}\|\cdot\|u\|\cdot \cos\phi\le \|\theta^{(k+1)}\|\cdot\|u\|=\|\theta^{(k+1)}\|\tag{6}\]由公式4、5、6可得:
\[\sqrt{k}D\ge \|\theta^{(k+1)}\|\ge (\theta^{(k+1)})^Tu\ge k\gamma\]所以:
\[k\le (D/\gamma)^2\]参考:
https://zhuanlan.zhihu.com/p/75597761
如何增强推荐系统模型更新的“实时性”?
贝叶斯学习
1787年5月,美国各州(当时为13个)代表在费城召开制宪会议;1787年9月,美国的宪法草案被分发到各州进行讨论。一批反对派以“反联邦主义者”为笔名,发表了大量文章对该草案提出批评。宪法起草人之一亚历山大·汉密尔顿着急了,他找到曾任外交国务秘书(即后来的国务卿)的约翰·杰伊,以及纽约市国会议员麦迪逊,一同以普布利乌斯(Publius)的笔名发表文章,向公众解释为什么美国需要一部宪法。他们走笔如飞,通常在一周之内就会发表3-4篇新的评论。1788年,他们所写的85篇文章结集出版,这就是美国历史上著名的《联邦党人文集》。
《联邦党人文集》出版的时候,汉密尔顿坚持匿名发表,于是,这些文章到底出自谁人之手,成了一桩公案。1810年,汉密尔顿接受了一个政敌的决斗挑战,但出于基督徒的宗教信仰,他决意不向对方开枪。在决斗之前数日,汉密尔顿自知时日不多,他列出了一份《联邦党人文集》的作者名单。1818年,麦迪逊又提出了另一份作者名单。这两份名单并不一致。在85篇文章中,有73篇文章的作者身份较为明确,其余12篇存在争议。
像这样一个问题,在没有机器学习的时代,可以耗费一个考据学家10年20年也不一定能有结果。但是用机器学习一个叫朴素贝叶斯的方法,就可以解开。
https://mp.weixin.qq.com/s/szTmHY-Yvn7N3s_GzTDiEA
解开贝叶斯黑暗魔法:通俗理解贝叶斯线性回归
https://mp.weixin.qq.com/s/1JSxjkKEUlWOzXCQPTve3A
贝叶斯线性回归简介
https://mp.weixin.qq.com/s/NTK-u4aVrTTmvi-4ZBa8RQ
数十亿用户的Facebook如何进行贝叶斯系统调优?
https://mp.weixin.qq.com/s/g24mcZjQ25sQJx9mqE_XSA
怎样判断漂亮女孩是不是单身的?美国海军在汪洋大海里搜索丢失的氢弹、失踪的核潜艇都用过这种方法。
https://mp.weixin.qq.com/s/bjyO4AS1Sjo09qNMpqf6JA
最新36页《贝叶斯非参学习综述》,机器学习内功修炼手册
https://mp.weixin.qq.com/s/x3AREJcDKvjo7vl6TS79OA
贝叶斯推理实用入门
https://mp.weixin.qq.com/s/Tk2t3R_SUU6S9yvdjnwzDQ
量化交易中的贝叶斯优化问题
https://mp.weixin.qq.com/s/1JH3hDy0FXUjGB4QgTd31g
不看任何数学公式来讲解贝叶斯算法
https://zhuanlan.zhihu.com/p/59196946
如何用贝叶斯高斯张量分解修复缺失数据?
https://zhuanlan.zhihu.com/p/63351454
如何用贝叶斯概率矩阵分解修复缺失数据?
https://mp.weixin.qq.com/s/GuM0jZlI4mC-DFSWybtG1A
贝叶斯优化简介
https://mp.weixin.qq.com/s/YtSYiw23J3oTXUXwNeoIEg
一文读懂贝叶斯优化
https://mp.weixin.qq.com/s/7GamrrteCUsePWStOuHbVw
贝叶斯推断随机过程,449页pdf
https://mp.weixin.qq.com/s/kqs5Gwr1XgldX-Yz2iJjzw
贝叶斯优化(Bayesian Optimization)
https://mp.weixin.qq.com/s/WPpAqLuisfN3za1LJpG6JQ
一文看懂贝叶斯优化/Bayesian Optimization
Beam Search
概述
Beam Search(集束搜索)是一种启发式图搜索算法,通常用在图的解空间比较大的情况下,为了减少搜索所占用的空间和时间,在每一步深度扩展的时候,剪掉一些质量比较差的结点,保留下一些质量较高的结点。保留下来的结点个数一般叫做Beam Width。
这样减少了空间消耗,并提高了时间效率,但缺点就是有可能存在潜在的最佳方案被丢弃,因此Beam Search算法是不完全的,一般用于解空间较大的系统中。
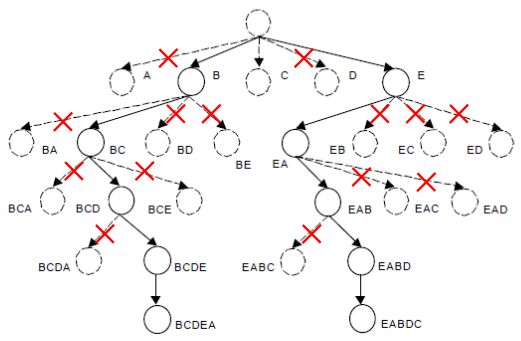
上图是一个Beam Width为2的Beam Search的剪枝示意图。每一层只保留2个最优的分支,其余分支都被剪掉了。
显然,Beam Width越大,找到最优解的概率越大,相应的计算复杂度也越大。因此,设置合适的Beam Width是一个工程中需要trade off的事情。
当Beam Width为1时,也就是著名的A*算法了。
https://mp.weixin.qq.com/s/R7oxzvlTZfyhtxc2wkgbWQ
你一直在用的Beam Search,是否真的有效?
Beam Search与Viterbi算法
Beam Search与Viterbi算法虽然都是解空间的剪枝算法,但它们的思路是不同的。
Beam Search是对状态迁移的路径进行剪枝,而Viterbi算法是合并不同路径到达同一状态的概率值,用最大值作为对该状态的充分估计值,从而在后续计算中,忽略历史信息(这种以偏概全也就是所谓的Markov性),以达到剪枝的目的。
从状态转移图的角度来说,Beam Search是空间剪枝,而Viterbi算法是时间剪枝。
参考
http://people.csail.mit.edu/srush/optbeam.pdf
Optimal Beam Search for Machine Translation
http://www.cnblogs.com/xxey/p/4277181.html
Beam Search(集束搜索/束搜索)
http://blog.csdn.net/girlhpp/article/details/19400731
束搜索算法(Andrew Jungwirth 初稿)BEAM Search
http://hongbomin.com/2017/06/23/beam-search/
Beam Search算法及其应用
https://mp.weixin.qq.com/s/GTtjjBgCDdLRwPrUqfwlVA
如何使用贪婪搜索和束搜索解码算法进行自然语言处理
https://mp.weixin.qq.com/s/7bpvoZykdAkHXwDL7-39Qw
十分钟读懂Beam Search(1/2)
https://mp.weixin.qq.com/s/BuvLXx0ZItOvhno4XAUpTg
十分钟读懂Beam Search(2/2)
https://mp.weixin.qq.com/s/HFXzBZtf6-s_IQpZvdQ8Tw
Beam Search、GREEDY DECODER、SAMPLING DECODER等解码器工作原理可视化
集成学习
https://mp.weixin.qq.com/s/hGoprRIeyoXPt5OnzgV-bg
集成学习算法(Ensemble Method)浅析
https://mp.weixin.qq.com/s/_rKnE833oPkRTUfkZGn7fQ
机器学习之集成学习
https://mp.weixin.qq.com/s/VgFnREuG_D6lbTvs3JLBHg
集成学习基础通俗入门
https://mp.weixin.qq.com/s/I41c-i-6y-pPdZOeiMM_0Q
通俗讲解集成学习算法!
https://mp.weixin.qq.com/s/z42pMRSOSt8GkOCRHcDtNg
集成深度学习在生物信息学中的应用
https://mp.weixin.qq.com/s/7RU3Nzy5qkTL8-2LOjg9qg
从基础到实现:集成学习综合教程
https://mp.weixin.qq.com/s/Pkc8KyDZ53ZGO5lNLVjoBg
一份完备的集成学习手册!
https://mp.weixin.qq.com/s/jQqSWEaxeUZ6UBeFZO7tJQ
机器学习集成学习与模型融合

您的打赏,是对我的鼓励
