ML » 机器学习（二十三）——训练集、验证集和测试集, Optimizer
2017-06-13 :: 6107 Words训练集、验证集和测试集
对于一个模型来说，其参数可以分为普通参数和超参数。在不引入强化学习的前提下，那么普通参数就是可以被梯度下降所更新的，也就是训练集所更新的参数。另外，还有超参数的概念，比如网络层数、网络节点数、迭代次数、学习率等等，这些参数不在梯度下降的更新范围内。尽管现在已经有一些算法可以用来搜索模型的超参数，但多数情况下我们还是自己人工根据验证集来调。
从狭义来讲，验证集没有参与梯度下降的过程，也就是说是没有经过训练的；但从广义上来看，验证集却参与了一个“人工调参”的过程，我们根据验证集的结果调节了迭代数、调节了学习率等等，使得结果在验证集上最优。因此，我们也可以认为，验证集也参与了训练。
那么就很明显了，我们还需要一个完全没有经过训练的集合，那就是测试集。
参考：
http://kexue.fm/archives/4638/
训练集、验证集和测试集的意义
https://zhuanlan.zhihu.com/p/48976706
训练集、验证集和测试集
https://mp.weixin.qq.com/s/idS2l7u_OBxWi5UBexlK4w
如何正确使用机器学习中的训练集、验证集和测试集？
https://mp.weixin.qq.com/s/ubpRPQ7-1nvY5CzICWi1Cg
似乎没区别，但你混淆过验证集和测试集吗？
Optimizer
在《机器学习（一）》中，我们已经指出梯度下降是解决凸优化问题的一般方法。而如何更有效率的梯度下降，就是本节中Optimizer的责任了。
教程
http://www.stat.cmu.edu/~ryantibs/convexopt/
Machine Learning 10-725: Convex Optimization
https://mp.weixin.qq.com/s/9BRhZd6x-JCNNVzt2ndYKQ
最新《深度学习优化问题》教程，78页ppt，台大林智仁教授讲解
原始版本
早期的梯度下降法一般用以下公式确定学习率：
\[\eta_t=\frac{\eta_0}{\sqrt{t+1}}\]Momentum
Momentum是梯度下降法中一种常用的加速技术。其公式为：
\[v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)\] \[\theta = \theta - v_t\]从上式可以看出，参数的更新值\(v_t\)，不仅取决于当前梯度\(\nabla_\theta J( \theta)\)，还取决于上一刻的速度\(v_{t-1}\)。
Nesterov accelerated gradient
该方法是Momentum的一个变种。其公式为：
\[v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1})\] \[\theta = \theta - v_t\]Yurii Nesterov，莫斯科大学应用数学系本科（1977年），凸优化理论专家。法国鲁汶天主教大学教授。2009年获John von Neumann Theory Prize。
参考：
https://zhuanlan.zhihu.com/p/22810533
比Momentum更快：揭开Nesterov Accelerated Gradient的真面目
https://zhuanlan.zhihu.com/p/27435669
从Nesterov的角度看：我们为什么要研究凸优化？
https://www.cs.cmu.edu/~ggordon/10725-F12/slides/09-acceleration.pdf
Accelerated first-order methods
Adagrad
Momentum算法中所有的参数\(\theta\)都使用同一个学习率，而Adagrad采用了另一种方法进行优化：为每个参数确定不同的学习率。
Adagrad的基本思想：给经常更新的参数一个较小的学习率，而给很少更新的参数一个较大的学习率。
其公式为：
\[g_{t, i} = \nabla_\theta J( \theta_i )\] \[\theta_{t+1, i} = \theta_{t, i} - \dfrac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i}\]其中，\(G_{t, ii}\)表示参数\(\theta_i\)梯度平方和的历史累积值，\(\epsilon\)是为了防止分母为0，而加入的平滑项，数量级一般为\(10^{-8}\)。
有趣的是，如果去掉上式中的根号，则其效果会变糟。
Adagrad的优点在于：它是一个自适应算法，初值选择显得不太重要了。
Adagrad的缺点在于：训练越往后，G越大，从而学习率越小。如果在训练完成之前，学习率变为0，就会导致提前结束训练。
Adadelta
为了克服Adagrad的缺点，Matthew D. Zeiler于2012年提出了Adadelta算法。
Matthew D. Zeiler，多伦多大学本科（2009）+纽约大学博士（2013）。Clarifai创始人和CEO。读书期间，他还创立了一家给大学生卖习题册的公司。
个人主页：
http://www.matthewzeiler.com/
该算法不再使用历史累积值，而是只取最近的w个状态，这样就不会让梯度被惩罚至0。
为了避免保存前w个状态的梯度平方和，可做如下变换：
\[E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t\] \[\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}\]上边的公式，就是Hinton在同一年提出的RMSprop算法。其中的\(\gamma E[g^2]_{t-1}\)即可看作是前w个状态的滤波值，也可看作是Momentum算法中动量值。
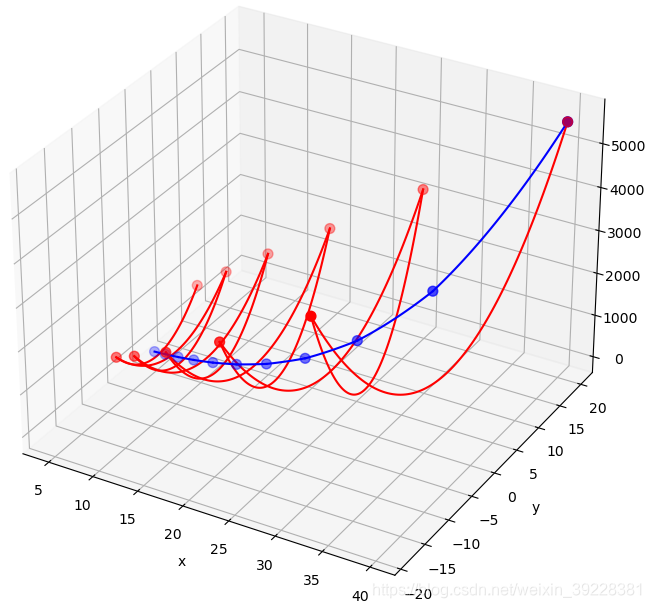
其中红色对应SGD，蓝色对应RMSProp。可以看出通过RMSProp，有效消除了梯度差异导致的抖动。
Adadelta在RMSprop的基础上更进一步：
\[RMS[g]_{t}=\sqrt{E[g^{2}]_{t}+\epsilon }\] \[\Delta \theta_t = - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t}\]也就是说，Adadelta不仅考虑了梯度的平方和，也考虑了更新量的平方和。
Adam
Adaptive Moment Estimation借用了卡尔曼滤波的思想，对\(g_t,g_t^2\)进行滤波：
\[m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\] \[v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\]估计：
\[\hat{m}_t = \dfrac{m_t}{1 - \beta^t_1}\] \[\hat{v}_t = \dfrac{v_t}{1 - \beta^t_2}\]更新：
\[\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t\]https://blog.csdn.net/nyist_yangguang/article/details/121603917
Adam各个参数分析
AdamW
Adam自动调整学习率，大幅提高了训练速度，但是有相当多的资料报告Adam优化的最终精度略低于SGD。问题出在哪呢，其实Adam本身没有问题，问题在于目前大多数DL框架的L2 loss实现用的是weight decay的方式，而weight decay在与Adam共同使用的时候有互相耦合。
为了解决这个问题，人们又提出了AdamW。
参考：
https://zhuanlan.zhihu.com/p/63982470
都9102年了，别再用Adam + L2 regularization了
Nadam
http://cs229.stanford.edu/proj2015/054_report.pdf
ncorporating Nesterov Momentum into Adam
AdaSecant
《ADASECANT: Robust Adaptive Secant Method for Stochastic Gradient》
Lion & Tiger
https://kexue.fm/archives/9473
Google新搜出的优化器Lion：效率与效果兼得的“训练狮”
https://kexue.fm/archives/9512
Tiger：一个“抠”到极致的优化器
cycle参数
在实际的工程实践中，某些优化策略还提供了cycle参数。它的效果如下所示：
cycle参数的初衷是为了防止训练后期LR十分小，导致结果一直在某个局部最小值附近振荡。突然调大LR可以跳出注定不会继续增长的区域探索其他区域。
上图展示了Cyclic LR的另一种用法：
每隔一段时间重启学习率，这样在单位时间内能收敛到多个局部最小值，从而得到很多个模型做集成。
二阶Optimizer
虽然二阶Optimizer的收敛效果优于一阶Optimizer，但由于计算量较大，通常用的较少。
常用的算法有BGFS和L-BFGS。
第一个拟牛顿法是由Bill Davidon、Roger Fletcher和Michael James David Powell于1959年提出的DFP算法。
到了60年代末期，作为DFP算法的改进，出现了BFGS算法。（Charles Broyden、Roger Fletcher、Donald Goldfarb、David Shanno）。
以下是部分作者的简历：
https://mp.weixin.qq.com/s/2ZfdPKo9HMjBe2QSuwWRzg
数学优化方法中的F——Roger Fletcher
https://mp.weixin.qq.com/s/dZ7TlqbgsK3RU8prJ3o-oA
宝藏数学家的优化人生（M.J.D. Powell）
参考：
http://www.cnblogs.com/kemaswill/p/3352898.html
优化算法-BFGS
http://blog.csdn.net/acdreamers/article/details/44728041
L-BFGS算法
https://mp.weixin.qq.com/s/lGrTUYALmKOQkO70DZpbPQ
小改进，大飞跃：深度学习中的最小牛顿求解器
https://mp.weixin.qq.com/s/uHrRBS3Ju9MAWbaukiGnOA
二阶梯度优化新崛起，超越Adam，Transformer只需一半迭代量
https://mp.weixin.qq.com/s/JOyHFbtO7v0DgCKVNmhyYQ
拟牛顿法：BFGS，DFP，DM条件
非梯度优化/非凸优化
对于深度学习模型的优化问题来说，随机梯度下降（SGD）是一种被广为使用方法。然而，实际上SGD并非我们唯一的选择。当我们使用一个“黑盒算法”时，即使不知道目标函数f(x):Rn→R的精确解析形式（因此不能计算梯度或Hessian矩阵）你也可以对f(x)进行评估。经典的黑盒优化方法包括“模拟退火算法”、“爬山法”以及“单纯形法”。演化策略（ES）是一类诞生于演化算法（EA）黑盒优化算法。
参考：
https://mp.weixin.qq.com/s/USHad8UvhsqWTI4MJmif5g
在深度学习模型的优化上，梯度下降并非唯一的选择
https://mp.weixin.qq.com/s/9G_7Ax9cPcQcYVqEfc-pyw
从基础知识到实际应用，一文了解“机器学习非凸优化技术”
https://zhuanlan.zhihu.com/p/27554191
非凸优化基石：Lipschitz Condition
https://mp.weixin.qq.com/s/LY1-F5hEyM40DrvobYRexA
腾讯AI Lab&北大提出基于随机路径积分的差分估计子非凸优化方法
https://mp.weixin.qq.com/s/P0qzzyVQke_c-RUF0Faitw
怎么判断一个优化问题是凸优化还是非凸优化？
https://mp.weixin.qq.com/s/NlxZQv8Z-AzIlz6mG8cCxQ
离散/整数/组合/非凸优化概述及其在AI的应用
https://www.zhihu.com/question/38677354
梯度下降法是万能的模型训练算法吗？
https://github.com/eyounx/ZOOpt
一个非梯度优化的工具
参考
http://sebastianruder.com/optimizing-gradient-descent/
An overview of gradient descent optimization algorithms
https://mp.weixin.qq.com/s/k_d02G2V4yd6HdGfw2mf1Q
从修正Adam到理解泛化：概览2017年深度学习优化算法的最新研究进展
https://mp.weixin.qq.com/s/cOCCapYrmrS_DyPkj_XRlg
常见的几种最优化方法
https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-06-speed-up-learning/
加速神经网络训练
http://www.cnblogs.com/neopenx/p/4768388.html
自适应学习率调整：AdaDelta
https://mp.weixin.qq.com/s/VoBK-l_ieSg2UupC2ix2pA
听说你了解深度学习最常用的学习算法：Adam优化算法？
您的打赏，是对我的鼓励
