ML » 机器学习(十六)——Adaboost, XGBoost, EMD
2016-12-29 :: 6201 WordsAdaboost
Adaboost是Yoav Freund和Robert Schapire于1997年提出的算法。两人后来因为该算法被授予Gödel Prize(2003)。
Yoav Freund,UCSC博士,UCSD教授。
Robert Elias Schapire,MIT博士。先后供职于Princeton University、AT&T Labs和Microsoft Research。
Gödel Prize,由欧洲计算机学会(EATCS)与美国计算机学会基础理论专业组织(ACM SIGACT)于1993年共同设立,颁给理论计算机领域最杰出的学术论文。其名称取自Kurt Gödel。
Kurt Friedrich Gödel,1906~1978,奥地利逻辑学家,数学家,哲学家,后加入美国藉。维也纳大学博士(1930)。在逻辑学方面,他是继Aristotle、Gottlob Frege之后最伟大的逻辑学家。在数学方面,他以哥德尔不完备定理著称,和Bertrand Russell、 David Hilbert、Georg Cantor齐名。
Adaboost既可用于分类问题,也可用于回归问题。这里仅针对二分类问题进行讨论。
假设我们有数据集\(\{(x_1, y_1), \ldots, (x_N, y_N)\}\),其中\(y_i \in \{-1, 1\}\),还有一系列弱分类器\(\{k_1, \ldots, k_L\}\)。
由于Boost算法是个串行算法,每次迭代就会加入一个弱分类器。这样m-1次迭代之后的分类器如下所示:
\[C_{(m-1)}(x_i) = \alpha_1k_1(x_i) + \cdots + \alpha_{m-1}k_{m-1}(x_i)\]而m次迭代之后的分类器则为:
\[C_{m}(x_i) = C_{(m-1)}(x_i) + \alpha_m k_m(x_i)\]如何选择新加入的弱分类器\(k_m\)和对应的权重\(\alpha_m\)呢?我们可以定义误差E如下所示:
\[E = \sum_{i=1}^N e^{-y_i C_m(x_i)}\]令\(w_i^{(1)} = 1,w_i^{(m)} = e^{-y_i C_{m-1}(x_i)}\),则:
\[E = \sum_{i=1}^N w_i^{(m)}e^{-y_i\alpha_m k_m(x_i)}\]因为\(k_m\)分类正确时,\(y_i k_m(x_i) = 1\),分类错误时,\(y_i k_m(x_i) = -1\)。所以:
\[E = \sum_{y_i = k_m(x_i)} w_i^{(m)}e^{-\alpha_m} + \sum_{y_i \neq k_m(x_i)} w_i^{(m)}e^{\alpha_m}\\= \sum_{i=1}^N w_i^{(m)}e^{-\alpha_m} + \sum_{y_i \neq k_m(x_i)} w_i^{(m)}(e^{\alpha_m}-e^{-\alpha_m})\]可以看出和\(k_m\)相关的实际上只有上式的右半部分。显然,使得\(\sum_{y_i \neq k_m(x_i)} w_i^{(m)}\)最小的\(k_m\),也会令E最小,这也就是我们选择加入的\(k_m\)。
对E求导,得:
\[\frac{d E}{d \alpha_m} = \frac{d (\sum_{y_i = k_m(x_i)} w_i^{(m)}e^{-\alpha_m} + \sum_{y_i \neq k_m(x_i)} w_i^{(m)}e^{\alpha_m}) }{d \alpha_m}\]令导数为0,可得:
\[\alpha_m = \frac{1}{2}\ln\left(\frac{\sum_{y_i = k_m(x_i)} w_i^{(m)}}{\sum_{y_i \neq k_m(x_i)} w_i^{(m)}}\right)\]令\(\epsilon_m = \sum_{y_i \neq k_m(x_i)} w_i^{(m)} / \sum_{i=1}^N w_i^{(m)}\),则:
\[\alpha_m = \frac{1}{2}\ln\left( \frac{1 - \epsilon_m}{\epsilon_m}\right)\]参考:
https://mp.weixin.qq.com/s/G06VDc6iTwmNGsH4IfSeJQ
Adaboost从原理到实现
https://mp.weixin.qq.com/s/PZ-1fkNvdJmv_8zLbvoW1g
Adaboost算法原理小结
https://mp.weixin.qq.com/s/KoOUgwXLOfJfOjWhbFX52Q
如果Boosting你懂,那Adaboost你懂么?
https://mp.weixin.qq.com/s/Joz2FpGgBY0tC8lpoFz8Mw
AdaBoost元算法如何提高分类性能——机器学习实战
https://mp.weixin.qq.com/s/MLEVUKse5usmKIWJF-yfOQ
通俗易懂讲解自适应提升算法AdaBoost
https://mp.weixin.qq.com/s/VuDAdeVsoZsTokh3n_wWFw
一文详解机器学习中最好用的提升方法:Boosting与AdaBoost
https://mp.weixin.qq.com/s/Jnh7yIOmzbTvWk77zh2-lA
周志华:Boosting学习理论的探索——一个跨越30年的故事
XGBoost
XGBoost是陈天奇于2014年提出的一套并行boost算法的工具库。
陈天奇,华盛顿大学计算机系博士(2019),研究方向为大规模机器学习。上海交通大学本科(2006~2010)和硕士(2010~2013)。CMU助理教授。
https://tqchen.com/
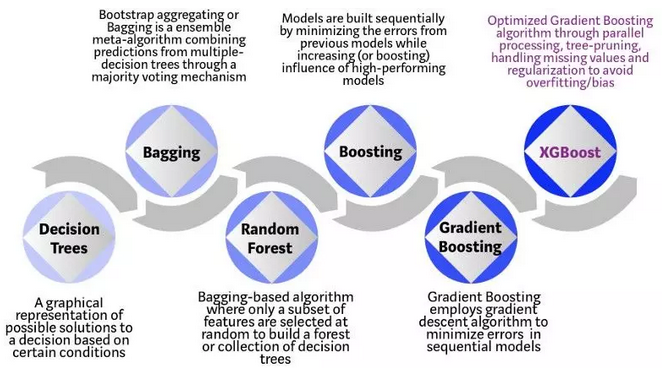
论文:
《XGBoost: A Scalable Tree Boosting System》
参考文献中的部分结论非常精彩,摘录如下。
从算法实现的角度,把握一个机器学习算法的关键点有两个,一个是loss function的理解(包括对特征X/标签Y配对的建模,以及基于X/Y配对建模的loss function的设计,前者应用于inference,后者应用于training,而前者又是后者的组成部分),另一个是对求解过程的把握。这两个点串接在一起构成了算法实现的主框架。
GBDT的求解算法,具体到每颗树来说,其实就是不断地寻找分割点(split point),将样本集进行分割,初始情况下,所有样本都处于一个结点(即根结点),随着树的分裂过程的展开,样本会分配到分裂开的子结点上。分割点的选择通过枚举训练样本集上的特征值来完成,分割点的选择依据则是减少Loss。
XGBoost的步骤:
I. 对loss function进行二阶Taylor Expansion,展开以后的形式里,当前待学习的Tree是变量,需要进行优化求解。
II. Tree的优化过程,包括两个环节:
I). 枚举每个叶结点上的特征潜在的分裂点
II). 对每个潜在的分裂点,计算如果以这个分裂点对叶结点进行分割以后,分割前和分割后的loss function的变化情况。
因为Loss Function满足累积性(对MLE取log的好处),并且每个叶结点对应的weight的求取是独立于其他叶结点的(只跟落在这个叶结点上的样本有关),所以,不同叶结点上的loss function满足单调累加性,只要保证每个叶结点上的样本累积loss function最小化,整体样本集的loss function也就最小化了。
可见,XGBoost算法之所以能够并行,其要害在于其中枚举分裂点的计算,是能够分布式并行计算的。
官网:
https://xgboost.readthedocs.io/en/latest/
GitHub:
https://github.com/dmlc/xgboost
中文文档:
http://xgboost.apachecn.org/cn/latest/
编译:
git clone --recursive https://github.com/dmlc/xgboost
cd xgboost; make -j4
python安装:
cd python-package; sudo python setup.py install
XGBoost提供了两种接口:普通接口和sklearn接口。后者的示例如下:
https://github.com/antkillerfarm/antkillerfarm_crazy/blob/master/python/ml/hello/decision_tree.py
参考
https://www.zhihu.com/question/41354392
机器学习算法中GBDT和XGBOOST的区别有哪些?
http://blog.csdn.net/sb19931201/article/details/52577592
xgboost入门与实战
https://mp.weixin.qq.com/s/x06axCC1ZTgezqEYjjNIsw
Xgboost初见面
https://mp.weixin.qq.com/s/f3QVbJiC6gLEptKwFZ-7ZQ
竞赛大杀器XGBoost,你还可以这样玩
http://blog.csdn.net/u013709270/article/details/78156207
Python机器学习实战之手撕XGBoost
https://mp.weixin.qq.com/s/xHVkc1NP2oodU7Hb0Xb_jA
为什么XGBoost在机器学习竞赛中表现如此卓越?
https://mp.weixin.qq.com/s/pn_qn6uRz2-9DmAK4sp35g
史上最详细的XGBoost实战(上)
https://mp.weixin.qq.com/s/xzZvIX0QaCPNSyGfHT3beQ
史上最详细的XGBoost实战(下)
https://mp.weixin.qq.com/s/T3NgIuGZIvmPSMNFyQeeGw
XGBoost原理解析
https://mp.weixin.qq.com/s/JYPnzgzBMSGx09ltBtfwqg
理解XGBoost机器学习模型的决策过程
http://www.cnblogs.com/qcloud1001/p/7542128.html
小巧玲珑:机器学习届快刀XGBoost的介绍和使用
https://mp.weixin.qq.com/s/__ESveAdBS9KJf26R3EMVA
对比TensorFlow提升树与XGBoost:我们该使用怎样的梯度提升方法
https://mp.weixin.qq.com/s/_uscpKaRXZbwfMiWGoY0Uw
多GPU加速学习,这是一份崭新的XGBoost库
https://mp.weixin.qq.com/s/pwuOFj_rT5Z_XY9siZosKQ
线性模型已退场,XGBoost时代早已来
https://mp.weixin.qq.com/s/hYuBHHfAGLO3Y0l5t6y94Q
XGBoost缺失值引发的问题及其深度分析
https://mp.weixin.qq.com/s/Il_S6y4UkN5nim91mwVcVw
缺失值处理
https://mp.weixin.qq.com/s/wgiNutl3FhJSAtfJNd5B5g
Xgboost
https://mp.weixin.qq.com/s/jZ3vcCcZTfTmJNl-9QXelw
XGBoost超详细推导,终于有人讲明白了!
https://mp.weixin.qq.com/s/HcWoDmrp4taRGREvV7x4vA
斯坦福吴恩达团队提出NGBoost:用于概率预测的自然梯度提升
https://mp.weixin.qq.com/s/X4K6UFZPxL05v2uolId7Lw
XGBoost在携程搜索排序中的应用
https://mp.weixin.qq.com/s/5zSLod4oyL4m6LADI6KC0Q
深入理解XGBoost,优缺点分析,原理推导及工程实现
https://mp.weixin.qq.com/s/uvUN4JiqSb-bS4HAVCDTIQ
集成模型Xgboost!机器学习最热研究方向入门,附学习路线图
https://mp.weixin.qq.com/s/-aRRORqBnTMmBDXuW749_w
在没有技术术语的情况下介绍Adaptive、GBDT、XGboosting等提升算法的原理简介
https://mp.weixin.qq.com/s/umGzRySCnJo25e5_0nO7cw
如何用XGBoost做时间序列预测?
https://mp.weixin.qq.com/s/QYMPBWMVTQf3LACGGWGX7A
样本不平衡处理:xgboost几种权重设置方法比较
https://mp.weixin.qq.com/s/d6sVDAKnaU97mAeDs_Gedg
从零解读Xgboost(原理+代码)
https://mp.weixin.qq.com/s/YunDfYPLywc0tMJF72YIAQ
数据分析利器:XGBoost算法最佳解析
https://mp.weixin.qq.com/s/QAu0nM72E2gVhbRXmtCMcw
XGBoost和时间序列
https://www.zhihu.com/question/359567100
XGBoost为什么若模型决策树的叶子节点值越大,越容易过拟合呢?
EMD
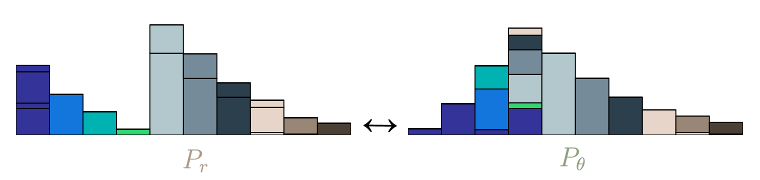
推土机距离(Earth mover’s distance)是两个概率分布之间的距离度量的一种方式。如果将区间D的概率分布比作沙堆P,那么\(P_r\)和\(P_\theta\)之间的EMD距离,就是推土机将\(P_r\)改造为\(P_\theta\)所需要的工作量。
EMD的计算公式为:
\[EMD(P_r,P_\theta) = \frac{\sum_{i=1}^m \sum_{j=1}^n f_{i,j}d_{i,j}}{\sum_{i=1}^m \sum_{j=1}^n f_{i,j}}\]其中,f表示土方量,d表示运输距离。
然而,搬运土方的方案并不唯一,有的聪明,有的愚笨。因此,两个分布的EMD距离,通常指的是,所有方案的EMD距离的最小值。
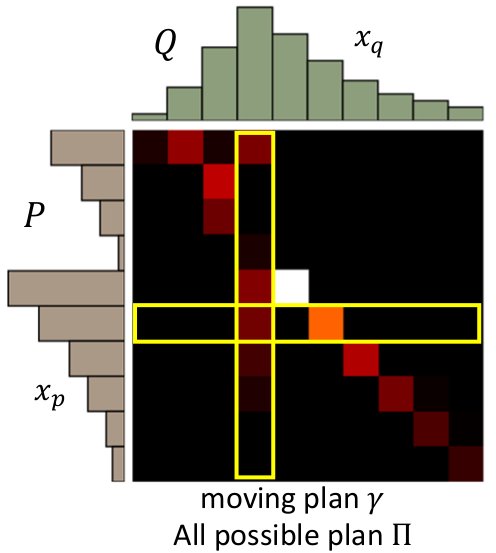
一般来说,可用上面这样的矩阵来可视化并计算EMD距离。
这个问题实际是线性规划中的运输问题,可以用匈牙利算法迭代求解。最终求得的最小值就是EMD。
最优方案也被称为“最优传输”,相关的研究被称作“最优传输理论”。法国数学家蒙日最早研究过该类问题。

您的打赏,是对我的鼓励
