ML » 机器学习（十五）——决策树
2016-10-13 :: 5754 Words协同过滤的ALS算法（续）
https://zhuanlan.zhihu.com/p/130314852
一文读懂协同推荐算法原理（上）
https://zhuanlan.zhihu.com/p/132396111
一文读懂协同推荐算法原理（下）
https://mp.weixin.qq.com/s/z13iXMwJNzHfMCeXxYGRug
一文带你了解协同过滤的前世今生
https://mp.weixin.qq.com/s/ianqpVVsks9NlMGYesWPIQ
从原理到实践，万字长文解析矩阵分解推荐算法
决策树
Decision Tree讲的最好的，首推周志华的《机器学习》。这里只对要点进行备忘。
当前样本集合D中，第k类样本所占的比例为\(p_k(k=1,2,\dots,\mid y\mid)\)，则D的信息熵（information entropy）定义为：
\[Ent(D)=-\sum_{k=1}^{\mid y\mid }p_k\log_2p_k\]假定离散属性a有V个可能的取值，若使用a对D进行划分，则第v个分支结点包含了D中所有在a上取值\(a^v\)的样本，记为\(D^v\)。则信息增益（information gain）为：
\[Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{\mid D^v\mid }{\mid D\mid }Ent(D^v)\]增益率（gain ratio）：
\[Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\]其中
\[IV(a)=-\sum_{v=1}^V\frac{\mid D^v\mid }{\mid D\mid }\log_2 \frac{\mid D^v\mid }{\mid D\mid }\]基尼值：
\[Gini(D)=1-\sum_{k=1}^{\mid y\mid }p_k^2\]基尼指数：
\[Gini\_index(D,a)=\sum_{v=1}^V\frac{\mid D^v\mid }{\mid D\mid }Gini(D^v)\]各种决策树和它的划分依据如下表所示：
| 名称 | 划分依据 |
|---|---|
| ID3 | Gain |
| C4.5 | Gain_ratio |
| CART | Gini_index |
决策树是一种可以将训练误差变为0的算法，只要每个样本对应一个叶子结点即可，然而这样做会导致过拟合。为了限制树的生长，我们可以加入阈值，当增益大于阈值时才让节点分裂。
参考：
https://mp.weixin.qq.com/s/TTU9LMG8TuB1gzgfCfWjjw
从香农熵到手推KL散度：一文带你纵览机器学习中的信息论
https://mp.weixin.qq.com/s/HZUDg8-39pF4E4wB1ZemOw
小孩都看得懂的基尼不纯度
Lorenz curve
既然提到了基尼值，那么就再谈一下Lorenz curve吧。
Max Otto Lorenz，1876～1959，美国经济学家。University of Wisconsin–Madison博士（1906）。美国统计学会会员。
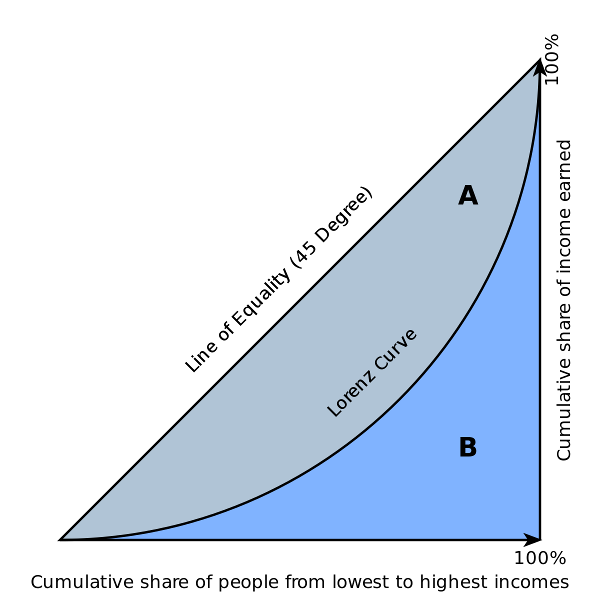
上图就是Lorenz curve。它的横轴是人数（按照财富值从低到高排列），纵轴是财富数量。显然，从坐标原点到正方形相应另一个顶点的对角线为均等线，即收入分配绝对平等线，这一般是不存在的。实际收入分配曲线，即洛伦兹曲线都在均等线的右下方。
Corrado Gini，1884～1965，意大利统计学家。意大利统计学会主席。政治方面支持法西斯统治，但反对排犹。
Lorenz curve将右下方分为了A和B两部分，Gini据此提出了Gini coefficient：\(G=A/(A+B）\)。
显然，如果采用等（横轴）间距采样的话，Gini coefficient就等于上节提到的Gini(D)了。
GBDT
GBDT这个算法有很多名字，但都是同一个算法：
GBRT(Gradient Boost Regression Tree)渐进梯度回归树
GBDT(Gradient Boost Decision Tree)渐进梯度决策树
MART(Multiple Additive Regression Tree)多决策回归树
Tree Net决策树网络
GBDT属于集成学习（Ensemble Learning）的范畴。集成学习的思路是在对新的实例进行分类的时候，把若干个单个分类器集成起来，通过对多个分类器的分类结果进行某种组合来决定最终的分类，以取得比单个分类器更好的性能。
集成学习的算法主要分为两大类：
并行算法：若干个不同的分类器同时分类，选择票数多的分类结果。这类算法包括bagging和随机森林等。
串行算法：使用同种或不同的分类器，不断迭代。每次迭代的目标是缩小残差或者提高预测错误项的权重。这类算法包括Adaboost和GBDT等各种Boosting算法。
这些Boosting算法的差异在于：
1）如何计算学习误差率e?
2) 如何得到弱学习器权重系数\(\alpha\)?
3）如何更新样本权重D?
4) 使用何种结合策略？
只要是Boosting家族的算法，都要解决这4个问题。
GBDT写的比较好的，有以下blog：
http://blog.csdn.net/w28971023/article/details/8240756
GBDT（MART）迭代决策树入门教程
摘录要点如下：
决策树分为两大类：
回归树：用于预测实数值，如明天的温度、用户的年龄、网页的相关程度。其结果加减是有意义的，如10岁+5岁-3岁=12岁。
分类树：用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。其结果加减无意义，如男+男+女=到底是男是女？
GBDT的核心在于累加所有树的结果作为最终结果。例如根到某叶子结点的路径上的决策值为10岁、5岁、-3岁，则该叶子的最终结果为10岁+5岁-3岁=12岁。
所以GBDT中的树都是回归树，不是分类树。
上面举的例子中，越靠近叶子，其决策值的绝对值越小。这不是偶然的。决策树的基本思路就是“分而治之”，自然越靠近根结点，其划分的粒度越粗。每划分一次，预测误差（即残差r）就小一点。
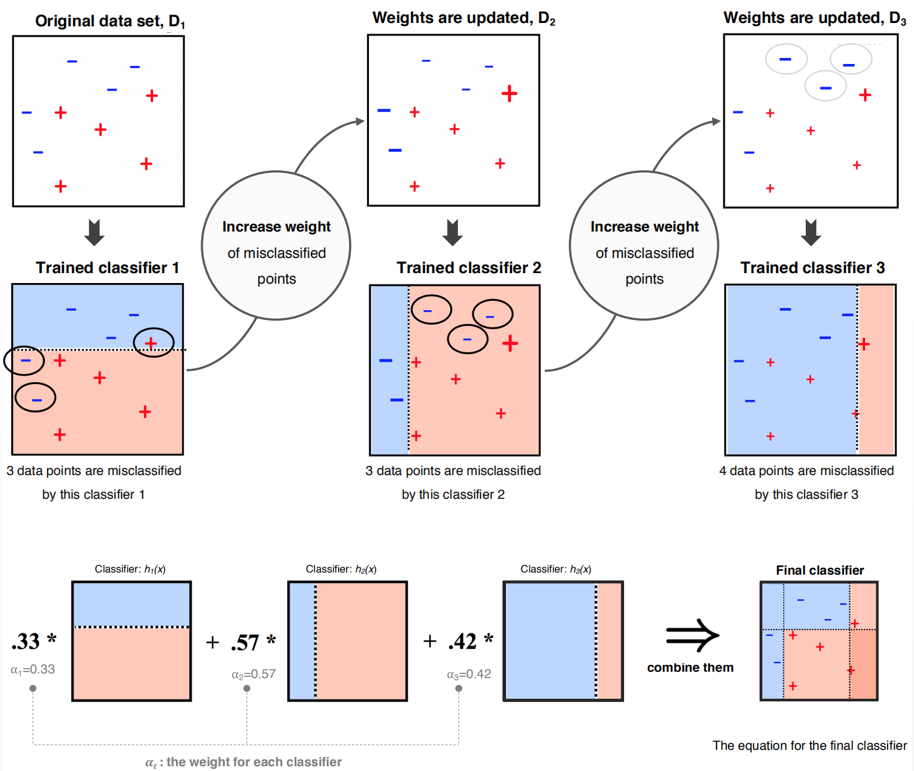
我们将\(\{x^{(i)},r^{(i)}\}\)组成训练集，交给下一步的弱分类器，这样也就变相提高了下一步划分中预测错误项的权重。由于这个过程，在原理上和梯度下降类似，这也就是算法名称中Gradient的由来，尽管实际上我们并不需要求导计算Gradient。
为了防止过拟合，GBDT还采用了Shrinkage（缩减）的思想，每次只走一小步来逐渐逼近结果，这样各个树的残差就是渐变的，而不是陡变的。
参考：
http://blog.csdn.net/u010691898/article/details/38292937
阿里大数据比赛总结
Bagging和随机森林
Bagging主要是通过随机选择样本集，来改变各并行计算决策树的结果，从而达到并行计算的效果。这相当于通过加入样本的扰动，来提供泛化能力。
随机森林除了样本扰动之外，还通过随机选择属性集，并从中选择一个最优属性划分的方式，进一步提升了模型的泛化能力。
参考
https://mp.weixin.qq.com/s/XnMXXFEBPXnEUk3jdMMoXA
从决策树到随机森林：树型算法的原理与实现
https://mp.weixin.qq.com/s/NcBGYtgiWa0uY48wnFOoVg
机器学习之决策树算法
https://mp.weixin.qq.com/s/DTDH2m21Gz1UQ2tW64kPZg
如何解读决策树和随机森林的内部工作机制？
https://mp.weixin.qq.com/s/LC41Mk7Sjm30qr1KXsZd8Q
机器学习利器——决策树和随机森林！
https://mp.weixin.qq.com/s/3yVosp2Kgp8cUyYWw_ULvw
如何解读决策树和随机森林的内部工作机制？
https://mp.weixin.qq.com/s/hY5cEug3xEpkkPE1X0Ykvg
GBDT详解
https://mp.weixin.qq.com/s/JU0H1cYIyWLgOkdBgra-eA
GBDT！深入浅出详解梯度提升决策树
https://mp.weixin.qq.com/s/0CSAh9LtYj1wwCipCMGo9g
深入理解GBDT回归算法
https://mp.weixin.qq.com/s/KyvjI_2CLss_fzVFxPrE7A
Facebook经典模型LR+GBDT理论与实践
https://mp.weixin.qq.com/s/-AwJvJ_YQ7p_yo5TNHTOfw
决策树的python实现
https://mp.weixin.qq.com/s/PkUPGnsfCjiGPJpOmjACkA
Bagging与随机森林
https://mp.weixin.qq.com/s/XbrnhlxUbmK0JzQ4I_X2wQ
决策树之随机森林
https://mp.weixin.qq.com/s/NY2E2c808WSacyj68TFInw
决策树模型组合理解
https://mp.weixin.qq.com/s/K2uh0J-BLj-eSriI1_mEjA
决策树分类和预测算法原理
https://mp.weixin.qq.com/s/I5AXiHrN02zpyhF85Ze-jg
从零开始学习Gradient Boosting算法
https://mp.weixin.qq.com/s/6X27b97X_7OOOSijqAau9g
随机森林（Random Forest）
https://zhuanlan.zhihu.com/p/179286622
Random Forest可以用来做聚类吗？
https://mp.weixin.qq.com/s/2EtQTsumOcHmYFjxOlPApQ
决策树算法及实现
https://mp.weixin.qq.com/s/epHGb0dq9mX6O4PGw3x8aA
机器学习基础算法之随机森林
https://mp.weixin.qq.com/s/EXOqekYaKpGHGSFOH_gxfA
“神经网络”能否代替“决策树算法”？
https://mp.weixin.qq.com/s/NoeGzkZJVbbYG-mP_HZ4qQ
一文详解决策树算法模型
https://mp.weixin.qq.com/s/NTgzCXvbdXDR4N5J5z9Xpw
通俗解释随机森林算法
https://mp.weixin.qq.com/s/F9jzF50910ZGupSZNNnHtQ
机器学习实战之决策树
https://mp.weixin.qq.com/s/rV4R-y2VYE8RJlClvQV5zQ
决策树的理论与实践
https://mp.weixin.qq.com/s/mhD1U_iJm7NNXCTRLLifkw
Bagging与随机森林算法原理小结
https://mp.weixin.qq.com/s/gKQw8saCgSW6JkyocHvKqg
关于决策树的那些事
https://mp.weixin.qq.com/s/nwd4zXy6hTjt6Hx9e7QMFg
常用的模型集成方法介绍：bagging、boosting、stacking
https://mp.weixin.qq.com/s/f8kVIBlqZxS_U8FdMTRGVw
决策树算法原理（上）
https://mp.weixin.qq.com/s/ku942npFMgXxOrm0Xam-Cg
决策树算法原理（下）
https://blog.csdn.net/CoderPai/article/details/90900707
bagging方法
https://blog.csdn.net/CoderPai/article/details/92018343
随机森林的实现与解释
https://mp.weixin.qq.com/s/jj3BtmnWRAwCS56ZU3ZXZA
最常见核心的决策树算法—ID3、C4.5、CART
https://mp.weixin.qq.com/s/vkbZweJ5oRo4IPt-3kg64g
决策树算法十问及经典面试问题
https://mp.weixin.qq.com/s/t2B5dg8uELNqSJcENHiwNA
深入理解GBDT多分类算法
https://mp.weixin.qq.com/s/Cdi0CcWDLgS6Kk7Kx71Vaw
深入理解提升树（Boosting Tree）算法
https://mp.weixin.qq.com/s/fsT6rzpL5cuzh2usNjzzbA
一文学习模型融合！从加权融合到stacking, boosting
https://mp.weixin.qq.com/s/lTAekav7kgcbF47Yk-LL-g
最全！两万字带你完整掌握八大决策树！
https://mp.weixin.qq.com/s/pJe3-XiMwaIQmSzwSgTqhA
硬核拆解GBDT，带你入门机器学习
https://mp.weixin.qq.com/s/e80sWpiXykKHnq6RaLGEyQ
GBDT与LR的区别总结
https://www.cnblogs.com/always-fight/p/9400346.html
GBDT用于分类问题
https://mp.weixin.qq.com/s/mHZBDY_uFfwVBvHgFXQuqw
决策树是如何选择特征和分裂点？
您的打赏，是对我的鼓励
