ML » 机器学习(六)——SVM(2)
2016-08-23 :: 7026 WordsSVM
核函数(续)
讨论另一个核函数:
\[K(x,z)=\exp\left(-\frac{\|x-z\|^2}{2\sigma^2}\right)\]这个核函数被称为高斯核函数(Gaussian kernel),对应的\(\phi(x)\)是个无限维的向量。
\((a+b)^n\)是个p为0.5的二项分布,由棣莫佛-拉普拉斯定理(de Moivre–Laplace theorem)可知,当\(n\to\infty\)时,它的极限是正态分布。
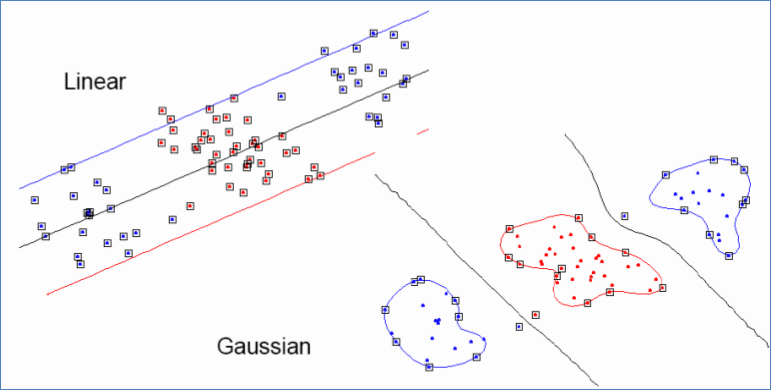
Gaussian kernel也叫做Radial Basis Function(RBF) kernel,即径向基函数。
参考:
https://mp.weixin.qq.com/s/e-dGnE4Egepmp1OOaOJoNQ
例子通俗解释机器学习中核函数的定义和作用
https://mp.weixin.qq.com/s/VF7yWMYyPGbLmVMmV_G-bQ
通俗易懂讲解RBF网络
核函数的有效性
如果对于给定的核函数K,存在一个特征映射\(\phi\),使得\(K(x,z)=\phi(x)^T\phi(z)\),则称K为有效核函数。
我们首先假设K为有效核函数,来看看它有什么性质。假设有m个样本\(\{x^{(1)},\dots,x^{(m)}\}\),我们定义\(m\times m\)维的矩阵k:\(K_{ij}=K(x_i,x_j)\)。这个矩阵被称为核矩阵(Kernel matrix)。
\[K_{ij}=K(x_i,x_j)=\phi(x^{(i)})^T\phi(x^{(j)})=\phi(x^{(j)})^T\phi(x^{(i)})=K(x_j,x_i)=K_{ji}\]如果我们用\(\phi_k(x)\)表示\(\phi(x)\)第k个元素的话,则对于任意向量z:
\[\begin{align}z^TKz&=\sum_i\sum_jz_iK_{ij}z_j=\sum_i\sum_jz_i\phi(x^{(i)})^T\phi(x^{(j)})z_j \\&=\sum_i\sum_jz_i\sum_k\phi_k(x^{(i)})\phi_k(x^{(j)})z_j=\sum_k\sum_i\sum_jz_i\phi_k(x^{(i)})\phi_k(x^{(j)})z_j \\&=\sum_k\left(\sum_iz_i\phi_k(x^{(i)})\right)^2\ge 0 \end{align}\]即K矩阵是半正定矩阵。事实上,K矩阵是对称半正定矩阵,不仅是K函数有效的必要条件,也是它的充分条件。相关的证明是由James Mercer给出的,被称为Mercer定理(Mercer Theorem)。
James Mercer,1883-1932,英国数学家,英国皇家学会会员,毕业于剑桥大学。曾服役于英国皇家海军,参加了日德兰海战。
Mercer定理给出了不用找到\(\phi(x)\),而判定\(K(x,z)\)是否有效的方法。因此寻找\(\phi(x)\)的步骤就可以跳过了,直接使用\(K(x,z)\)替换上面公式中的\(\langle x,z\rangle\)即可。例如:
\[w^Tx+b=\sum_{i\in SV}\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b=\sum_{i\in SV}\alpha_iy^{(i)}K(x^{(i)},x)+b \tag{6}\]核函数不仅仅用在SVM上,但凡在一个算法中出现了\(\langle x,z\rangle\),我们都可以使用\(K(x,z)\)去替换,这可以很好地改善我们算法的效率。因此,核函数更多的被看作是一种技巧而非理论(kernel trick)。
构造新核的技术
给定有效的核\(k_1(x,x')\)和\(k_2(x, x')\),下面的新核也是有效的:
\[\begin{eqnarray} k(x,x') &=& k_1(x,x') \\ k(x,x') &=& f(x)k_1(x,x')f(x') \\ k(x,x') &=& q(k_1(x,x')) \\ k(x,x') &=& \exp(k_1(x,x')) \\ k(x,x') &=& k_1(x,x') + k_2(x,x') \\ k(x,x') &=& k_1(x,x')k_2(x,x') \\ k(x,x') &=& k_3(\phi{x},\phi{x'}) \\ k(x,x') &=& x^TAx' \\ k(x,x') &=& k_a(x_a,x_a') + k_b(x_b,x_b') \\ k(x,x') &=& k_a(x_a,x_a')k_b(x_b,x_b') \end{eqnarray}\]其中\(c>0\)是一个常数,\(f(\cdot)\)是任意函数,\(q(\cdot)\)是一个系数非负的多项式,\(\phi(x)\)是一个从\(x\)到\(\mathbb{R}^M\)的函数,\(k_3(\cdot, \cdot)\)是\(\mathbb{R}^M\)中的一个有效的核,\(A\)是一个对称半正定矩阵,\(x_a, x_b\)是变量(未必不相交),且\(x = (x_a, x_b)\)。\(k_a,k_b\)是各自空间的有效的核函数。
核函数的局限性
目前来说,核函数的选择仍然是个未决问题,通常的做法是同时使用不同的核来计算,选择其中较优的结果,这实际上是集成学习的范畴了。
规则化和不可分情况处理
我们之前讨论的情况都是建立在样例线性可分的假设上,当样例线性不可分时,我们可以尝试使用核函数来将特征映射到高维,这样很可能就可分了。然而,映射后我们也不能100%保证可分。那怎么办呢,我们需要将模型进行调整,以保证在不可分的情况下,也能够尽可能地找出分隔超平面。
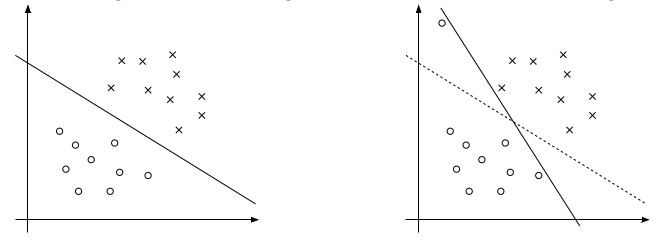
上面的右图中可以看到一个离群点(可能是噪声),它会造成超平面的移动,从而导致边距缩小,可见以前的模型对噪声非常敏感。再有甚者,如果离群点在另外一个类中,那么这时候就是线性不可分的了。
这时候应该允许一些点游离并在模型中违背限制条件(函数间隔大于1)。我们设计得到新的模型如下(也称软间隔(Soft-margin)):
\[\begin{align} &\operatorname{min}_{\gamma,w,b}& & \frac{1}{2}\|w\|^2+C\sum_{i=1}^m\xi_i\\ &\operatorname{s.t.}& & y^{(i)}(w^Tx^{(i)}+b)\ge 1-\xi_i,i=1,\dots,m\\ & & & \xi_i\ge 0,i=1,\dots,m \end{align}\]这里的C是离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。我们看到,目标函数控制了离群点的数目和程度,使大部分样本点仍然遵守限制条件。
模型修改后,拉格朗日公式修改如下:
\[\mathcal{L}(w,b,\xi,\alpha,r)=\frac{1}{2}w^Tw+C\sum_{i=1}^m\xi_i-\sum_{i=1}^m\alpha_i[y^{(i)}(w^Tx^{(i)}+b)-1+\xi_i]-\sum_{i=1}^mr_i\xi_i\]其对偶优化问题为:
\[\begin{align} &\operatorname{max}_\alpha & & W(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle\\ &\operatorname{s.t.}& & 0\le\alpha_i\le C,i=1,\dots,m\\ & & & \sum_{i=1}^m\alpha_iy^{(i)}=0 \end{align}\]此时,我们发现没有了参数\(\xi_i\),与之前模型唯一不同在于\(\alpha_i\)多了\(\alpha_i\le C\)的限制条件。需要注意的是,b的求值公式发生了改变,这将在SMO算法里面介绍。
坐标上升法
\[\begin{align} &\operatorname{max}_\alpha & & W(\alpha_1,\dots,\alpha_m) \end{align}\]对于上面这个优化问题,除了之前介绍的梯度下降法和牛顿法之外,还有坐标上升法(Coordinate ascent)。其过程为:
Loop until convergence:{
for i=1 to m, {
\[\alpha_i:=\arg\max_{\hat\alpha_i}W(\alpha_1,\dots,\alpha_{i-1},\hat\alpha_i,\alpha_{i+1},\dots,\alpha_m)\]}
}
最里面语句的意思是固定除\(\alpha_i\)之外的所有\(\alpha_j(j\neq i)\),这时W可看作只是关于\(\alpha_i\)的函数,那么直接对\(\alpha_i\)求导优化即可。这里我们进行最大化求导的顺序是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
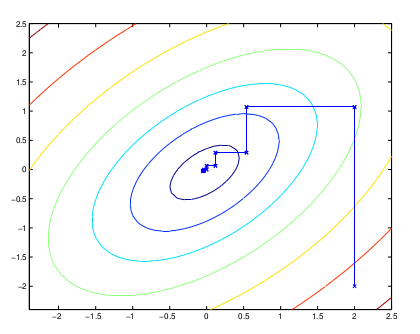
图中的直线表示迭代优化的路径,可以看到每一步前进路线都是平行于坐标轴的,因为每一步只优化一个变量。
序列最小优化方法
序列最小优化方法(Sequential Minimal Optimization,SMO)算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对SVM和数据稀疏时性能更优。关于SMO最好的资料就是他本人写的《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》。
John Carlton Platt,1963年生,14岁进入加州州立大学长滩分校,加州理工学院博士。先后供职于Synaptics和Microsoft Research,现为Google首席科学家。
针对之前列出的SVM对偶优化问题:
\[\begin{align} &\operatorname{max}_\alpha & & W(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle \tag{1}\\ &\operatorname{s.t.}& & 0\le\alpha_i\le C,i=1,\dots,m \tag{2}\\ & & & \sum_{i=1}^m\alpha_iy^{(i)}=0 \tag{3} \end{align}\]我们可以考虑使用坐标上升法,即首先固定除\(\alpha_1\)以外的所有参数,然后在\(\alpha_1\)上求极值。然而由于约束3的存在,把除\(\alpha_1\)以外的所有参数固定,实际上也就把\(\alpha_1\)给固定了。因此,需要一定的技巧来处理,比如:
Repeat till convergence:{
1.挑选一对\(\alpha_i\)和\(\alpha_j\)(挑选的规则可以是启发式的,以收敛快为准则)
2.固定除\(\alpha_i\)和\(\alpha_j\)之外的其余参数,以确定W极值条件下的\(\alpha_i\)和\(\alpha_j\)}
这里假设我们固定\(\alpha_3,\dots,\alpha_m\),来优化\(\alpha_1\)和\(\alpha_2\)。由约束3可得:
\[\alpha_1y^{(1)}+\alpha_2y^{(2)}=-\sum_{i=3}^m\alpha_iy^{(i)}=\zeta\tag{4}\]因为\(\alpha_3,\dots,\alpha_m\)的值已经固定,所以\(\zeta\)实际上是个常数。
同理:
\[\begin{align} W(\alpha)&=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_jK_{ij} \\&\begin{split} =\alpha_1+\alpha_2+\sum_{i=3}^m\alpha_i-\frac{1}{2}\left(\sum_{i,j=1}^2y^{(i)}y^{(j)}\alpha_i\alpha_jK_{ij}+2\sum_{j=3}^my^{(1)}y^{(j)}\alpha_1\alpha_jK_{1j} \\+2\sum_{j=3}^my^{(2)}y^{(j)}\alpha_2\alpha_jK_{2j}+\sum_{i,j=3}^my^{(i)}y^{(j)}\alpha_i\alpha_jK_{ij}\right) \end{split} \\&=\alpha_1+\alpha_2+\psi_1-\frac{1}{2}\sum_{i,j=1}^2y^{(i)}y^{(j)}\alpha_i\alpha_jK_{ij}-\sum_{j=3}^my^{(1)}y^{(j)}\alpha_1\alpha_jK_{1j}-\sum_{j=3}^my^{(2)}y^{(j)}\alpha_2\alpha_jK_{2j}-\psi_2 \\&=\alpha_1+\alpha_2-\frac{1}{2}\left((y^{(1)})^2\alpha_1^2K_{11}+(y^{(2)})^2\alpha_2^2K_{22}+2y^{(1)}y^{(2)}\alpha_1\alpha_2K_{12}\right) \\&\qquad-y^{(1)}\alpha_1\sum_{j=3}^my^{(j)}\alpha_jK_{1j}-y^{(2)}\alpha_2\sum_{j=3}^my^{(j)}\alpha_jK_{2j}+\psi_3 \\&=\alpha_1+\alpha_2-\frac{1}{2}\alpha_1^2K_{11}-\frac{1}{2}\alpha_2^2K_{22}-s\alpha_1\alpha_2K_{12}-y^{(1)}\alpha_1v_1-y^{(2)}\alpha_2v_2+\psi_3 \tag{5} \end{align}\]其中,\(\psi_i\)表示常数项,\(s=y^{(1)}y^{(2)}\),\(v_i=\sum_{j=3}^my^{(j)}\alpha_jK_{ij}\)。
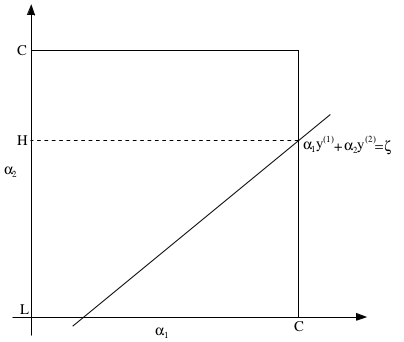
如上图所示,因为约束2的存在,\(\alpha_1\)和\(\alpha_2\)的值实际上被固定在如图所示的\([0,C]\times[0,C]\)的方框内。根据约束3可得,\(\alpha_1\)和\(\alpha_2\)落在图中的直线上。从图中还可看出\(L\le \alpha_2\le H\),其严格定义如下:
\[\begin{align} L=\max(0,\alpha_2-\alpha_1),H=\min(C,C+\alpha_2-\alpha_1) & & if\ y^{(1)}\neq y^{(2)}\\ L=\max(0,\alpha_2+\alpha_1-C),H=\min(C,\alpha_2+\alpha_1) & & if\ y^{(1)}= y^{(2)} \end{align}\]
您的打赏,是对我的鼓励
