• SVM
  • 拉格朗日对偶（续）
  • KKT条件
  • 支持向量
  • 核函数

SVM

拉格朗日对偶（续）

上述约束优化问题也被称为原始优化问题（primal optimization problem）。为了求解这个问题，我们定义广义拉格朗日（generalized Lagrangian）函数：

\[\mathcal{L}(w,\alpha,\beta)=f(w)+\sum_{i=1}^k\alpha_ig_i(w)+\sum_{i=1}^l\beta_ih_i(w)\]

利用这个函数可以将约束优化问题转化为无约束优化问题。其中的\(\alpha_i\)、\(\beta_i\)也被称作拉格朗日乘子（Lagrange multiplier）。

\[\theta_\mathcal{P}(w)=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\mathcal{L}(w,\alpha,\beta)=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}f(w)+\sum_{i=1}^k\alpha_ig_i(w)+\sum_{i=1}^l\beta_ih_i(w)\]

其中，\(\mathcal{P}\)代表原始优化问题，\(\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\)表示在\(\alpha,\beta\)变化，而其他变量不变的情况下，求最大值。

如果w不满足约束，也就是\(g_i(w)>0\)或\(h_i(w)\ne 0\)。这时由于\(\mathcal{L}\)函数是无约束函数，\(\alpha_i\)、\(\beta_i\)可以任意取值，因此\(\sum_{i=1}^k\alpha_ig_i(w)\)或\(\sum_{i=1}^l\beta_ih_i(w)\)并没有极值，也就是说\(\theta_\mathcal{P}(w)=\infty\)。

反之,如果w满足约束，则\(\sum_{i=1}^k\alpha_ig_i(w)\)和\(\sum_{i=1}^l\beta_ih_i(w)\)都为0，因此\(\theta_\mathcal{P}(w)=f(w)\)。

综上：

\[\theta_\mathcal{P}(w)=\begin{cases} f(w), & w满足约束 \\ \infty, & w不满足约束 \\ \end{cases}\]

我们定义：

\[p^*=\underset{w}{\operatorname{min}}\theta_\mathcal{P}(w)=\underset{w}{\operatorname{min}}\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\mathcal{L}(w,\alpha,\beta)\]

下面我们定义对偶函数：

\[\theta_\mathcal{D}(w)=\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)\]

这里的\(\mathcal{D}\)代表原始优化问题的对偶优化问题。仿照原始优化问题定义如下：

\[d^*=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\theta_\mathcal{D}(w)=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)\]

这里我们不加证明的给出如下公式：

\[d^*=\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\underset{w}{\operatorname{min}}\mathcal{L}(w,\alpha,\beta)\le\underset{w}{\operatorname{min}}\underset{\alpha,\beta:\alpha_i\ge 0}{\operatorname{max}}\mathcal{L}(w,\alpha,\beta)=p^*\]

这样的对偶问题被称作拉格朗日对偶（Lagrange duality）。

参考：

https://mp.weixin.qq.com/s/IhvdhEnyRI2DRns9EkCy5Q

拉格朗日对偶理论

https://www.zhihu.com/question/58584814

如何通俗地讲解对偶问题？尤其是拉格朗日对偶lagrangian duality？

KKT条件

拉格朗日对偶公式中使\(p^*=d^*\)成立的条件，被称为KKT条件（Karush-Kuhn-Tucker conditions）：

\[\begin{align} \frac{\partial}{\partial w_i}\mathcal{L}(w^*,\alpha^*,\beta^*) & =0,i=1,\dots,n & \\ \frac{\partial}{\partial \beta_i}\mathcal{L}(w^*,\alpha^*,\beta^*) & =0,i=1,\dots,l & \\ \alpha_i^*g_i(w^*)& =0,i=1,\dots,k & \tag{1}\\ g_i(w^*)& \le 0,i=1,\dots,k & \\ \alpha_i^* & \ge 0,i=1,\dots,k & \\ \end{align}\]

其中的\(w^*,\alpha^*,\beta^*\)表示满足KKT条件的相应变量的取值。条件1也被称为KKT对偶互补条件（KKT dual complementarity condition）。显然这些\(w^*,\alpha^*,\beta^*\)既是原始问题的解，也是对偶问题的解。

严格的说，KKT条件是非线性约束优化问题存在最优解的必要条件。这个问题的充分条件比较复杂，这里不做讨论。

Harold William Kuhn，1925～2014，美国数学家，普林斯顿大学教授。

Albert William Tucker，1905～1995，加拿大数学家，普林斯顿大学教授。

William Karush，1917～1997，美国数学家，加州州立大学北岭分校教授。（注意，California State University和University of California是不同的学校）

参考：

https://mp.weixin.qq.com/s/AKTGyHlbCj0P949K-LAv6A

拉格朗日乘数法

https://www.zhihu.com/question/64834116

拉格朗日乘子法漏解的情况？

https://mp.weixin.qq.com/s/UyNpJZ7k_q1qVdcNhrzDcQ

直观详解：拉格朗日乘法和KKT条件

https://mp.weixin.qq.com/s/PELnlB5vMV0gGJbL6BzoIA

原始-对偶算法的设计原理

https://mp.weixin.qq.com/s/5655NgkxrbK3qtA4Ilxd4w

为何引入对偶问题

https://mp.weixin.qq.com/s/PRKEIW3HEafytUNscHSLpA

如何写对偶问题

支持向量

针对最优边距分类问题，我们定义：

\[g_i(w)=-y^{(i)}(w^Tx^{(i)}+b)+1\le 0\]

由KKT对偶互补条件可知，如果\(\alpha_i>0\)，则\(g_i(w)=0\)。

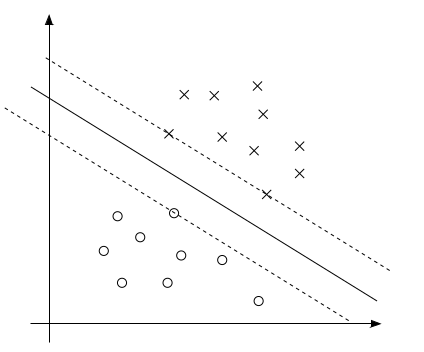
上图中的实线表示最大边距的分割超平面。由之前对于边距的几何意义的讨论可知，只有离该分界线最近的几个点（即图中的所示的两个x点和一个o点）才会取得约束条件的极值，即\(g_i(w)=0\)。也只有这几个点的\(\alpha_i>0\)，其余点的\(\alpha_i=0\)。这样的点被称作支持向量（support vectors）。显然支持向量的数量是远远小于样本集的数量的。

为我们的问题构建拉格朗日函数如下：

\[\mathcal{L}(w,b,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^m\alpha_i[y^{(i)}(w^Tx^{(i)}+b)-1] \tag{2}\]

为了求解

\[\theta_\mathcal{D}(\alpha)=\underset{w,b}{\operatorname{min}}\mathcal{L}(w,b,\alpha)\]

可得：

\[\nabla_w\mathcal{L}(w,b,\alpha)=w-\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}=0\]

即

\[w=\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)} \tag{3}\]

对b求导可得：

\[\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha)=\sum_{i=1}^m\alpha_iy^{(i)}=0 \tag{4}\]

把公式3代入公式2，可得：

\[\begin{align}\mathcal{L}(w,b,\alpha)&=\frac{1}{2}\|w\|^2-\sum_{i=1}^m\alpha_i[y^{(i)}(w^Tx^{(i)}+b)-1] \\&=\frac{1}{2}w^Tw-\sum_{i=1}^m\alpha_iy^{(i)}w^Tx^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}w^Tx^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-\sum_{i=1}^m\alpha_iy^{(i)}b+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}w^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}\left(\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}\right)^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=-\frac{1}{2}\sum_{i=1}^m\alpha_iy^{(i)}(x^{(i)})^T\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}-b\sum_{i=1}^m\alpha_iy^{(i)}+\sum_{i=1}^m\alpha_i \\&=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j(x^{(i)})^Tx^{(j)}-b\sum_{i=1}^m\alpha_iy^{(i)} \tag{5} \end{align}\]

我们定义如下内积符号\(\langle x,y\rangle=x^Ty\)，并将公式4代入公式5可得：

\[\mathcal{L}(w,b,\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle\]

最终我们得到如下对偶优化问题：

\[\begin{align} &\operatorname{max}_\alpha & & W(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^my^{(i)}y^{(j)}\alpha_i\alpha_j\langle x^{(i)},x^{(j)}\rangle\\ &\operatorname{s.t.}& & \alpha_i\ge 0,i=1,\dots,m\\ & & & \sum_{i=1}^m\alpha_iy^{(i)}=0 \end{align}\]

这个对偶问题的求解，留在后面的章节。这里只讨论求解出\(\alpha^*\)之后的情况。

首先，根据公式3可求解\(w^*\)。然后

\[b^*=-\frac{\max_{i:y^{(i)}=-1}w^{*T}x^{(i)}+\min_{i:y^{(i)}=1}w^{*T}x^{(i)}}{2}\]

除此之外，我们还有：

\[w^Tx+b=\left(\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)}\right)^Tx+b=\sum_{i=1}^m\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b\]

在之前的讨论中，我们已经指出只有支持向量对应的\(\alpha_i\)才为非零值，因此：

\[w^Tx+b=\sum_{i\in SV}\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b\]

从上式可以看出，在空间维数比较高的情况下，SVM（support vector machines）可以有效降低计算量。

核函数

假设我们从样本点的分布中看到x和y符合3次曲线，那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维\((x,x^2,x^3)\) ，然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射（feature mapping）。

映射函数记作\(\phi(x)\)，在这个例子中

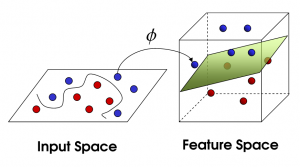
\[\phi(x)=\begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix}\]

有的时候，我们希望将特征映射后的特征，而不是最初的特征，应用于SVM分类。这样做的情况，除了上面提到的拟合问题之外，还在于样例可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。如下图所示：

为此，我们给出核函数（Kernel）的形式化定义：

\[K(x,z)=\phi(x)^T\phi(z)\]

之所以是形式化定义，这主要在于我们并不利用\(\phi(x)\)来计算\(K(x,z)\)，而是给定K(x,z)，来倒推\(\phi(x)\)，从而建立\(\phi(x)\)和\(K(x,z)\)之间的对应关系。

例如：

\[\begin{align}K(x,z)&=(x^Tz)^2=\left(\sum_{i=1}^nx_iz_i\right)\left(\sum_{i=1}^nx_iz_i\right) \\&=\sum_{i=1}^n\sum_{j=1}^nx_ix_jz_iz_j=\sum_{i,j=1}^n(x_ix_j)(z_iz_j) \end{align}\]

根据上式可得：（这里假设\(n=3\)）

\[\phi(x)=\begin{bmatrix} x_1x_1 \\ x_1x_2 \\ x_1x_3 \\ x_2x_1 \\ x_2x_2 \\ x_2x_3 \\ x_3x_1 \\ x_3x_2 \\ x_3x_3 \\ \end{bmatrix}\]

可以看出\(\phi(x)\)的计算复杂度是\(O(n^2)\)，而\((x^Tz)^2\)的计算复杂度是\(O(n)\)。

下面我们讨论其他几种常用核函数和它对应的\(\phi(x)\)。

\[\begin{align}K(x,z)&=(x^Tz+c)^2 \\&=\sum_{i,j=1}^n(x_ix_j)(z_iz_j)+\sum_{i=1}^n(\sqrt{2c}x_i)(\sqrt{2c}z_i)+c^2 \end{align}\]

同样的：（\(n=3\)）

\[\phi(x)=\begin{bmatrix} x_1x_1 \\ x_1x_2 \\ x_1x_3 \\ x_2x_1 \\ x_2x_2 \\ x_2x_3 \\ x_3x_1 \\ x_3x_2 \\ x_3x_3 \\ \sqrt{2c}x_1 \\ \sqrt{2c}x_2 \\ \sqrt{2c}x_3 \\ c \end{bmatrix}\]

更一般的，对于\(K(x,z)=(x^Tz+c)^d\)，其对应的\(\phi(x)\)是\(\begin{bmatrix} n+d \\ d \\ \end{bmatrix}\)维向量。

我们也可以从另外的角度观察\(K(x,z)=\phi(x)^T\phi(z)\)。从内积的几何意义来看，如果\(\phi(x)\)和\(\phi(z)\)夹角越小，则\(K(x,z)\)的值越大；反之，如果\(\phi(x)\)和\(\phi(z)\)的夹角越接近正交，则\(K(x,z)\)的值越小。因此，\(K(x,z)\)也叫做\(\phi(x)\)和\(\phi(z)\)的余弦相似度。