ML » 机器学习（四）——朴素贝叶斯方法
2016-08-17 :: 5767 Words互不相容事件、独立事件与条件独立事件
如果\(P(AB)=0\)，则事件A、B为互不相容事件。
如果\(P(AB)=P(A)P(B)或P(A)=P(A\mid B)\)，则事件A、B为独立事件。
如果\(P(AB\mid R)=P(A\mid R)P(B\mid R)\)，则事件A、B为条件R下的独立事件。
可见，这三者是完全不同的数学概念，不要搞混了。
朴素贝叶斯方法
这里以文本分析（Text Classification）为例，讲解一下朴素贝叶斯（Naive Bayes）方法。
文本分析的一个常用方法是根据词典建立特征向量x。x中的每个元素代表词典里的一个单词，如果该单词在文本中出现，则对应的元素值为1,否则为0。
这里假设我们的目标是通过文本分析，判别一个email是否是垃圾邮件。\(y=1\)表示是垃圾邮件，\(y=0\)表示不是垃圾邮件。显然，在这里一封邮件就是一个样本集。
相比之前的应用领域，文本分析的特殊之处在于词典中的单词数量十分庞大，从而导致x的维数巨大（比如50000个单词，就是50000维），以至于之前的方法，根本无法计算。
为了简化问题，我们假设\(p(x_i\mid y)\)是条件独立的。这个假设被称为朴素贝叶斯假设（Naive Bayes (NB) assumption）。使用这个假设的算法被称为朴素贝叶斯分类器（Naive Bayes classifier）。
从数学角度，NB假设是个很严格的条件，但是实际使用中，即使样本集不满足NB假设，使用NB方法的效果一般还是不错的。
\[\begin{align}p(x_1,\dots,x_{50000}\mid y)&=p(x_1\mid y)p(x_2\mid y,x_1)p(x_3\mid y,x_1,x_2)\cdots p(x_{50000}\mid y,x_1,\dots,x_{49999})(条件概率的乘法公式) \\&=p(x_1\mid y)p(x_2\mid y)p(x_3\mid y)\cdots p(x_{50000}\mid y)(NB假设)=\prod_{i=1}^np(x_i\mid y) \end{align}\]因此：
\[\begin{align}p(y=1\mid x)&=\frac{p(x\mid y=1)p(y=1)}{p(x)} \\&=\frac{(\prod_{i=1}^np(x_i\mid y=1))p(y=1)}{(\prod_{i=1}^np(x_i\mid y=1))p(y=1)+(\prod_{i=1}^np(x_i\mid y=0))p(y=0)}\tag{1} \end{align}\]最大似然估计值为：
\[\phi_{j\mid y=1}=p(x_j=1\mid y=1)=\frac{\sum_{i=1}^m1\{x_j^{(i)}=1\land y^{(i)}=1\}}{\sum_{i=1}^m1\{y^{(i)}=1\}}\] \[\phi_{j\mid y=0}=p(x_j=1\mid y=0)=\frac{\sum_{i=1}^m1\{x_j^{(i)}=1\land y^{(i)}=0\}}{\sum_{i=1}^m1\{y^{(i)}=0\}}\] \[\phi_y=p(y=1)=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}}{m}\]NB算法还可以扩展到y有多个取值的情况。对于y为连续函数的情况，可以采用区间离散化操作，将之离散化为多个离散值。
参考：
https://mp.weixin.qq.com/s/e5Sa66HZly2N0sCqoYNSeA
一文读懂贝叶斯分类算法
https://mp.weixin.qq.com/s/xNZ0x3_o77C1KL1WTdYkfQ
解读实践中最广泛应用的分类模型：朴素贝叶斯算法
https://mp.weixin.qq.com/s/KNV0KfWktmsPUtQ93a7cDQ
这个男人嫁还是不嫁？懂点朴素贝叶斯(Naive Bayes)原理让你更幸福
https://mp.weixin.qq.com/s/ph5KbDxS7QR3I_ev-Js2RQ
朴素贝叶斯文本分类实战
https://mp.weixin.qq.com/s/MfzqlQJedEkCLbh2Mb88Jw
算法工程师必备的机器学习–贝叶斯分类器
拉普拉斯平滑
对于样本集中未出现的单词，在其首次出现时，由于先验概率\(p(x_i\mid y=1)=0,p(x_i\mid y=0)=0\)，这时公式1会出现\(\frac{0}{0}\)的情况。
为了避免这种情况，我们假定先验概率至少为1次，也就是
\[\phi_j=p(y=j)=\frac{\sum_{i=1}^m1\{y^{(i)}=j\}+1}{m+k}\]这种方法叫做拉普拉斯平滑（Laplace Smoothing）。注意这里\(\phi\)的定义和上面略有不同，上面的公式中，y是二值分布，而这里是多值分布（值为k）。为了满足概率和为1的条件，分母上需要加k。
参考：
https://mp.weixin.qq.com/s/_wuE3-7nWyz7VDWdDPJSeQ
一文理解朴素贝叶斯分类的拉普拉斯平滑
文本分类的事件模型
文本分类的事件模型有两类：
1.多值伯努利事件模型（multi-variate Bernoulli event model）。
在这个模型中，我们首先随机选定了邮件的类型（垃圾或者普通邮件，也就是\(p(y)\)），然后翻阅词典，随机决定一个词是否要在邮件中出现，出现则\(x_i\)标示为1，否则标示为0。然后将出现的词，组成一封邮件。一个词是否出现的概率为\(p(x_i\mid y)\)，整封邮件的概率为\(p(y)\prod_{i=1}^np(x_i\mid y)\)。
2.多项事件模型（multinomial event model）。
令\(x_i\)表示邮件的第i个词在字典中的位置，那么\(x_i\)的取值范围为\({1,2,...\lvert V\rvert}\)，\(\lvert V\rvert\)表示字典中单词的数目。这样一封邮件可以表示成\((x_1,x_2,\dots,x_n)\)，这里n为邮件包含的单词个数，显然每个邮件的n值一般是不同的。
这相当于重复投掷\(\lvert V\rvert\)面的骰子，将观察值记录下来就形成了一封邮件。每个面的概率服从\(p(x_i\mid y)\)，而且每次试验条件独立。这样我们得到的邮件概率是\(p(y)\prod_{i=1}^np(x_i\mid y)\)。
需要注意的是，上面两个事件模型的概率公式虽然一致，但含义却有很大差异，不要弄混了。
SVM
支持向量机（SVM，Support Vector Machines）是目前最好的监督学习算法。它由Vladimir Naumovich Vapnik与Alexey Ya. Chervonenkis于1963年提出。
Vladimir Naumovich Vapnik，1936年生，乌兹别克国立大学学士，莫斯科控制科学学院博士，后成为该学院计算机科学研究部门负责人。1990年代末移民美国，先后供职于AT&T Bell、NEC、Facebook，伦敦大学和哥伦比亚大学教授。
Alexey Yakovlevich Chervonenkis，1938～2014，俄罗斯数学家。俄罗斯科学院院士，伦敦大学教授。
我们首先来看一幅图：
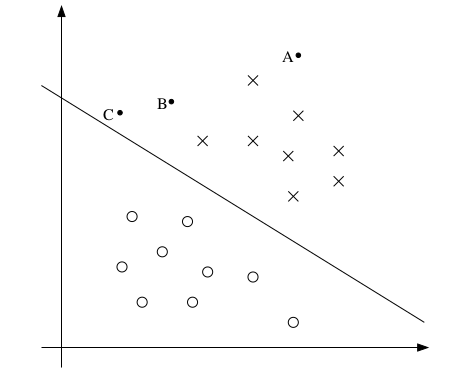
上图中的x和o分别代表y的两种不同取值（1和0）。前面提到逻辑回归的预测函数为\(h_\theta(x)=g(\theta^Tx)\)，那么图中直线的解析方程就是\(\theta^Tx=0\)。这条直线被称作分割超平面（Separating Hyperplane），也就是预测值的分界线。
图中的三个点A、B、C，虽然都在线的上方，然而从直觉来说，A离分界线最远，我们对它的值为1的信心也最足。反观C点，由于离分界线比较近，我们对其值的预测，实际上并没有多大把握。因为这种情况下，样本集的少许调整，就会导致分界线的移动，从而导致预测值的改变。B点的情况介于A和C之间。
和逻辑回归不同，SVM更关心靠近分界线的点，让他们尽可能地远离分界线，而不是在所有点上都达到最优。
为了便于后续讨论，我们对\(h_\theta(x)\)进行改写：\(h_{w,b}(x)=g(w^Tx+b)\)。其中b为常数项，即\(x_0\)的系数项，w为其余的\(x_i\)的系数项。
同时对\(g(z)\)的定义也调整为：
\[g(z)=\begin{cases} 1, & z\ge 0 \\ -1, & z<0 \\ \end{cases}\]这个定义的好处在于\(g(z)\)的取值，只和z的符号相关，而和其绝对值的大小无关。
函数边距和几何边距
为了定义样本点和边界线的距离，我们引入函数边距（functional margin）和几何边距（geometric margins）的定义。
函数边距的定义如下：
\[\hat\gamma=\min_{i=1,\dots,m}\hat\gamma^{(i)},\hat\gamma^{(i)}=y^{(i)}(w^Tx^{(i)}+b)\]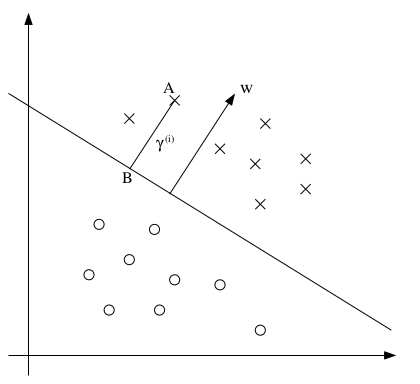
几何边距的几何意义如上图所示。w是分界线的法向量，A的坐标是\(x^{(i)}\)，它到分界线的距离是\(\gamma^{(i)}\)，根据解析几何知识可知，A到分界线的垂足B的坐标为\(x^{(i)}-\gamma^{(i)}\frac{w}{\|w\|}\)。将其代入分界线方程\(w^Tx+b=0\)，可得：
\[w^T\left(x^{(i)}-\gamma^{(i)}\frac{w}{\|w\|}\right)+b=0\Rightarrow w^Tx^{(i)}-\gamma^{(i)}\frac{w^Tw}{\|w\|}+b=0\] \[\Rightarrow w^Tx^{(i)}+b=\gamma^{(i)}\frac{\|w\|^2}{\|w\|}\Rightarrow \gamma^{(i)}=\frac{w^Tx^{(i)}+b}{\|w\|}=\left(\frac{w}{\|w\|}\right)^Tx^{(i)}+\frac{b}{\|w\|}\]这是A在边界线上方时的情况，扩展到整个坐标系的话，上式可改为：
\[\gamma^{(i)}=y^{(i)}\left(\left(\frac{w}{\|w\|}\right)^Tx^{(i)}+\frac{b}{\|w\|}\right)\]同理，可得几何边距的定义为：
\[\gamma=\min_{i=1,\dots,m}\gamma^{(i)}\]从函数边距和几何边距的定义可以看出，如果等比例缩放w和b的话，其几何边距不变，且当\(\|w\|=1\)时，函数边距和几何边距相等。
最优边距分类
SVM算法的本质，就是求能使几何边距最大的w和b的取值，用数学语言描述就是求解问题：
\[\begin{align} &\operatorname{max}_{\gamma,w,b}& & \gamma\\ &\operatorname{s.t.}& & y^{(i)}(w^Tx^{(i)}+b)\ge\gamma,i=1,\dots,m\\ & & & \|w\|=1 \end{align}\]上式中的\(\operatorname{s.t.}\)是subject to的缩写，表示极值问题的约束条件。
这个问题等价于:
\[\begin{align} &\operatorname{max}_{\gamma,w,b}& & \frac{\hat\gamma}{\|w\|}\\ &\operatorname{s.t.}& & y^{(i)}(w^Tx^{(i)}+b)\ge\hat\gamma,i=1,\dots,m \end{align}\]如果能通过比例变换使\(\hat\gamma=1\)，则问题化解为：
\[\begin{align} &\operatorname{min}_{\gamma,w,b}& & \frac{1}{2}\|w\|^2\\ &\operatorname{s.t.}& & y^{(i)}(w^Tx^{(i)}+b)\ge 1,i=1,\dots,m \end{align}\]这个问题实际上就是数学上的QP（Quadratic Programming）问题，采用这种方案的分类被称为最优边距分类（optimal margin classifier）。
拉格朗日对偶
QP问题是有约束条件的优化问题（constrained optimization problem）的一种，下面让我们讨论一下解决这类问题的通用方法。
假设我们求解如下问题：
\[\begin{align} &\operatorname{min}_w& & f(w)\\ &\operatorname{s.t.}& & g_i(w)\le 0,i=1,\dots,k\\ & & & h_i(w)=0,i=1,\dots,l \end{align}\]这里将约束条件分为两类：
1.\(h_i(w)=0\)代表的是约束条件为等式的情况。
2.\(g_i(w)\le 0\)代表的是约束条件为不等式的情况。
您的打赏，是对我的鼓励
