• 广义线性模型
• 生成学习算法
  • 高斯分布的向量形式
  • 矩阵行列式计算
  • 高斯判别分析
  • GDA vs 逻辑回归

广义线性模型

广义线性模型（Generalized Linear Model，GLM）是解决指数类分布的回归问题的通用模型。

它的建模过程如下：

1.首先弄清楚y服从什么分布：

\[y\mid x;\theta \sim ExponentialFamily(\eta) \tag{1}\]

2.为参数\(\eta\)设置linear predictor：

\[\eta=\theta^Tx \tag{2}\]

公式2实际上就是通常意义上的线性模型，即simple linear model。

3.寻找一个合适的link function，将Y的均值映射到linear predictor上，使得：

\[g(h(x))=\eta \tag{3}\]

其中，\(h(x)=E[T(y)\mid x]\)

可见，上一节中的\(\eta\)实际上就是link function。

从上一节的推导还可看出，simple linear model对应的是高斯分布，而其他分布则需要link function进行扩展，这也是广义线性模型得名的由来。

下面以多项分布为例展示一下GLM的处理方法。

\(y\)的取值为\(k\)个离散值的分布，被称为\(k\)项分布。显然\(k=2\)时，就是二项分布了。

这里将\(k\)个离散值出现的概率记作\(\phi_1,\dots,\phi_k\)。由于\(\sum_{i=1}^k=1\)，因此，\(k\)项分布的自由度为\(k-1\)。

定义\(k-1\)维空间上的向量\(T(y)\)：

\[T(1)=\begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, T(2)=\begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, T(k-1)=\begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}, T(k)=\begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}\]

我们使用\((T(y))_i\)表示\(T(y)\)的第\(i\)个元素。

定义函数\(1\{True\}=1,1\{False\}=0\)，则\((T(y))_i=1\{y=i\},E[(T(y))_i]=P(y=i)=\phi_i\)。

\[\begin{align}p(y:\phi)&=\phi_1^{1\{y=1\}}\phi_2^{1\{y=2\}}\cdots \phi_k^{1\{y=k\}}=\phi_1^{1\{y=1\}}\phi_2^{1\{y=2\}}\cdots \phi_k^{1-\sum_{i=1}^{k-1}1\{y=i\}} \\&=\phi_1^{(T(y))_1}\phi_2^{(T(y))_2}\cdots \phi_k^{1-\sum_{i=1}^{k-1}(T(y))_i} \\&=\exp((T(y))_1\log(\phi_1)+(T(y))_2\log(\phi_2)+\cdots+(1-\sum_{i=1}^{k-1}(T(y))_i)\log(\phi_k)) \\&=\exp((T(y))_1\log(\frac{\phi_1}{\phi_k})+(T(y))_2\log(\frac{\phi_2}{\phi_k})+\cdots+(T(y))_{k-1}\log(\frac{\phi_{k-1}}{\phi_k})+\log(\phi_k)) \end{align}\]

可见，

\[\eta=\begin{bmatrix} \log(\frac{\phi_1}{\phi_k}) \\ \log(\frac{\phi_2}{\phi_k}) \\ \vdots \\ \log(\frac{\phi_{k-1}}{\phi_k}) \end{bmatrix},a(\eta)=-\log(\phi_k),b(y)=1\] \[\eta_i=\log(\frac{\phi_i}{\phi_k})\tag{4}\] \[\Rightarrow e^{\eta_i}=\frac{\phi_i}{\phi_k}\Rightarrow \phi_ke^{\eta_i}=\phi_i\] \[\Rightarrow \phi_k\sum_{i=1}^ke^{\eta_i}=\sum_{i=1}^k\phi_i=1\] \[\Rightarrow \phi_k=\frac{1}{\sum_{i=1}^ke^{\eta_i}}\tag{5}\]

由公式4、5可得：

\[\phi_i=\frac{e^{\eta_i}}{\sum_{j=1}^ke^{\eta_j}}=\frac{e^{\theta_i^Tx}}{\sum_{j=1}^ke^{\theta_j^Tx}}\]

这种从\(\eta\)映射到\(\phi\)的函数，被称作softmax函数。

由于softmax函数给出的是分类结果的概率，因此对于某些分类结果中，所有类别概率都很低的情况，我们有理由认为遇到了未知的类别。softmax函数的这种概率可解释性，是它优于其他函数的地方。

\[h_\theta(x)=E[T(y)\mid x;\theta]=\begin{bmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_{k-1} \end{bmatrix} =\begin{bmatrix} \frac{\exp(\theta_1^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)} \\ \frac{\exp(\theta_2^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)} \\ \vdots \\ \frac{\exp(\theta_{k-1}^Tx)}{\sum_{j=1}^k\exp(\theta_j^Tx)} \end{bmatrix}\]

最大似然估计对数函数：

\[\ell(\theta)=\sum_{i=1}^m\log p(y^{(i)}\mid x^{(i)};\theta)=\sum_{i=1}^m\log\prod_{l=1}^k\left(\frac{\exp(\theta_{l}^Tx^{(i)})}{\sum_{j=1}^k\exp(\theta_j^Tx^{(i)})}\right)^{1\{y^{(i)}=l\}}\]

参考：

http://statmath.wu.ac.at/courses/heather_turner/

INTRODUCTION TO GENERALIZED LINEAR MODELS

https://mp.weixin.qq.com/s/jeloJDgfa3eFXUPduhesVA

logistic函数和softmax函数

https://mp.weixin.qq.com/s/iGJ7Xt4_QSZOC0fG0yJfhg

从最大似然估计开始，你需要打下的机器学习基石

生成学习算法

比如说，要确定一只羊是山羊还是绵羊。从历史数据中学习到模型，然后通过提取这只羊的特征，来预测出这只羊是山羊还是绵羊。这种方法叫做判别学习算法（DLA，Discriminative Learning Algorithm）。其形式化的写法是：\(p(y\mid x)\)。

换一种思路，我们可以根据山羊的特征首先学习出一个山羊模型，然后根据绵羊的特征学习出一个绵羊模型。然后从这只羊中提取特征，放到山羊模型中看概率是多少，再放到绵羊模型中看概率是多少，哪个大就是哪个。这种方法叫做生成学习算法（GLA，Generative Learning Algorithms）。其形式化的写法是：建立模型——\(p(x\mid y)\)，应用模型——\(p(y)\)。

由贝叶斯（Bayes）公式可知：

\[p(y\mid x)=\frac{p(x\mid y)p(y)}{p(x\mid y=1)p(y=1)+p(x\mid y=0)p(y=0)}=\frac{p(x\mid y)p(y)}{p(x)} \tag{6}\]

其中，\(p(x\mid y)\)称为后验概率，\(p(y)\)称为先验概率。

Thomas Bayes，1701~1761，英国统计学家。

由于我们关注的是y的离散值结果中哪个概率大（比如山羊概率和绵羊概率哪个大），而并不是关心具体的概率，因此公式6可改写为：

\[\arg\max_yp(y\mid x)=\arg\max_y\frac{p(x\mid y)p(y)}{p(x)}=\arg\max_yp(x\mid y)p(y) \tag{7}\]

先验/后验概率还可从参数估计的角度来考虑：

\[p(\theta\mid x)=\frac{p(x\mid \theta)p(\theta)}{p(x)}\]

这里的\(\theta\)表示模型的参数。先验概率是根据经验设定的参数值，后验概率是样本实测值，代入Bayes公式即可得到参数的真实值。

常见的判别式模型有Logistic Regression，Linear Regression，SVM，Traditional Neural Networks，Nearest Neighbor，CRF等。

常见的生成式模型有Naive Bayes，Mixtures of Gaussians， HMMs，Markov Random Fields等。

判别式模型，优点是分类边界灵活，学习简单，性能较好；缺点是不能得到概率分布。

生成式模型，优点是收敛速度快，可学习分布，可应对隐变量；缺点是学习复杂，分类性能较差。

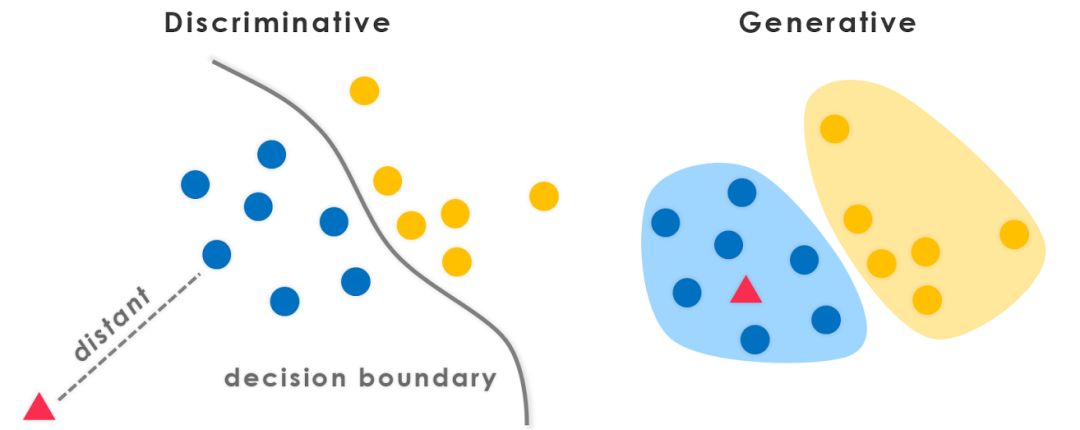
上面是一个分类例子，可知判别式模型，有清晰的分界面，而生成式模型，有清晰的概率密度分布，也就是所谓的生成label的能力。生成式模型，可以转换为判别式模型，反之则不能。

参考：

https://zhuanlan.zhihu.com/p/42726550

为什么要对参数设先验(Prior)

https://mp.weixin.qq.com/s/6_BSs7SK2HWq0-7RgNeuzA

理解生成模型与判别模型

https://zhuanlan.zhihu.com/p/37768413

小白之通俗易懂的贝叶斯定理（Bayes’ Theorem）

高斯分布的向量形式

高斯分布的向量形式\(N(\mu,\Sigma)\)的概率密度函数为：

\[p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)\]

其中，\(\mu\)表示均值向量（Mean Vector），\(\Sigma\)表示协方差矩阵（Covariance Matrix），\(\lvert\Sigma\rvert\)表示协方差矩阵的行列式。

矩阵行列式计算

对于高阶矩阵行列式，一般采用莱布尼茨公式（Leibniz Formula）或拉普拉斯公式（Laplace Formula）计算。

首先，定义排列A的反序向量V（Inversion Vector）。下面举一个包含6个元素的例子：

序列	4 1 5 2 6 3
反序向量	0 1 0 2 0 3

\[V_i=\sum_{j=1}^{i-1}f(i,j), f(i,j)=\begin{cases} 1, & A_i<A_j \\ 0, & A_i>A_j \\ \end{cases}\]

反序向量的模被称为总序数（Total Order），例如上面例子的总序数为\(1+2+3=6\)。

总序数为奇数的排列被称为奇排列（Odd Permutations），为偶数的排列被称为偶排列（Even Permutations）。

定义勒维奇维塔符号(Levi-Civita symbol)如下：

\[\varepsilon_{a_1 a_2 a_3 \ldots a_n} = \begin{cases} +1 & \text{if }(a_1 , a_2 , a_3 , \ldots , a_n) \text{ is an even permutation of } (1,2,3,\dots,n) \\ -1 & \text{if }(a_1 , a_2 , a_3 , \ldots , a_n) \text{ is an odd permutation of } (1,2,3,\dots,n) \\ 0 & \text{otherwise} \end{cases}\]

Tullio Levi-Civita，1873~1941，意大利数学家。他在张量微积分领域的贡献，帮助了相对论的确立。

莱布尼茨公式：

\[\det(A) = \sum_{i_1,i_2,\ldots,i_n=1}^n \varepsilon_{i_1\cdots i_n} a_{1,i_1} \cdots a_{n,i_n}\]

高斯判别分析

高斯判别分析（GDA，Gaussian Discriminant Analysis）模型需要满足以下条件：

\[y\sim Bernoulli(\phi)\] \[x\mid y=0\sim N(\mu_0,\Sigma)\] \[x\mid y=1\sim N(\mu_1,\Sigma)\]

这里只讨论y有两种分类的情况，且假设两种分类的\(\Sigma\)相同。

相应的概率密度函数为：

\[p(y)=\phi^y(1-\phi)^{1-y}\] \[p(x\mid y=0)=\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_0)^T\Sigma^{-1}(x-\mu_0)\right)=\frac{1}{A}\exp(f(\mu_0,\Sigma,x))\] \[p(x\mid y=1)=\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\right)=\frac{1}{A}\exp(f(\mu_1,\Sigma,x))\]

将上面三个分布的概率密度函数代入《机器学习（二）》公式7，可求得\(\arg\max_yp(y\mid x)\)，然后进行最大似然估计，可得该GDA的最大似然估计参数为：（过程略）

\[\phi=\frac{1}{m}\sum_{i=1}^m1\{y^{(i)}=1\}\] \[\mu_0=\frac{\sum_{i=1}^m1\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^m1\{y^{(i)}=0\}}\] \[\mu_1=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^m1\{y^{(i)}=1\}}\] \[\Sigma=\frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T\]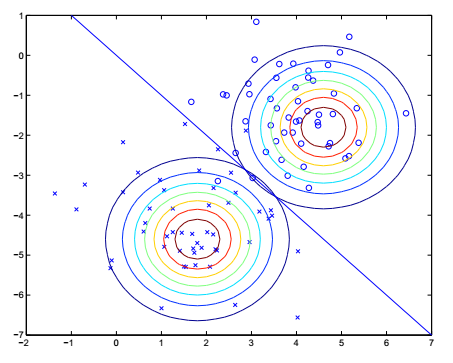

上图中的直线就是分界线\(p(y=1\mid x)=0.5\)。

GDA vs 逻辑回归

\[\begin{align}p(y=1\mid x)&=\frac{p(x\mid y=1)p(y=1)}{p(x\mid y=1)p(y=1)+p(x\mid y=0)p(y=0)} \\&=\frac{\frac{1}{A}\exp(f(\mu_0,\Sigma,x))\phi}{\frac{1}{A}\exp(f(\mu_0,\Sigma,x))\phi + \frac{1}{A}\exp(f(\mu_1,\Sigma,x))(1-\phi)} \\&=\frac{1}{1+\frac{\exp(f(\mu_1,\Sigma,x))(1-\phi)}{\exp(f(\mu_0,\Sigma,x))\phi}} \\&=\frac{1}{1+\exp(f(\mu_1,\Sigma,x)+\log(1-\phi)-f(\mu_0,\Sigma,x)-\log(\phi))} \\&=\frac{1}{1+\exp(-\theta^Tx)} \end{align}\]

从上面的变换可以看出，GDA是逻辑回归的特例。

一般来说，GDA的条件比逻辑回归严格。因此，如果模型符合GDA的话，采用GDA方法，收敛速度（指所需训练集的数量）比较快。

而逻辑回归的鲁棒性较好，对于非GDA模型或者模型不够准确的情况，仍能收敛。