DL » 深度学习(三十三)——Capsule
2018-01-25 :: 6062 WordsCapsule
Capsule是深度学习先驱Hinton于2017年提出的概念。
论文:
《Dynamic Routing Between Capsules》
《Matrix capsules with EM Routing》
《Stacked Capsule AutoEncoder》
官方代码:
https://github.com/Sarasra/models/tree/master/research/capsules
2023.6
经过了6年实践,Capsule和周志华的深度树学习,基本已经被扫进了垃圾堆。。。囧
讲述Capsule的blog已经有很多了,但论通俗易懂,还得是苏剑林的这三篇blog:
http://kexue.fm/archives/4819/
揭开迷雾,来一顿美味的“Capsule”盛宴
https://kexue.fm/archives/5112/
再来一顿贺岁宴:从K-Means到Capsule
https://kexue.fm/archives/5155/
三味Capsule:矩阵Capsule与EM路由
老规矩,这里依旧是整理摘要。
何为Capsule?
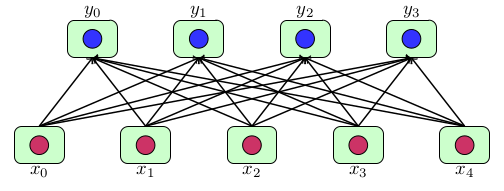
上图是FC的示意图。其中的\(x_i,y_i\)都是标量,可以被看作是某个特征的值。
公式化的表示如下:
\[\boldsymbol{x}\in\mathbb{R}^n,\boldsymbol{y}=Activation(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})\in \mathbb{R}^k\]但是,实际问题中,特征的值不见得全是标量,也有可能是矢量。
比如下面的文章就讨论了\(x_i\)是复数,也就是二维矢量的情况:
https://mp.weixin.qq.com/s/UMi5NUqcqNTBjlt946jFFQ
深度学习应该使用复数吗?
Hinton当然不满足于此,他将特征的值推广到多维,也就引出了Capsule的概念。
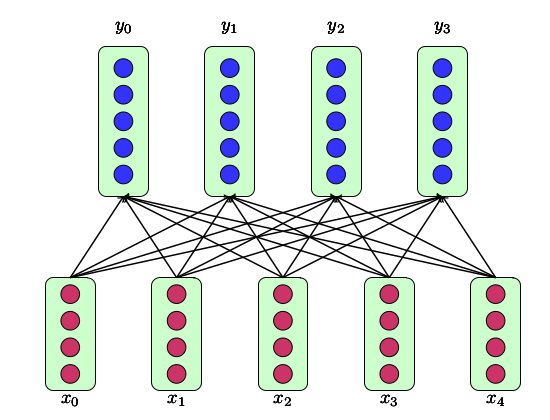
上图中的\(x_i\)是一个矢量,它被Hinton称之为Capsule。
公式化的表示如下:
\[\boldsymbol{x}\in\mathbb{R}^{n\times d_x}, \boldsymbol{y}=Routing(\boldsymbol{x})\in \mathbb{R}^{k\times d_y}\]细心的读者,应该已经发现了,普通FC中的Activation,在这里被换成了Routing。
那么,这些胶囊要怎么运算呢?
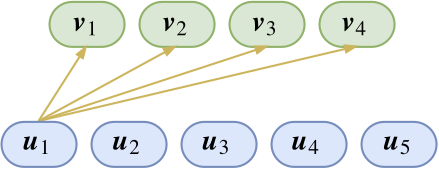
我们先留心观察capsule的一部分连接。目前已经有了\(u_1\)这个特征(假设是羽毛),那么我想知道它属于上层特征\(v_1,v_2,v_3,v_4\)(假设分别代表了鸡、鸭、鱼、狗)中的哪一个。分类问题我们显然已经是很熟悉了,不就是内积后softmax吗?于是单靠\(u_1\)这个特征,我们推导出它是属于鸡、鸭、鱼、狗的概率分别是:
\[\big(p_{1\mid 1},p_{2\mid 1},p_{3\mid 1},p_{4\mid 1}\big) = \frac{1}{Z_1}\Big(e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_1\rangle}, e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_2\rangle}, e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_1\rangle}, e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_1\rangle}\Big)\]我们当然期望\(p_{1\mid 1}\)和\(p_{2\mid 1}\)会明显大于\(p_{3\mid 1}\)和\(p_{4\mid 1}\)。不过,单靠这个特征还不够,我们还需要综合各个特征,于是可以把上述操作对各个\(u_i\)都做一遍,继而得到\(\big(p_{1\mid 2},p_{2\mid 2},p_{3\mid 2},p_{4\mid 2}\big),\big(p_{1\mid 3},p_{2\mid 3},p_{3\mid 3},p_{4\mid 3}\big),\dots\)
Hinton认为,既然\(u_i\)这个特征得到的概率分布是\(\big(p_{1\mid i},p_{2\mid i},p_{3\mid i},p_{4\mid i}\big)\),那么我把这个特征切成四份,分别为\(\big(p_{1\mid i}\boldsymbol{u}_i,p_{2\mid i}\boldsymbol{u}_i,p_{3\mid i}\boldsymbol{u}_i,p_{4\mid i}\boldsymbol{u}_i\big)\),然后把这几个特征分别传给\(v_1,v_2,v_3,v_4\),最后\(v_1,v_2,v_3,v_4\)其实就是各个底层传入的特征的累加,即:
\[\boldsymbol{v}_j = squash\left(\sum_{i} p_{j\mid i} \boldsymbol{u}_i\right) = squash\left(\sum_{i} \frac{e^{\langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle}}{Z_i} \boldsymbol{u}_i\right)\tag{1}\]从上式括号中的部分可以看出,\(v_j\)实际上就是所有\(u_i\)的加权平均,这实际上就是一种类似K-Means的聚类。因此,Capsule的核心思想就是输出是输入的某种聚类的结果。
squash与聚类
使用何种规则进行聚类呢?Hinton给出了如下squash函数:
\[squash(\boldsymbol{x})=\frac{\Vert\boldsymbol{x}\Vert^2}{1+\Vert\boldsymbol{x}\Vert^2}\frac{\boldsymbol{x}}{\Vert\boldsymbol{x}\Vert}\]这个函数的特点是:用模长代表特征的概率,模长越大,这个特征越显著。
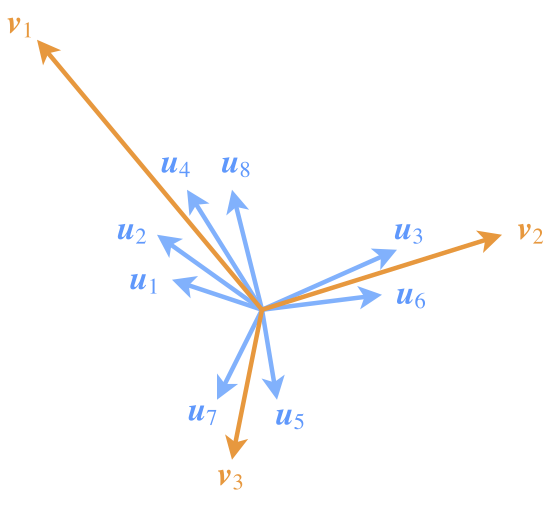
为了突出模长的这一含义,也需要在设计模型的时候有所配合。如图,尽管\(v_1\)所代表的类所包含的特征向量\(u_1,u_2,u_4,u_8\)的模长均比较小,但因为成员多(“小弟多”),因此v1的模长也能占优(“势力大”)。这说明,一个类要突出,跟类内向量的数目、每个类内向量本身的模长都有关联。
苏剑林认为将squash函数中的1,改成0.5,似乎效果更好一些。这个函数的特点是在模长很接近于0时起到放大作用,而不像原来的函数那样全局都压缩。
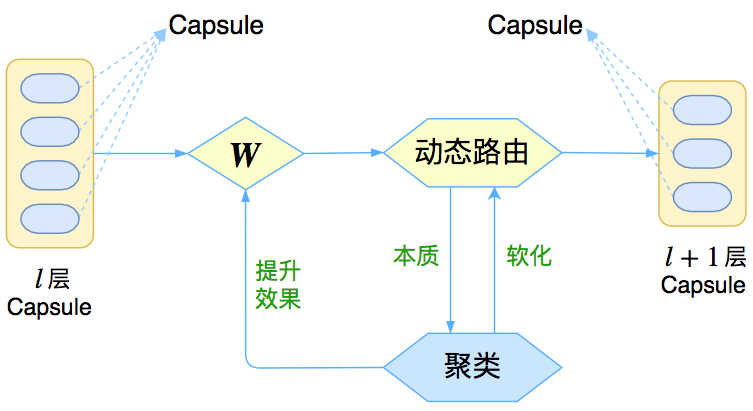
Dynamic Routing
注意到(1)式,为了求\(v_j\)需要求softmax,可是为了求softmax又需要知道\(v_j\),这不是个鸡生蛋、蛋生鸡的问题了吗?这时候就要上“主菜”了,即“动态路由”(Dynamic Routing),它能够根据自身的特性来更新(部分)参数,从而初步达到了Hinton的放弃梯度下降的目标。
我们首先回顾一下最简单的聚类算法K-Means算法是如何解决鸡生蛋、蛋生鸡的问题的。(参见《机器学习(九)》)
答案是迭代算法。由K-Means算法的收敛性可知,这类迭代算法至少可以收敛到一个局部最优解。
具体到Capsule,为了得到各个\(v_j\),一开始先让它们全都等于\(u_i\)的均值,然后反复迭代就好。说白了,输出是输入的聚类结果,而聚类通常都需要迭代算法,这个迭代算法就称为“动态路由”。
至于这个动态路由的细节,其实是不固定的,取决于聚类的算法,比如关于Capsule的新文章《Matrix capsules with EM Routing》就使用了Gaussian Mixture Model来聚类。
K-Means聚类可以采用任意距离,但GMM只能采用欧氏距离,用欧氏距离进行聚类的一个特点就是聚类中心向量是类内向量的(加权)平均,既然是平均,就不能体现“小弟越多,势力越大”的特点。因此,这时的Capsule就变成了如下所示的“一个矩阵+一个标量”:
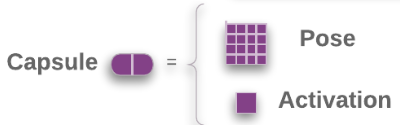
这里的矩阵和原始论文的向量有什么区别呢?
比如一个4×4的矩阵,跟一个16维的向量,有什么差别呢?答案是矩阵的不同位置的元素重要性不一样,而向量的每个元素的重要性都是一样的。熟悉线性代数的读者应该也可以感觉到,一个矩阵的对角线元素的地位“看起来”是比其他元素要重要一些的。从计算的角度看,也能发现区别:要将一个16维的向量变换为另外一个16维的向量,我们需要一个16×16的变换矩阵;但如果将一个4×4的矩阵变换为另外一个4×4的矩阵,那么只需要一个4×4的变换矩阵,参数量减少了。
总结
Capsule的优点
Capsule的可解释性有很大提升,下图是Hinton论文中给出的示例:
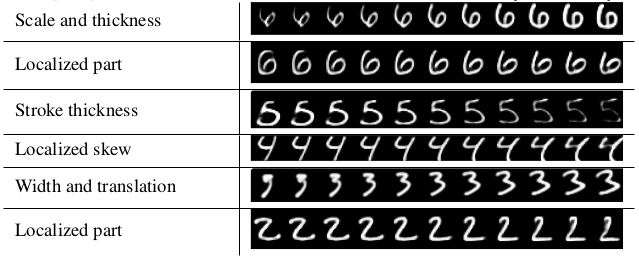
其次,Capsule的鲁棒性也有很大提升,比如下图所示的两个手写字符重叠的情况,传统CNN模型一般是搞不定的。

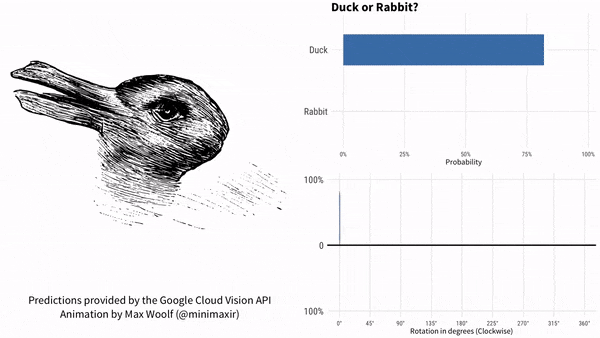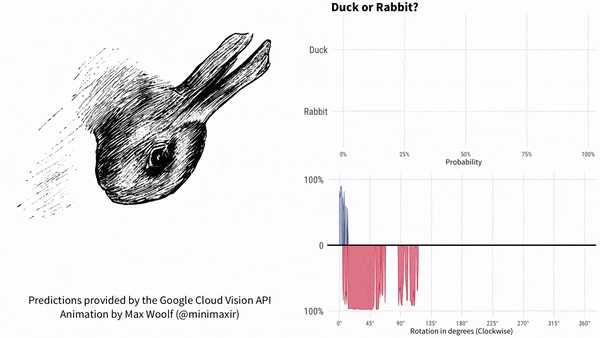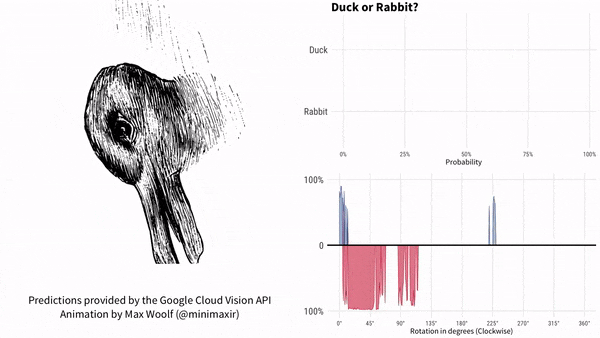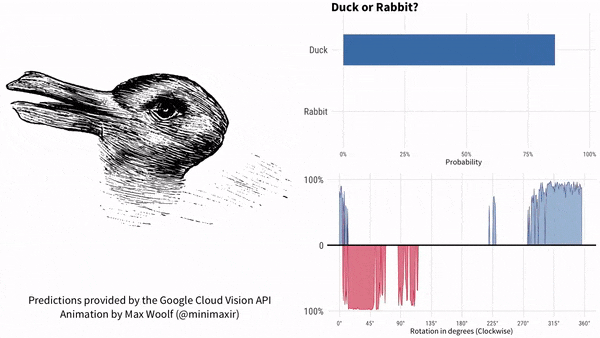
上面这张图,画的是鸭子还是兔子?
自从1892年首次出现在一本德国杂志上之后,这张图就一直持续引发争议。有些人只能看到一只兔子,有些人只能看到一只鸭子,有些人两个都能看出来。
为了搞清楚这件事,供职于BuzzFeed的数据科学家Max Woolf设计了一个更复杂的实验,他干脆让这张图旋转起来,倒是要看看,谷歌AI什么表现。
同一张图片,由于位置不同,AI就产生了不同的判断。也有很多人想到了更多。
传统的卷积神经网络CNN架构中有个弊端,就是缺乏可用的空间信息。
参考
https://mp.weixin.qq.com/s/MEfcdttm73oCxsJKWz6fnw
Capsule Networks,胶囊网络,57页ppt,布法罗大学
https://mp.weixin.qq.com/s/c5gxaOY2ITN-Q-U0mCYNgA
《胶囊网络(Capsule Networks)综述》
https://mp.weixin.qq.com/s/gzCDE6PR8rEs8QEy8Mj00g
胶囊网络与计算机视觉教程
https://www.zhihu.com/question/67287444
如何看待Hinton的论文《Dynamic Routing Between Capsules》?
https://mp.weixin.qq.com/s/p_92_arJBHX6nPCY1wF5cg
Hinton胶囊网络代码正式开源
https://mp.weixin.qq.com/s/TYE8Z9kogXttvWiL81762w
Capsule官方代码开源之后,机器之心做了份核心代码解读
https://mp.weixin.qq.com/s/Tx9JJ0cIo_rH7BDjd_hkvw
Hinton碰撞LeCun:CNN有两大缺陷,要用capsule做下一代CNN
https://zhuanlan.zhihu.com/p/29435406
浅析Hinton最近提出的Capsule计划
https://mp.weixin.qq.com/s/5Af_K_BGrD5RomgpWxJNBQ
Hinton大神Capsule论文首次公布,深度学习基石CNN或被取代
https://mp.weixin.qq.com/s/wFoRtTKW40qgYmlXY0dRDw
一篇新的Capsule论文:优于基准CNN
https://mp.weixin.qq.com/s/9Vqg3HkDCfl1qMDIN-eCGQ
Geoffrey Hinton那篇备受关注的Capsule论文公开了
https://mp.weixin.qq.com/s/8U3vFaf3SDCYnWy4lQv6uw
代替反向传播的另一种深度学习算法:离散优化
http://mp.weixin.qq.com/s/gdke9E1A3eRUzgidp9uOqg
邓侃:一文读懂Hinton最新Capsules论文
https://mp.weixin.qq.com/s/R9pDEc7zqZdttLJGCfiv2w
TensorFlow Pytorch Keras代码实现深度学习大神Hinton NIPS2017 Capsule论文
https://mp.weixin.qq.com/s/WspmbqlwdxKXH1cgbkuGwQ
先读懂CapsNet架构然后用TensorFlow实现,这应该是最详细的教程了
https://mp.weixin.qq.com/s/Ot-pRRaHaT1VRyWlLDO2uw
Reddit讨论:Hinton的Capsule网络真的比CNN效果更好吗?
https://mp.weixin.qq.com/s/Z32LCfi8IVP4WXkxAu6zZg
Geffory Hinton的“胶囊”里到底装的什么“药”?
https://mp.weixin.qq.com/s/f0TqhSW-KVwVTv54gtHyGw
胶囊网络9大优势4大缺陷
https://mp.weixin.qq.com/s/0uqS5CXVVxjX2c3P-gdSng
欲取代CNN的Capsule Network究竟是什么来头?
https://mp.weixin.qq.com/s/k3WV7qN37r-r3VBJsrjB1A
漫谈Capsule Network基本原理
https://mp.weixin.qq.com/s/AchyBBTZ3X3zYSM8-9WTrA
Capsule Network在TIMIT语音识别中的实践(一)
https://zhuanlan.zhihu.com/p/30830319
Geoffrey Hinton的CapsNet在云平台上应用
https://mp.weixin.qq.com/s/fZUiAjhSg1pESsVspqaCFQ
胶囊网络是如何克服卷积神经网络的这些缺点的?
https://mp.weixin.qq.com/s/x7SIa4NAczTHcWs6nxP9NQ
胶囊网络(Capsule Network)在文本分类中的探索
https://mp.weixin.qq.com/s/HbqmdaxIQrQc7vDgiExtrw
可视化CapsNet,详解Hinton等人提出的胶囊概念与原理
https://mp.weixin.qq.com/s/VcZSHw98w6nvgz4Hzjto3A
深度学习之CapsuleNets理论与Python实践

您的打赏,是对我的鼓励
