• Normalization进阶（续）
  • Cosine Normalization
  • IBN-Net
  • Group Normalization
  • L2 Normalization
  • Local Response Normalization
  • RMS Normalization
  • DL Regularization
  • 参考
• fine-tuning
• Style Transfer
  • 早期方法

Normalization进阶（续）

Cosine Normalization

Normalization还能怎么做？

我们再来看看神经元的经典变换\(f_w(x)=w\cdot x\)。

对输入数据x的变换已经做过了，横着来是LN，纵着来是BN。

对模型参数w的变换也已经做过了，就是WN。

好像没啥可做的了。然而天才的研究员们盯上了中间的那个点，对，就是\(\cdot\)。

\[f_w(x)=\cos \theta=\frac{w\cdot x}{\|w\|\cdot\|x\|}\]

参考：

https://mp.weixin.qq.com/s/EBRYlCoj9rwf0NQY0B4nhQ

Layer Normalization原理及其TensorFlow实现

http://mlexplained.com/2018/01/10/an-intuitive-explanation-of-why-batch-normalization-really-works-normalization-in-deep-learning-part-1/

An Intuitive Explanation of Why Batch Normalization Really Works

https://mp.weixin.qq.com/s/KnmQTKneSimuOGqGSPy58w

详解深度学习中的Normalization，不只是BN（1）

https://mp.weixin.qq.com/s/nSQvjBRMaBeoOjdHbyrbuw

详解深度学习中的Normalization，不只是BN（2）

https://mp.weixin.qq.com/s/Z119_EpLKDz1TiLXGbygJQ

MIT新研究参透批归一化原理

https://mp.weixin.qq.com/s/Lp2pq95woQ5-E3RemdRnyw

动态层归一化（Dynamic Layer Normalization）

https://zhuanlan.zhihu.com/p/43200897

深度学习中的Normalization模型

IBN-Net

IBN-Net是汤晓鸥小组的新作（2018.7）。

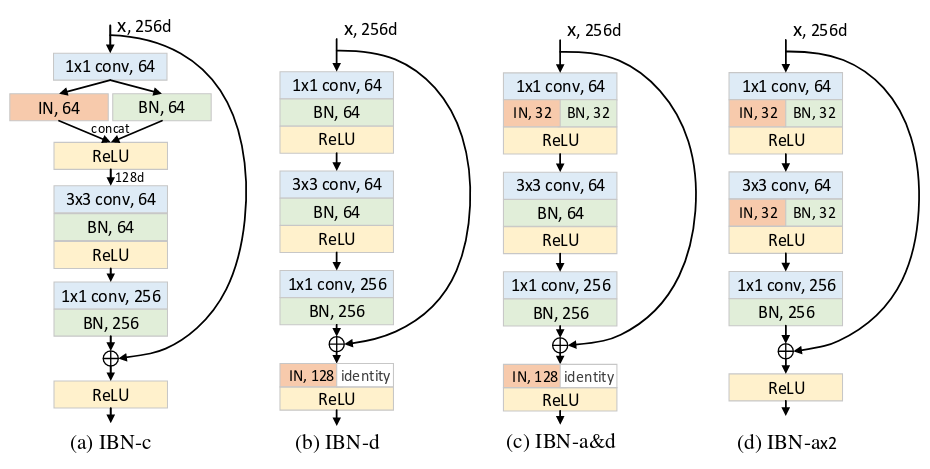
与BN相比，IN有两个主要的特点：第一，它不是用训练批次来将图像特征标准化，而是用单个样本的统计信息；第二，IN能将同样的标准化步骤既用于训练，又用于推断。

潘新钢等发现，IN和BN的核心区别在于，IN学习到的是不随着颜色、风格、虚拟性/现实性等外观变化而改变的特征，而要保留与内容相关的信息，就要用到BN。

论文：

《Two at Once: Enhancing Learning and Generalization Capacities via IBN-Net》

参考：

https://mp.weixin.qq.com/s/LVL90n4–WPgFLMQ-Gnf6g

汤晓鸥为CNN搓了一颗大力丸

https://mp.weixin.qq.com/s/6hNpgffEnUTkNAfrPgKHkA

IBN-Net：打开Domain Generalization的新方式

https://mp.weixin.qq.com/s/lCasw_-Bl3_J6cGBipNsSA

从IBN-Net到Switchable Whitening：在不变性与判别力之间权衡

Group Normalization

论文：

《Group Normalization》

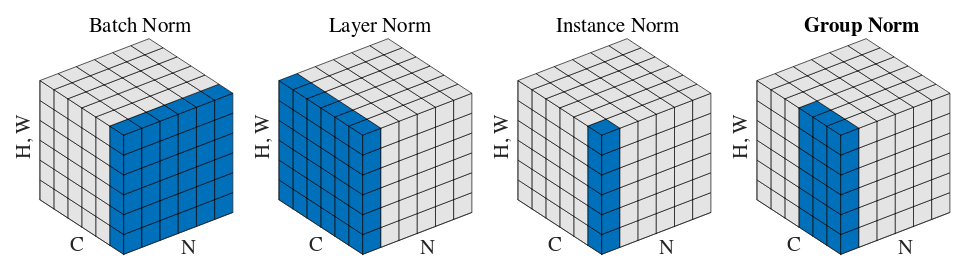
参考：

https://mp.weixin.qq.com/s/H2GmqloNumttFlaSArjgUg

FAIR何恺明等人提出组归一化：替代批归一化，不受批量大小限制

https://mp.weixin.qq.com/s/44RvXEYYc5lebsHs_ooswg

全面解读Group Normalization

https://mp.weixin.qq.com/s/J8i0Qsl0q9sYS2iAc-M44w

BN，LN，IN，GN都是什么？不同归一化方法的比较

L2 Normalization

L2 Normalization本身并不复杂，然而多数资料都只提到1维的L2 Normalization的计算公式：

\[\begin{array}\\ x=[x_1,x_2,\dots,x_d]\\ y=[y_1,y_2,\dots,y_d]\\ y=\frac{x}{\sqrt{\sum_{i=1}^dx_i^2}}=\frac{x}{\sqrt{x^Tx}} \end{array}\]

对于多维L2 Normalization几乎未曾提及，这里以3维tensor：A[width, height, channel]为例介绍一下多维L2 Normalization的计算方法。

多维L2 Normalization有一个叫axis(有时也叫dim)的参数，如果axis=0的话，实际上就是将整个tensor flatten之后，再L2 Normalization。这个是比较简单的。

这里说说axis=3的情况。axis=3意味着对channel进行Normalization，也就是：

\[B_{xy}=\sum_{z=0}^Z \sqrt{A_{xyz}^2}\\ C_{xyz}=\frac{A_{xyz}}{B_{xy}}\\ D_{xyz}=C_{xyz} \cdot S_{z}\]

一般来说，求出C的运算被称作L2 Normalization，而求出D的运算被称作L2 Scale Normalization，S被称为Scale。

Local Response Normalization

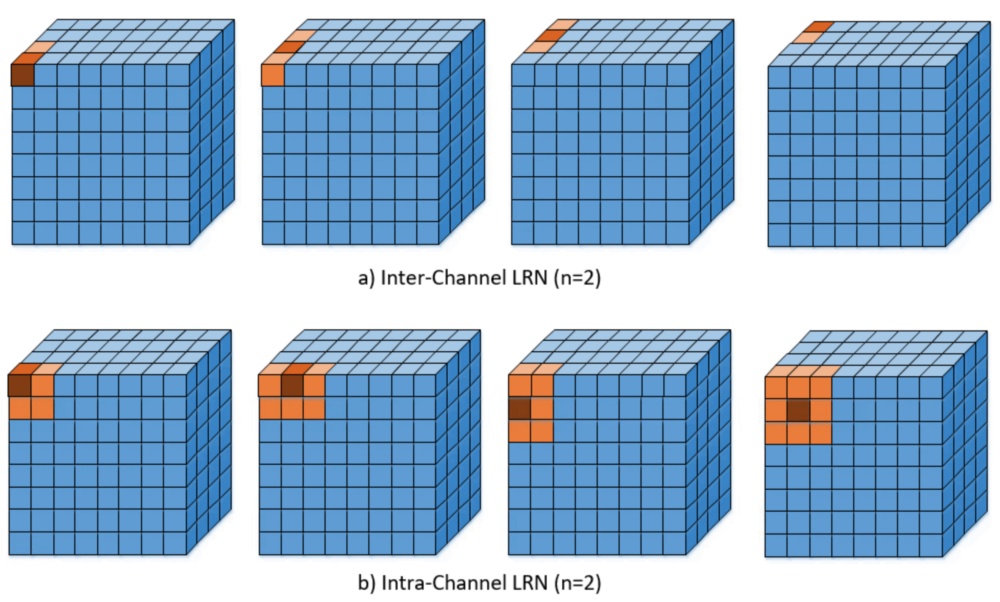
LRN最早出自Alexnet，虽然后来由于效果不佳，已经很少使用了，但它的思路还是可以借鉴的。

LRN分为Inter-Channel LRN和Intra-Channel LRN两种，如果不加说明的话，一般是指前者。

Inter-Channel LRN：

\[b_{x,y}^i=a_{x,y}^i / \left( k+\alpha \sum_{j=\max (0,i-n/2)}^{\min(N-1,i+n/2)}(a_{x,y}^j)^2\right)^\beta\]

其中，\(a_{x,y}^i\)表示feature map第i通道上坐标为x,y的点的值。因此，Inter-Channel LRN的做法就是：将相邻的几个通道上相同坐标的点的值，代入公式，进行Normalization。

这实际上和1x1的卷积比较像，不同之处在于：1x1的卷积处理所有通道，而Inter-Channel LRN只处理相邻通道。

上式中的\(k,n,\alpha,\beta\)均为超参数，N为通道数。显然，如果\((k,\alpha,\beta,n)=(0,1,1,N)\)的话，就是Channel Normalization了。

Intra-Channel LRN：

\[b_{x,y}^k=a_{x,y}^k / \left( k+\alpha \sum_{i=\max (0,x-n/2)}^{\min(W,x+n/2)}\sum_{j=\max (0,y-n/2)}^{\min(H,y+n/2)}(a_{i,j}^k)^2\right)^\beta\]

Intra-Channel LRN和平均池化非常类似，它处理的是W,H上的相邻关系。

参考：

https://mc.ai/difference-between-local-response-normalization-and-batch-normalization/

Difference between Local Response Normalization and Batch Normalization

RMS Normalization

与LayerNorm相比，RMS Norm的主要区别在于去掉了减去均值的部分，计算公式为：

\[\bar{a_i} = \frac{a_i}{\text{RMS}(\mathbf{a})} g_i, \text{where}~ \text{RMS}(\mathbf{a}) = \sqrt{\frac{1}{n} \sum_{i=1}^{n} a_i^2}.\]

g为可训练的参数。

作者认为这种模式在简化了Layer Norm的同时，可以在各个模型上减少约7%∼64%的计算时间。

https://zhuanlan.zhihu.com/p/620297938

Layer Norm、RMS Norm、Deep Norm

DL Regularization

DL中的Regularization除了常见的\(l_1\)-norm、\(l_2\)-norm和squared \(l_2\)-norm之外，还有Group Regularization。它的定义如下：

\[loss(W;x;y) = loss_D(W;x;y) + \lambda_R R(W) + \lambda_g \sum_{l=1}^{L} R_g(W_l^{(G)})\] \[R_g(w^{(g)}) = \sum_{g=1}^{G} \lVert w^{(g)} \rVert_g = \sum_{g=1}^{G} \sum_{i=1}^{|w^{(g)}|} {(w_i^{(g)})}^2\]

Group Regularization也叫做Block Regularization或Structured Regularization。

参考

https://zhuanlan.zhihu.com/p/69659844

如何区分并记住常见的几种Normalization算法

https://mp.weixin.qq.com/s/KYGqSOftm8FWDXk_C13iCQ

Conditional Batch Normalization详解

https://mp.weixin.qq.com/s/w_W4NwkCRdbyZbEwMlrFRQ

超越BN和GN！谷歌提出新的归一化层：FRN

https://mp.weixin.qq.com/s/T5vDmlaVdqvvxtqd1t3lww

Unsupervised Batch Normalization

https://mp.weixin.qq.com/s/f-S_Wgc2B_2oN7Nk-20y8g

正则化与标准化大总结

https://zhuanlan.zhihu.com/p/75539170

神经网络中Normalization的发展历程

https://zhuanlan.zhihu.com/p/340747455

深度学习中眼花缭乱的Normalization学习总结

https://zhuanlan.zhihu.com/p/380620373

BatchNorm避坑指南

fine-tuning

fine-tuning和迁移学习虽然是两个不同的概念。但局限到CNN的训练领域，基本可以将fine-tuning看作是一种迁移学习的方法。

举个例子，假设今天老板给你一个新的数据集，让你做一下图片分类，这个数据集是关于Flowers的。问题是，数据集中flower的类别很少，数据集中的数据也不多，你发现从零训练开始训练CNN的效果很差，很容易过拟合。怎么办呢，于是你想到了使用Transfer Learning，用别人已经训练好的Imagenet的模型来做。

由于ImageNet数以百万计带标签的训练集数据，使得如CaffeNet之类的预训练的模型具有非常强大的泛化能力，这些预训练的模型的中间层包含非常多一般性的视觉元素，我们只需要对他的后几层进行微调，再应用到我们的数据上，通常就可以得到非常好的结果。最重要的是，在目标任务上达到很高performance所需要的数据的量相对很少。

虽然从理论角度尚无法完全解释fine-tuning的原理，但是还是可以给出一些直观的解释。我们知道，CNN越靠近输入端，其抽取的图像特征越原始。比如最初的一层通常只能抽取一些线条之类的元素。越上层，其特征越抽象。

而现实的图像无论多么复杂，总是由简单特征拼凑而成的。因此，无论最终的分类结果差异如何巨大，其底层的图像特征却几乎一致。

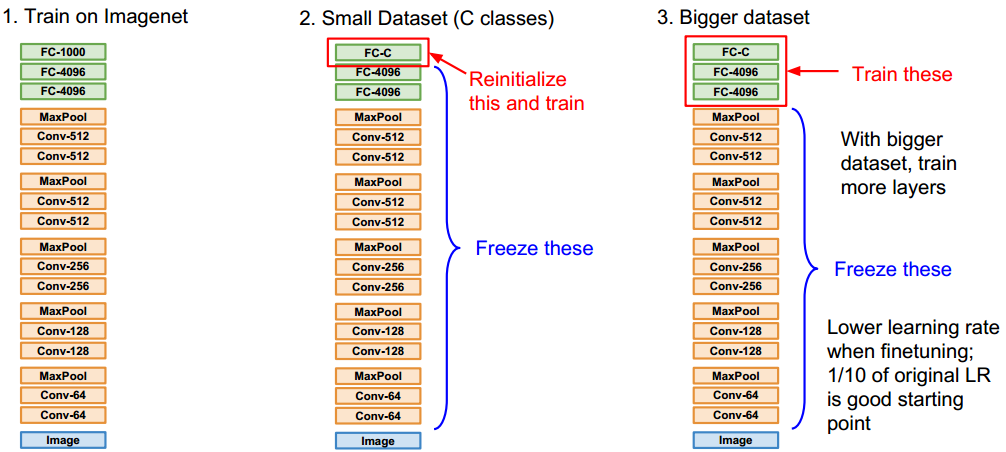
fine-tuning也是图像目标检测、语义分割的基础。

参考：

https://zhuanlan.zhihu.com/p/22624331

fine-tuning:利用已有模型训练其他数据集

http://www.cnblogs.com/louyihang-loves-baiyan/p/5038758.html

Caffe fine-tuning微调网络

http://blog.csdn.net/sinat_26917383/article/details/54999868

caffe中fine-tuning模型三重天（函数详解、框架简述）+微调技巧

h1ttps://www.zhihu.com/question/49534423

迁移学习与fine-tuning有什么区别？

https://zhuanlan.zhihu.com/p/37341493

基于Pre-trained模型加速模型学习的6点建议

https://mp.weixin.qq.com/s/54HQU3B4cSdRb1Z4srSfJg

如何为新类别重新训练一个图像分类器

Style Transfer

上图是Style Transfer问题的效果图：将图片B的风格迁移到另一张图片A上。

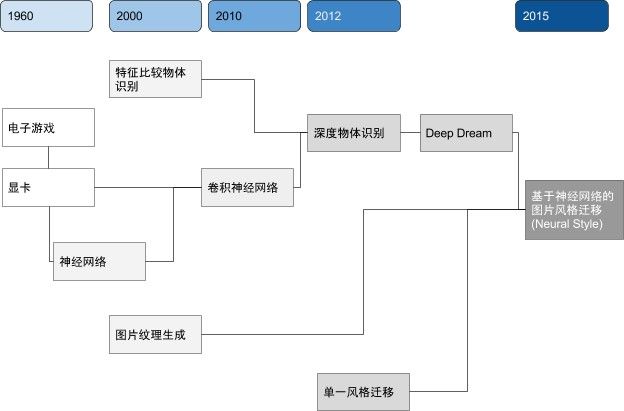
上图是图像风格迁移所涉及的科技树。

在继续讨论之前，我们有必要指出Style Transfer和其他传统的有监督学习的CV问题之间的差异。

1.风格这种抽象的概念，该如何定义？艺术领域的很多东西，通常都是很难量化的。如果要采用有监督学习的方法的话，怎么获得学习的标签呢？

2.就算解决了第1个问题，如何生成一批同一风格的图片也是一个大问题。画家可是稀缺资源啊。

因此，Style Transfer问题的关键点就在于：如何利用仅有的1张风格图片，将其风格迁移到其他图片上。

早期方法

图像风格迁移这个领域，在2015年之前，连个合适的名字都没有，因为每个风格的算法都是各管各的，互相之间并没有太多的共同之处。

比如油画风格迁移，里面用到了7种不同的步骤来描述和迁移油画的特征。又比如头像风格迁移里用到了三个步骤来把一种头像摄影风格迁移到另一种上。以上十个步骤里没一个重样的。

可以看出这时的图像风格处理的研究，基本都是各自为战，捣鼓出来的算法也没引起什么注意。

上图是一个油画风格迁移的pipe line。

在实践过程中，人们又发现图像的纹理可以在一定程度上代表图像的风格。下文如无特指，纹理/风格均为同义词。

这又引入了和风格迁移相关的另一个领域——纹理生成。这个时期，该领域虽然已经有了一些成果，但是通用性也比较差。

早期纹理生成的主要思想：纹理可以用图像局部特征的统计模型来描述。然而手工建模毕竟耗时耗力。。。