DL » 深度学习（八）——神经元激活函数进阶
2017-06-23 :: 6486 WordsLSTM（续）
https://mp.weixin.qq.com/s/jcS4IX7LKCt1E2FVzLWzDw
LSTM入门详解
https://mp.weixin.qq.com/s/MQR7c57NL4b5i4MRA2JgWA
用Python实现CNN长短期记忆网络！
http://mp.weixin.qq.com/s/V2-grLPdZ66FOiC2duc-EA
如何判断LSTM模型中的过拟合与欠拟合
http://blog.csdn.net/malefactor/article/details/51183989
深度学习计算模型中“门函数（Gating Function）”的作用
https://mp.weixin.qq.com/s/ORLpqqV8pOv-pIagi8yS1A
在调用API之前，你需要理解的LSTM工作原理
https://mp.weixin.qq.com/s/BzlFbweHEJ3z7dSIGmd-QA
深度学习基础之LSTM
https://mp.weixin.qq.com/s/lbHTDdzPbYn2Ln4aihGujQ
人人都能看懂的LSTM
https://mp.weixin.qq.com/s/LI6TsPjzIaa8DxDu3UaV1A
门控循环单元（GRU）的基本概念与原理
https://mp.weixin.qq.com/s/LcdmXgAFpiIoHMIIXECC9g
人人都能看懂的GRU
https://mp.weixin.qq.com/s/m_cOjUHwvW496Gv9_aYgpA
LSTM和循环神经网络基础教程
https://blog.csdn.net/taoqick/article/details/79475350
学会区分RNN的output和state
神经元激活函数进阶
在《深度学习（二）》中，我们探讨了ReLU相对于sigmoid函数的改进，以及一些保证深度神经网络能够训练的措施。然而即便如此，深度神经网络的训练仍然是一件非常困难的事情，还需要更多的技巧和方法。
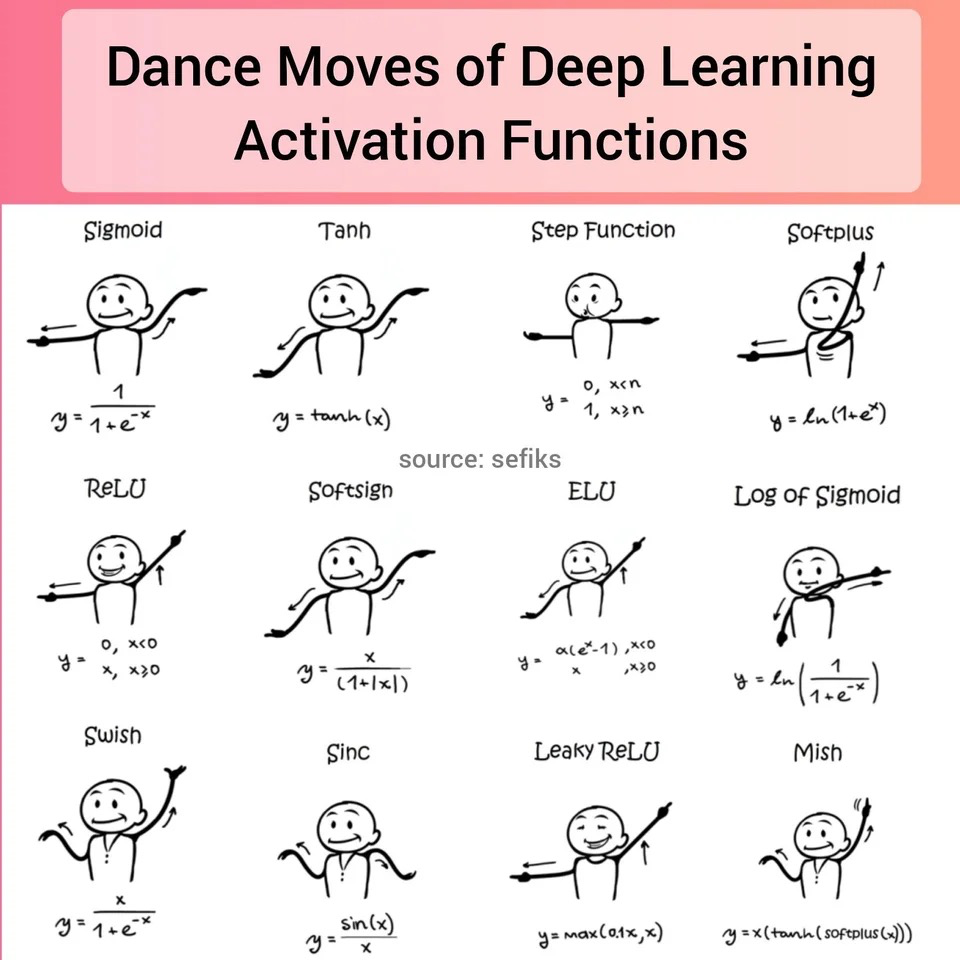
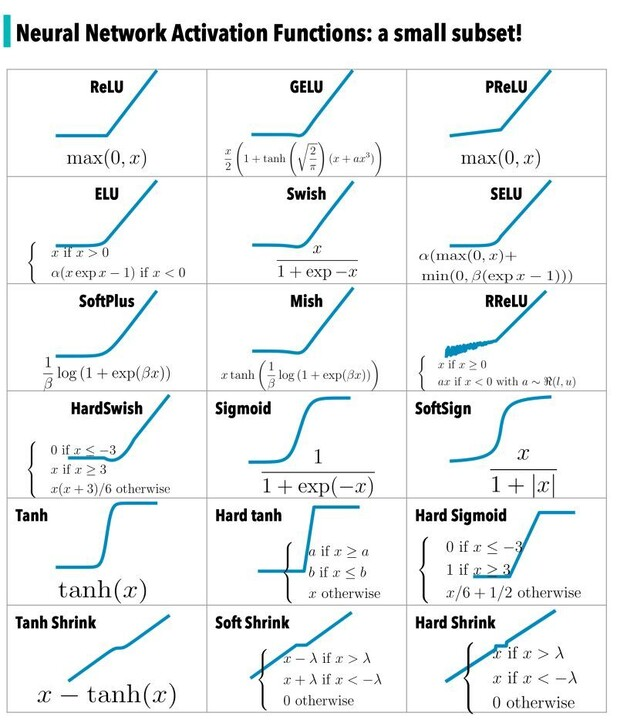
激活函数的作用
神经网络中激活函数的主要作用是提供网络的非线性建模能力，如不特别说明，激活函数一般而言是非线性函数。
假设一个神经网络中仅包含线性卷积和全连接运算，那么该网络仅能够表达线性映射，即便增加网络的深度也依旧还是线性映射，难以有效建模实际环境中非线性分布的数据。
加入非线性激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。因此，激活函数是深度神经网络中不可或缺的部分。
注意：其实也有采用线性激活函数的神经网络，亦被称为linear neurons。但是这些神经网络，基本只有学术价值而无实际意义。
理论上来说，只要是非线性函数，都有做激活函数的可能性。然而不同的激活函数其训练成本是不同的。
虽然OpenAI的探索表明，连浮点误差都可以做激活函数，但是由于这个操作的不可微分性，因此他们使用了“进化策略”来训练模型，所谓“进化策略”，是诸如遗传算法之类的耗时耗力的算法。
参考：
https://mp.weixin.qq.com/s/d9XmDCahK6UBlYWhI0D5jQ
深度线性神经网络也能做非线性计算，OpenAI使用进化策略新发现
https://mp.weixin.qq.com/s/PNe2aKVMYjV_Nd7qZwGuOw
理解激活函数作用，看这篇文章就够了！
ReLU的缺点
深度神经网络的训练问题，最早是2006年Hinton使用分层无监督预训练的方法解决的，然而该方法使用起来很不方便。
而深度网络的直接监督式训练的最终突破，最主要的原因是采用了新型激活函数ReLU。
但是ReLU并不完美。它在x<0时硬饱和，而当x>0时，导数为1。所以，ReLU能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。但随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为神经元死亡。
ReLU还经常被“诟病”的另一个问题是输出具有偏移现象，即输出均值恒大于零。偏移现象和神经元死亡会共同影响网络的收敛性。实验表明，如果不采用Batch Normalization，即使用MSRA初始化30层以上的ReLU网络，最终也难以收敛。
为了解决上述问题，人们提出了Leaky ReLU、PReLU、RReLU、ELU、Maxout等ReLU的变种。
Leaky ReLU:
\[f(x) = \begin{cases} x & \mbox{if } x > 0 \\ a x & \mbox{otherwise} \end{cases}\]这里的a是个常数，如果是个vector的话，那么就是PReLU了。
ELU：
\[f(x) = \begin{cases} x & \mbox{if } x \geq 0 \\ a(e^x-1) & \mbox{otherwise} \end{cases}\]Maxout
Maxout Networks是Ian J. Goodfellow于2013年提出的一大类激活函数。
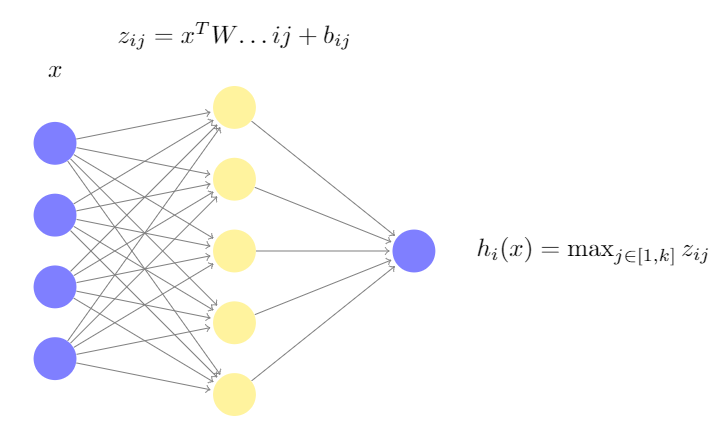
上图是Maxout Networks的结构图。传统的激活函数一般是这样的形式：\(\sigma(Wx+b)\)
Maxout Networks将\(Wx+b\)这部分运算，分成k个组。每组的w和b都不相同。然后对每组计算结果\(z_{ij}\)取最大值。
从这个意义来说，ReLU可以看做是Maxout的特殊情况，即：
\[y=\max(W_1x+b_1,W_2x+b_2)=\max(0,Wx+b)\]更多的情况参见下图：
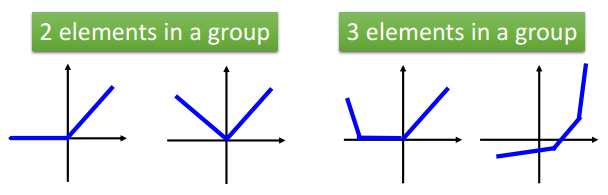
从Maxout Networks的角度来看，ReLU和DropOut实际上是非常类似的。
参考：
http://blog.csdn.net/hjimce/article/details/50414467
Maxout网络学习
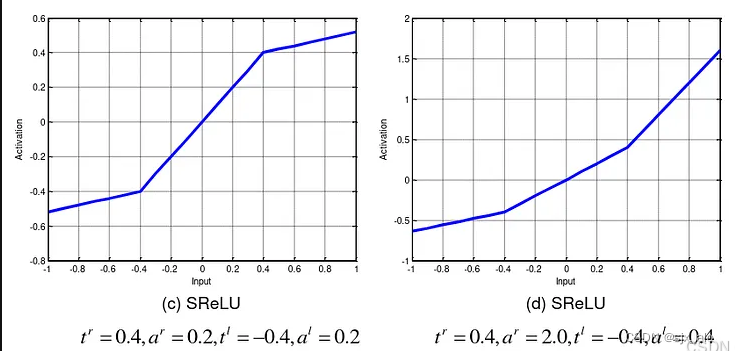
GLU
Gated Linear Unit是由facebook提出的：
\[(\boldsymbol{W}_1\boldsymbol{x}+\boldsymbol{b}_1)\otimes \sigma(\boldsymbol{W}_2\boldsymbol{x}+\boldsymbol{b}_2)\]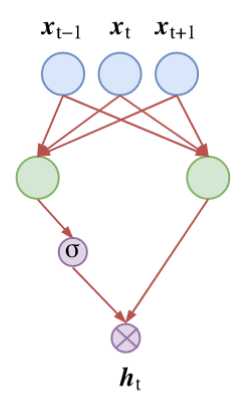
上图右侧是一个Linear Unit，左侧的\(\sigma\)相当于一个Gate，故名。
论文：
《Language Modeling with Gated Convolutional Networks》
GLU一般用在NLP领域，它和CNN结合，也就是所谓的GCNN了。
RRelu
论文：
《Empirical Evaluation of Rectified Activations in Convolution Network》
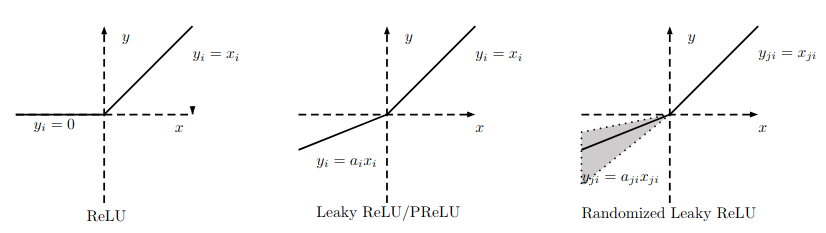
GELU
论文：
《Gaussian Error Linear Units (GELUs)》
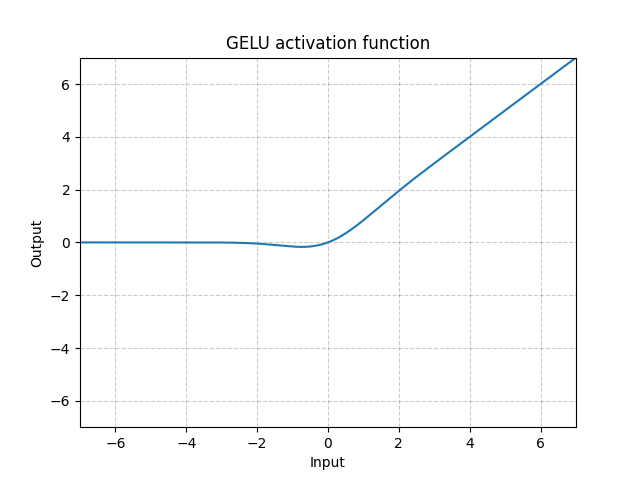
其中\(\Phi(x)\)是标准正态分布的累积概率函数，即：
\[\Phi(x)=\int_{-\infty}^x \frac{e^{-t^2/2}}{\sqrt{2\pi}}dt=\frac{1}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]\]上式中\(\text{erf}\)函数，也称为正态分布的误差函数。
\[erf(x)=\frac{2}{\sqrt{ \pi}}\int_0^{x}e^{-t^2}dt\]这个积分无法用初等函数表示，所以通常使用以下的近似泰勒展开式：
\[\text{GELU}(x)=x\Phi(x)\approx x\sigma(1.702 x)\] \[\text{GELU}(x)=x\Phi(x)\approx \frac{1}{2} x \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715 x^3\right)\right)\right]\]参考：
https://mp.weixin.qq.com/s/pA9JW75p9J5e5KHe3ifcBQ
从ReLU到GELU，一文概览神经网络的激活函数
https://mp.weixin.qq.com/s/LEPalstOc15CX6fuqMRJ8Q
超越ReLU却鲜为人知，3年后被挖掘：BERT、GPT-2等都在用的激活函数（GELU）
https://kexue.fm/archives/7309
GELU的两个初等函数近似是怎么来的
https://zhuanlan.zhihu.com/p/349492378
BERT中的激活函数GELU：高斯误差线性单元
https://www.cnblogs.com/htj10/p/8621771.html
正态分布（高斯分布）、Q函数、误差函数、互补误差函数
Swish
Swish是Google大脑团队提出的一个新的激活函数：
\[\text{Swish}(x, \beta)=x\cdot \text{sigmoid}(\beta x)\]其中，当\(\beta =1\)时，又被称为SiLU（Sigmoid Linear Unit）函数。
它的图像如下图中的橙色曲线所示：
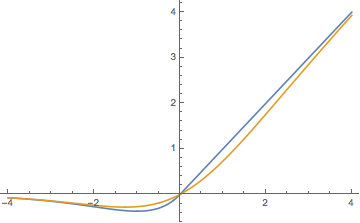
Swish可以看作是GLU的特例（Swish的两组参数相同）。
Swish在原点附近不是饱和的，只有负半轴远离原点区域才是饱和的，而ReLu在原点附近也有一半的空间是饱和的。
而我们在训练模型时，一般采用的初始化参数是均匀初始化或者正态分布初始化，不管是哪种初始化，其均值一般都是0，也就是说，初始化的参数有一半处于ReLu的饱和区域，这使得刚开始时就有一半的参数没有利用上。
特别是由于诸如BN之类的策略，输出都自动近似满足均值为0的正态分布，因此这些情况都有一半的参数位于ReLu的饱和区。
相比之下，Swish好一点，因为它在负半轴也有一定的不饱和区，所以参数的利用率更大。
苏剑林据此提出了自己的激活函数：
\[\max(x, x\cdot e^{-\mid x\mid })\]该函数的图像如上图的蓝色曲线所示。
参考：
https://mp.weixin.qq.com/s/JticD0itOWH7Aq7ye1yzvg
谷歌大脑提出新型激活函数Swish惹争议：可直接替换并优于ReLU？
http://kexue.fm/archives/4647/
浅谈神经网络中激活函数的设计
SwiGLU
SwiGLU是2019年提出的，它结合了SWISH和GLU两种者的特点。
\[\text{SwiGLU}(x,W,V,b,c)=\text{Swish}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})\otimes \sigma(\boldsymbol{V}\boldsymbol{x}+\boldsymbol{c})\]其他激活函数
hard tanh
\[\text{HardTanh}(x)=\begin{cases} -1, & x<-1 \\ x, & -1\le x \le 1 \\ 1, & x>1 \\ \end{cases}\]
hard tanh也叫做Relu1。
hard sigmoid
\[\text{HardSigmoid}(x)=\begin{cases} 0, & x<-2.5 \\ 0.2x, & -2.5\le x \le 2.5 \\ 1, & x>2.5 \\ \end{cases}\]
soft sign
\[\text{softsign}(x)=\frac{x}{1+\mid x\mid }\]Hardswish
\[Hardswish(x) = x\frac{RELU6(x+3)}{6} = \left\{ \begin{aligned} &0, & \text{if } x \leq -3 \\ &x, & \text{if } x \geq 3 \\ &\frac{x(x+3)}{6}, & \text{otherwise} \end{aligned} \right.\]Mish
\[Mish(x)=x\tanh (\ln(1+e^x))\]参考：
https://mp.weixin.qq.com/s/i8aShQvJhSgP7KY5Qgm36A
ReLU的继任者Mish：一个新的state of the art的激活函数
https://mp.weixin.qq.com/s/a_roXfjNX2szJMUrww0Fmg
YOLOv4中的Mish激活函数
soft relu
\[soft\_ relu(x) = \ln(1 + \exp(\max(\min(x, threshold), -threshold)))\]SELU
CELU
CRELU
\[CReLU(x)= Concat[ ReLU(x), ReLU(−x) ]\]参考
https://zhuanlan.zhihu.com/p/22142013
深度学习中的激活函数导引
http://blog.csdn.net/u012328159/article/details/69898137
几种常见的激活函数
https://mp.weixin.qq.com/s/Hic01RxwWT_YwnErsJaipQ
什么是激活函数？
https://mp.weixin.qq.com/s/4gElB_8AveWuDVjtLw5JUA
深度学习激活函数大全
https://mp.weixin.qq.com/s/7DgiXCNBS5vb07WIKTFYRQ
从ReLU到Sinc，26种神经网络激活函数可视化
http://www.cnblogs.com/ymjyqsx/p/6294021.html
PReLU与ReLU
http://www.cnblogs.com/pinard/p/6437495.html
深度神经网络（DNN）损失函数和激活函数的选择
https://mp.weixin.qq.com/s/VSRtjIH1tvAVhGAByEH0bg
21种NLP任务激活函数大比拼：你一定猜不到谁赢了
https://www.cnblogs.com/makefile/p/activation-function.html
激活函数(ReLU, Swish, Maxout)
您的打赏，是对我的鼓励
