DL » 深度学习（五）——AutoEncoder, 词向量（1）
2017-06-15 :: 5782 WordsCNN（续）
参考
http://blog.csdn.net/Fate_fjh/article/details/52882134
卷积神经网络系列blog
https://zhuanlan.zhihu.com/p/47184529
卷积神经网络（CNN）详解
http://mp.weixin.qq.com/s/YRwGwelyA3VOYZ4XGAjUBw
CNN感受野首次可视化：深入解读及计算指南
https://mp.weixin.qq.com/s/EJyG3Y4EHTGMm_Q1mY4RvA
CNN入门手册（上）
https://mp.weixin.qq.com/s/T3tHFdjnQh4asE0V25vTog
CNN入门手册（中）
https://mp.weixin.qq.com/s/chsDjS39qcoHICUNbSdQHQ
长文揭秘图像处理和卷积神经网络架构
https://mp.weixin.qq.com/s/nIbfiDXkqkpdLzQo2Gmc2Q
利用卷积神经网络处理CIFAR图像分类
https://mp.weixin.qq.com/s/5BMU7SRQeuDg68XDcOUBZw
训练集样本不平衡问题对CNN的影响
https://mp.weixin.qq.com/s/p-wZ_6ZQW-zXzDqmRenNow
深度学习入门：几幅手稿讲解CNN
https://mp.weixin.qq.com/s/xXf7hTfH-vx4YbzlZVQucA
CNN入门再介绍
https://mp.weixin.qq.com/s/Q4snAlAi8tPQAyGm0qUy4w
CNN的全面解析
https://mp.weixin.qq.com/s/Do6erhin3W4dK_-RTAyD6A
卷积神经网络(CNN)概念解释
http://www.qingruanit.net/blog/23930/note5837.html
卷积神经网络（CNN）学习算法之—基于LeNet网络的中文验证码识别
https://mp.weixin.qq.com/s/XiaAPd20YxbM0wDiSTAYMg
深度学习之卷积神经网络(CNN)的模型结构
https://mp.weixin.qq.com/s/x-H6h4sRqTrZlOXKStnhPw
卷积神经网络背后的数学原理
https://mp.weixin.qq.com/s/qIdjHqurqvdahEd0dXYIqA
徒手实现CNN：综述论文详解卷积网络的数学本质
https://mp.weixin.qq.com/s/D6ok6dQqyx6cCJKc2M8YpA
从AlexNet剖析-卷积网络CNN的一般结构
https://mp.weixin.qq.com/s/XZeZX8zTtNom0az_ralp4A
ImageNet冠军带你入门计算机视觉：卷积神经网络
https://mp.weixin.qq.com/s/t8jg_bpEcQiJmgIqKarefQ
卷积神经网络CNN学习笔记
https://mp.weixin.qq.com/s/buRuerMHkRMSSVlvmlDdtw
人人都能读懂卷积神经网络：Convolutional Networks for everyone
https://mp.weixin.qq.com/s/3pIybS_GsuN6XobP_4bLrg
深度学习以及卷积基础
https://mp.weixin.qq.com/s/VcjivPhJuCk7NPQ1FNQULw
一文让你入门CNN
https://mp.weixin.qq.com/s/zvPNuP_LT7pWIgoxzfeUWw
综述卷积神经网络：从基础技术到研究前景
AutoEncoder
Basic AE
Bengio在2003年的《A neural probabilistic language model》中指出，维度过高，会导致每次学习，都会强制改变大部分参数。
由此发生蝴蝶效应，本来很好的参数，可能就因为一个小小传播误差，就改的乱七八糟。
因此，数据降维是数据预处理中，非常重要的一环。常用的降维算法，除了线性的PCA算法之外，还有非线性的Autoencoder。
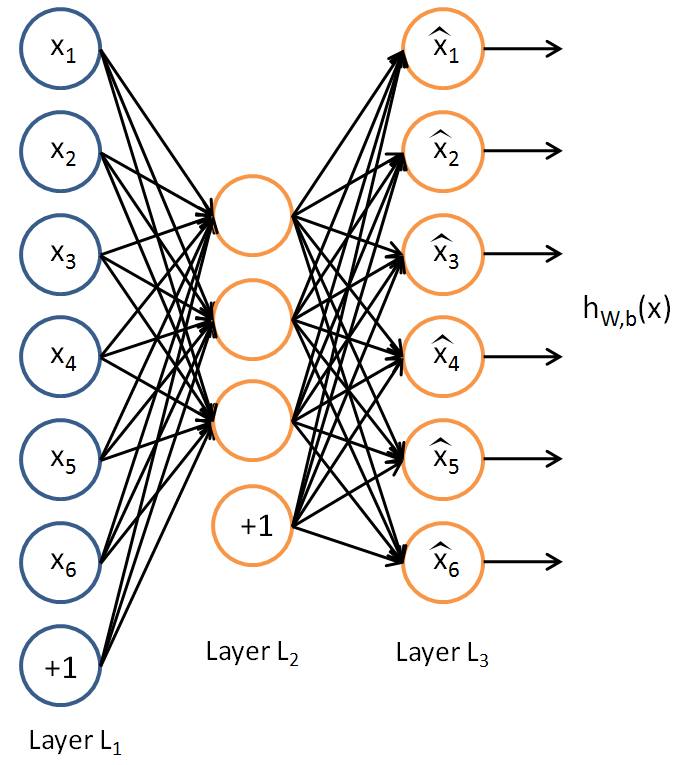
Autoencoder的结构如上图所示。它的特殊之处在于：
1.输入样本就是输出样本。
2.隐藏层的神经元数量小于样本的维度。
粗看起来，这类恒等变换没有太大意义。然而这类恒等变换之所以能够成立，最根本的地方在于，隐藏层的神经元具有表达输出样本的能力，也就是用低维表达高维的能力。反过来，我们就可以利用这一点，实现数据的降维操作。
但是，不是所有的数据都能够降维，而这种情况通常会导致Autoencoder的训练失败。
类似的，如果隐藏层的神经元数量大于样本的维度，则该AE可用于升维。这样的AE又叫做Sparse autoencoders。
总体来看，AE是个Encoder/Decoder结构。我们上面提到的降维/升维，主要是利用了Encoder部分。而Decoder部分也是很有意义的，它表明我们能够从tensor生成样本，这实际上就是一种生成模型。
和Autoencoder类似的神经网络还有：Denoising Autoencoder（DAE）。
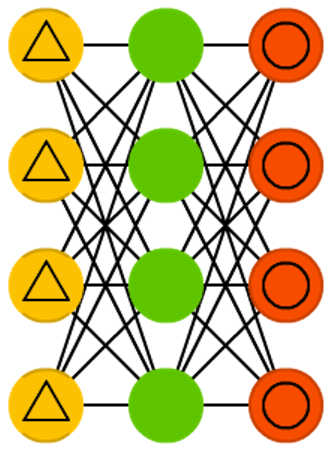
黄色的三角表明输入数据中被加入了噪声。当然了DAE的输出要和无噪声样本做比较，这样才能体现去噪的效果。
Stacked AutoEncoders
AE不仅可以单独使用，还可以堆叠式的使用。
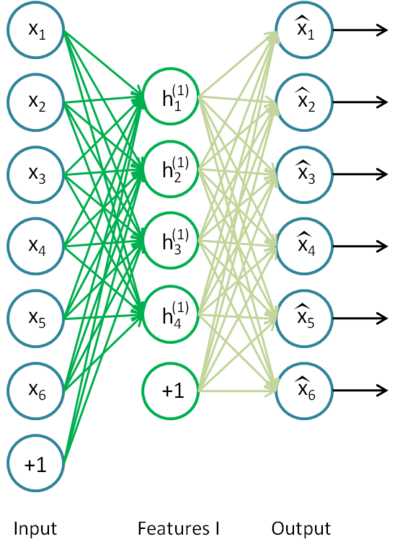
上图是个普通的AE，其中的hidden层可以看作是input的Features，不妨称作Features I。
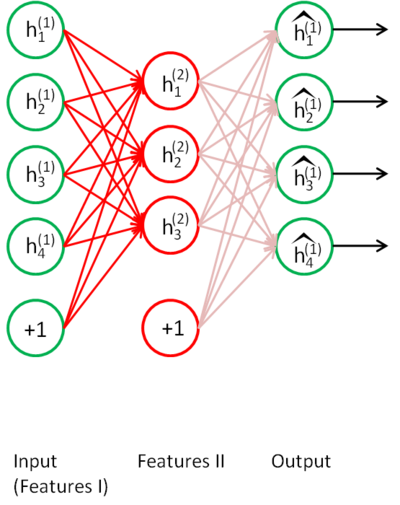
将Features I作为input，送进另一个AE，得到Features II。依此类推，就可以形成一个深度网络，这种方法叫做Stacked Auto-encoder Networks（SANs）。
这实际上，就是Relu发明之前，预训练DNN的标准做法。经过SANs预训练的网络，每层的参数都被归一化，即使使用sigmoid激活函数，也没有严重的梯度消失现象，从而使DNN的训练成为了可能。
参考：
http://ufldl.stanford.edu/wiki/index.php/Stacked_Autoencoders
Stacked Autoencoders
Deep AE
一层的AE有时可能不能很好的进行数据降维，这个时候就可以使用如下所示的Deep AE：
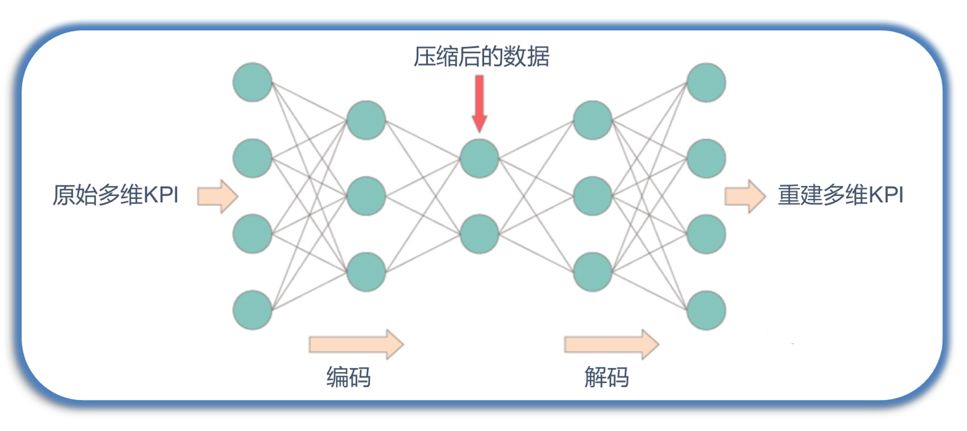
Deep AE可用于异常检测：根据正常数据训练出来的Autoencoder，能够将正常样本重建还原，但是却无法将异于正常分布的数据点较好地还原，导致还原误差较大。
参考：
http://sofasofa.io/tutorials/anomaly_detection/
利用Autoencoder进行无监督异常检测
https://zhuanlan.zhihu.com/p/51053142
基于自编码器的时间序列异常检测算法
https://mp.weixin.qq.com/s/Jqsm_JxI28SVXFt3Xuw8ew
使用自编码器进行图像去噪
参考
http://ufldl.stanford.edu/tutorial/unsupervised/Autoencoders/
Autoencoders
http://blog.csdn.net/changyuanchn/article/details/15681853
深度学习之autoencoder
https://mp.weixin.qq.com/s/cago4myCcLZkv1e43T__3g
深入理解自编码器
http://www.cnblogs.com/neopenx/p/4370350.html
降噪自动编码器（Denoising Autoencoder)
https://mp.weixin.qq.com/s/lODy8ucB3Bw9Y1sy1NxTJg
无监督学习中的两个非概率模型：稀疏编码与自编码器
https://mp.weixin.qq.com/s/QuDa__mi1NX1wOxo5Ki94A
深度学习：自动编码器基础和类型
http://blog.csdn.net/losteng/article/details/51067216
CAE(Convolutional Auto-Encode) 卷积自编码
https://mp.weixin.qq.com/s/q-WExyS-zylMA-L8ojOgRg
简单易懂的自动编码器
https://mp.weixin.qq.com/s/Ci0HPy3ENz1ZooB784aMcA
谷歌大脑Wasserstein自编码器：新一代生成模型算法
https://mp.weixin.qq.com/s/Pgf6JMokilV9JxYWi7Y20Q
揭秘自编码器，一种捕捉数据最重要特征的神经网络
https://mp.weixin.qq.com/s/FpPlSMfbtcxg_UnH0lwaqA
手把手教你实现去噪自编码器（Denoise Autoencoder）
https://zhuanlan.zhihu.com/p/82415579
浅谈Deep Auto-encoder
https://mp.weixin.qq.com/s/PJ-FiDQ7zYN_9rFVWkpeQA
降维算法：主成分分析 VS 自动编码器
词向量
One-hot Representation
NLP是ML和DL的重要研究领域。但是多数的ML或DL算法都是针对数值进行计算的，因此如何将自然语言中的文本表示为数值，就成为了一个重要的基础问题。
词向量顾名思义就是单词的向量化表示。最简单的词向量表示法当属One-hot Representation：
假设语料库的单词表中有N个单词，则词向量可表示为N维向量\([0,\dots,0,1,0,\dots,0]\)
这种表示法由于N维向量中只有一个非零元素，故名。该非零元素的序号，就是所表示的单词在单词表中的序号。
某牛点评：
如果你预测的label是苹果，雪梨，香蕉，草莓这四个，显然他们不直接构成比较关系，但如果我们用1,2,3,4来做label就会出现了比较关系，label之间的距离也不同。有了比较关系，第一个label和最后一个label的距离太远，影响模型的学习。因为模型觉得label 1和label 2最像，和最后一个label最不像。
不过当你的label之间存在直接的比较关系，就可以直接用数字当label。例如你做一个风控模型，预测的是四个风险类别[低，中，高，紧急]，其实你也可以用1，2，3，4来做label，因为确实存在一个比较。但这本质上就成了回归问题。
One-hot Representation的缺点在于：
1.该表示法中，由于任意两个单词的词向量都是正交的，因此无法反映单词之间的语义相似度。
2.一个词库的大小是\(10^5\)以上的量级。维度过高，会妨碍神经网络学习到稀疏特征。
参考：
https://mp.weixin.qq.com/s?__biz=MzI4MzM2NTU0Mg==&mid=2247483698&idx=1&sn=cf185232e43b4523ab9b0bc0ce425ed4
One-Hot编码与哑变量
https://www.zhihu.com/question/359742335
分类问题的label为啥必须是one hot形式？
https://mp.weixin.qq.com/s/gDqI3ttGiZaeOzm7Gvc9dA
数据处理：离散型变量编码及效果分析
https://mp.weixin.qq.com/s/eRxvx1a03p-1nzatJGYQhQ
为什么独热编码会引起维度诅咒以及避免他的几个办法
Word Embedding
针对One-hot Representation的不足，Bengio提出了Distributed Representation，也称为Word Embedding。
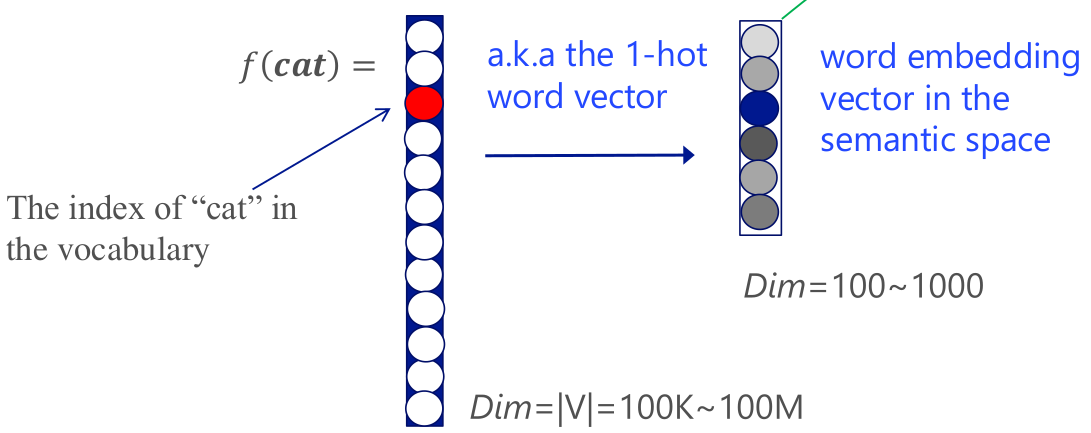
Word Embedding的思路如上图所示，即想办法将高维的One-hot词向量映射到低维的语义空间中。
Bengio自己提出了一种基于神经网络的Word Embedding的方案，然而由于计算量过大，目前已经被淘汰了。
参考：
http://www.cnblogs.com/neopenx/p/4570648.html
词向量概况
word2vec
除了Bengio方案之外，早期人们还尝试过基于共生矩阵（Co-occurrence Matrix）SVD分解的Word Embedding方案。该方案对于少量语料有不错的效果，但一旦语料增大，计算量即呈指数级上升。
这类方案的典型是Latent Semantic Analysis(LSA)。参见《机器学习（二十一）》。
Tomas Mikolov于2013年对Bengio方案进行了简化改进，提出了目前最为常用的word2vec方案。
介绍word2vec的数学原理比较好的有：
《Deep Learning实战之word2vec》，网易有道的邓澍军、陆光明、夏龙著。
《word2vec中的数学》，peghoty著。该书的网页版：
http://blog.csdn.net/itplus/article/details/37969519
这里有一个图解版本：
https://jalammar.github.io/illustrated-word2vec/
以及它的中文译本：
https://mp.weixin.qq.com/s/cpzBBntlFw6BDNUs6emCWw
详细图解Word2vec
老惯例这里只对最重要的内容进行摘要。
您的打赏，是对我的鼓励
