DL » 深度学习(四)——Neural Network Zoo, CNN
2017-06-14 :: 5238 Words深度学习常用术语解释
Batch Normalization(续)
参考:
http://blog.csdn.net/malefactor/article/details/51476961
Batch Normalization导读
http://www.cnblogs.com/neopenx/p/5211969.html
从Bayesian角度浅析Batch Normalization
http://blog.csdn.net/hjimce/article/details/50866313
Batch Normalization学习笔记
https://buptldy.github.io/2016/08/18/2016-08-18-Batch_Normalization/
Implementation of Batch Normalization Layer(中文blog)
https://www.zhihu.com/question/38102762
深度学习中 Batch Normalization为什么效果好?
https://mp.weixin.qq.com/s/OAn8y_uJTgyrtS2ZCyudlg
Batch Normalization原理及其TensorFlow实现
http://blog.csdn.net/u013709270/article/details/70949304
深度神经网络训练的必知技巧
https://mp.weixin.qq.com/s/Oy2GIZLbQxmXMCLzMapWHQ
Batch Normalization的分析与展望
https://www.jianshu.com/p/35a3bf866c46
浅析数据标准化和归一化,优化机器学习算法输出结果
https://blog.csdn.net/u010315668/article/details/80374711
机器学习之特征归一化(normalization)
https://www.jianshu.com/p/95a8f035c86c
归一化(Normalization)、标准化(Standardization)和中心化/零均值化(Zero-centered)
https://mp.weixin.qq.com/s/gWcejm_CMGPKes6tUhbQ5A
BatchNorm的避坑指南
深度学习常用术语解释
鞍点
在微分方程中,沿着某一方向是稳定的,而另一方向是不稳定的奇点,叫做鞍点(Saddle point)。在泛函中,既不是极大值点也不是极小值点的临界点,叫做鞍点。在矩阵中,一个数在所在行中是最大值,而在所在列中是最小值,则被称为鞍点。在物理上要广泛一些,指在一个方向是极大值,另一个方向是极小值的点。
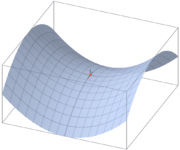
上图是\(z=x^2-y^2\)的曲面图,其中的原点就是鞍点。上图形似马鞍,故名。
长期以来,人们一直认为非凸优化的难点在于容易陷入局部最小,例如下图所示的Ackley函数。
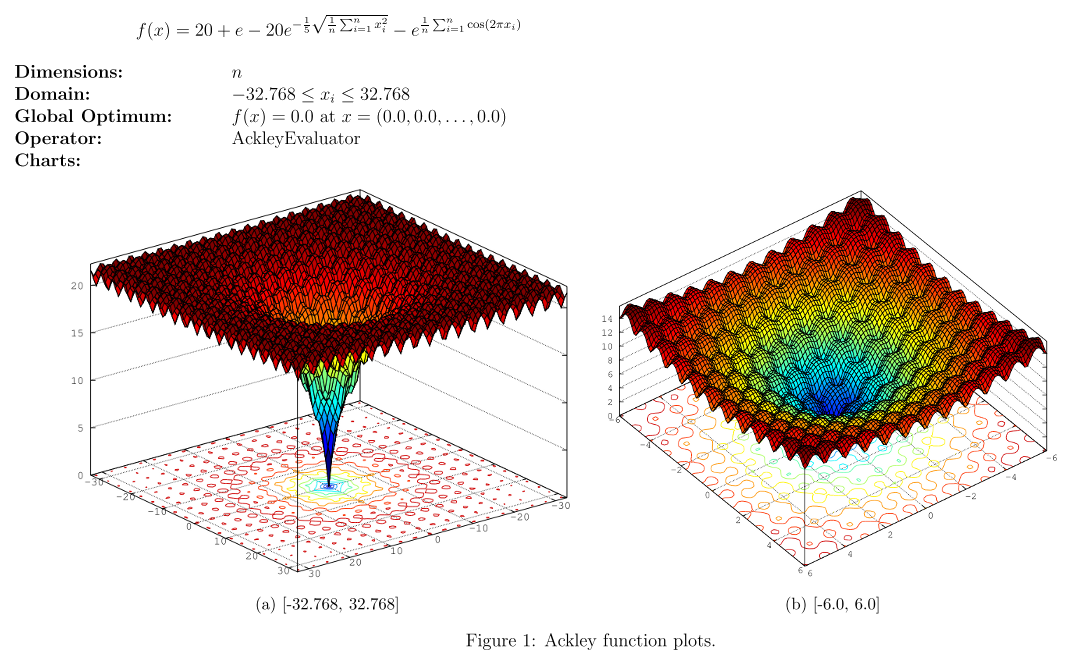
然而,LeCun和Bengio的研究表明,在high-D(高维)的情况下,局部最小会随着维度的增加,指数型的减少,在深度学习中,一个点是局部最小的概率非常小,同时鞍点无处不在。
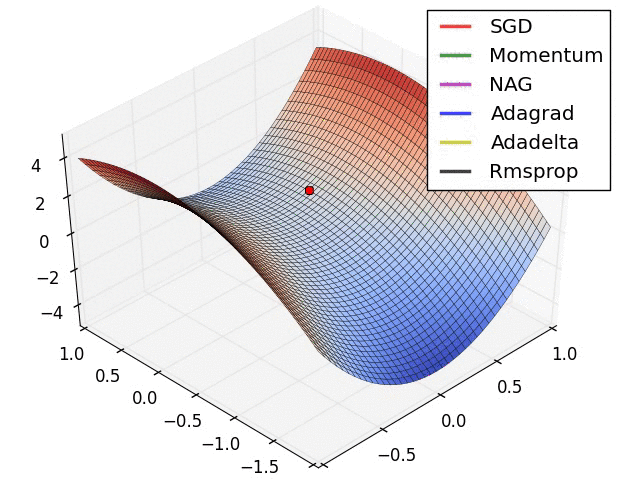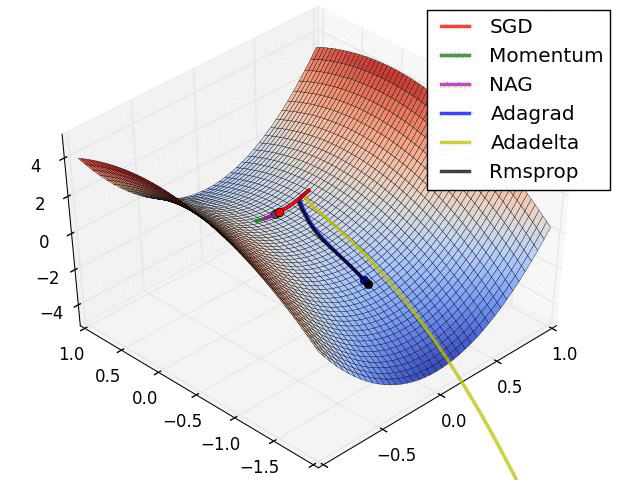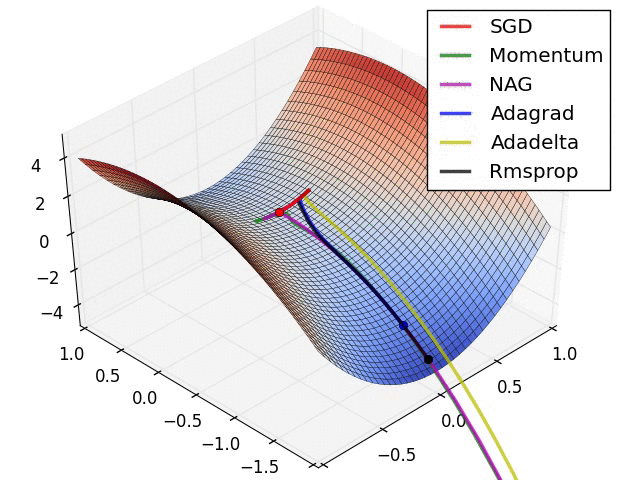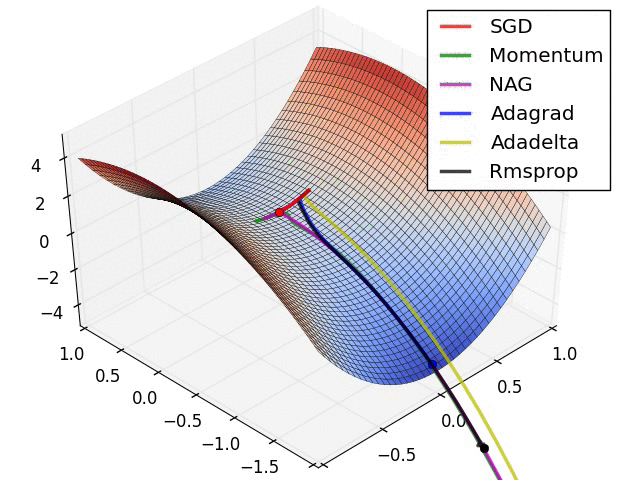
这是各种优化方法逃离鞍点的动画。
参考:
https://mp.weixin.qq.com/s/Cava8C_s4JikR0BTHx__KQ
神经网络逃离鞍点
欠拟合和过拟合
在DL领域,欠拟合意味着神经网络没有学到该学习的特征,而过拟合则意味着神经网络学习到了不该学习的特征。
在之前的描述中,我们一直强调过拟合的风险,然而实际上,欠拟合才是DL最大的敌人。
过拟合至少在训练集上表现出色,可以想象如果预测样本恰好和训练集样本近似的话,则模型是能够正确预测的。而欠拟合基本什么也做不了。
比如下面的场景:
1.对同一训练样本集\(T_1\),进行两次训练,分别得到模型\(M_1,M_2\)。
2.使用\(M_1,M_2\)对同一测试样本集\(T_2\)进行预测,得到预测结果集\(P_1,P_2\)。
3.如果\(P_1,P_2\)的结论基本相反的话,则说明发生了欠拟合现象。而过拟合则并没有这么夸张的效果。
参考:
https://mp.weixin.qq.com/s/zv8Mtch5Klm-qSgyBxI9QQ
六步走,时刻小心过拟合
https://zhuanlan.zhihu.com/p/74553341
过参数化、剪枝和网络结构搜索
模型容量
如果你切换到工业级数据集,上亿条数据的时候,你会发现有些模型会随着数据量的增大,效果持续变好,而其他模型,一开始随着数据增加上升很快,但慢慢就会进入一个瓶颈期,再怎么增加数据都无法提高了。我们一般认为这是模型容量导致的。
Neural Network Zoo
在继续后续讲解之前,我们首先给出常见神经网络的结构图:
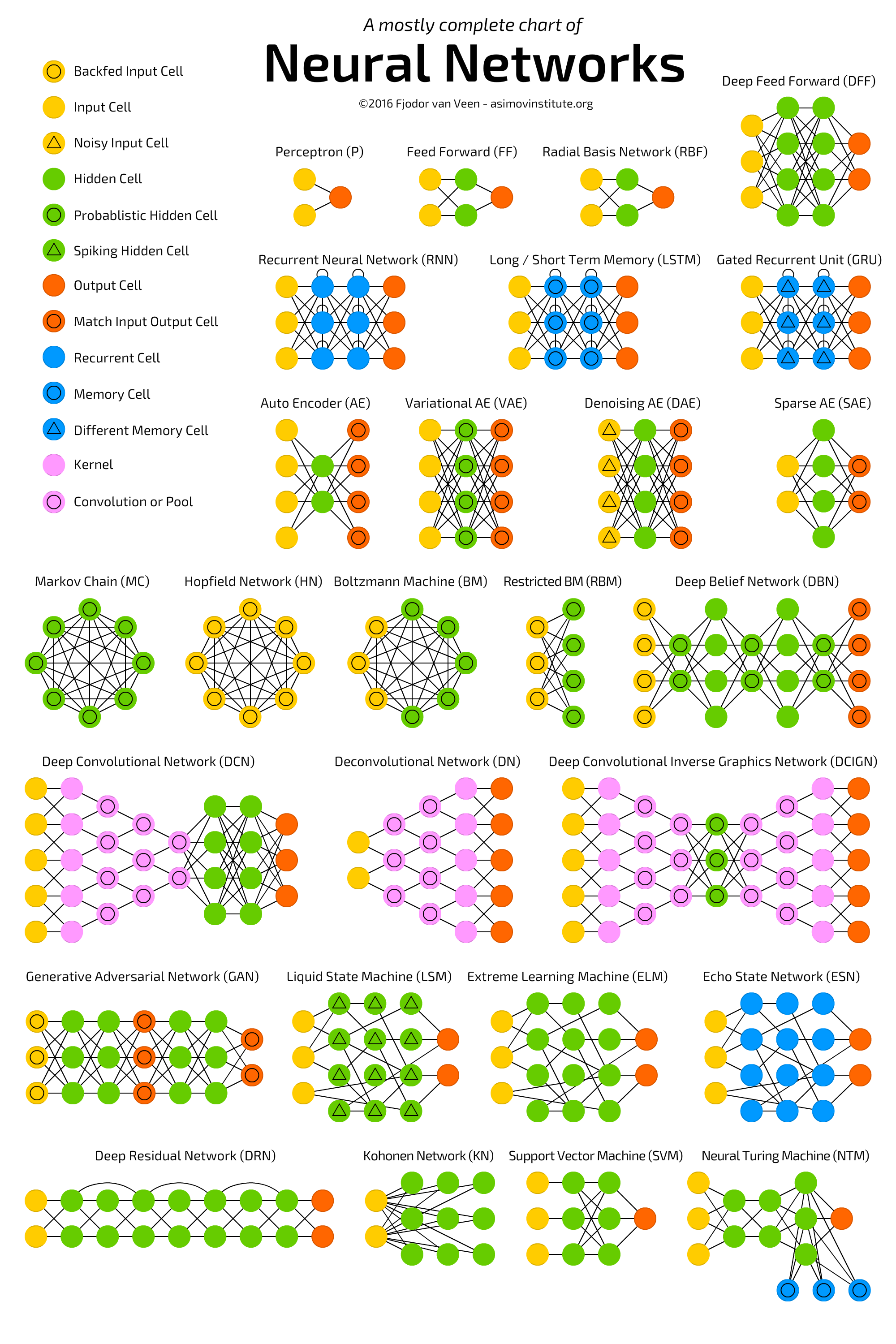
上图的原地址为:
http://www.asimovinstitute.org/neural-network-zoo/
单元结构:

层结构:
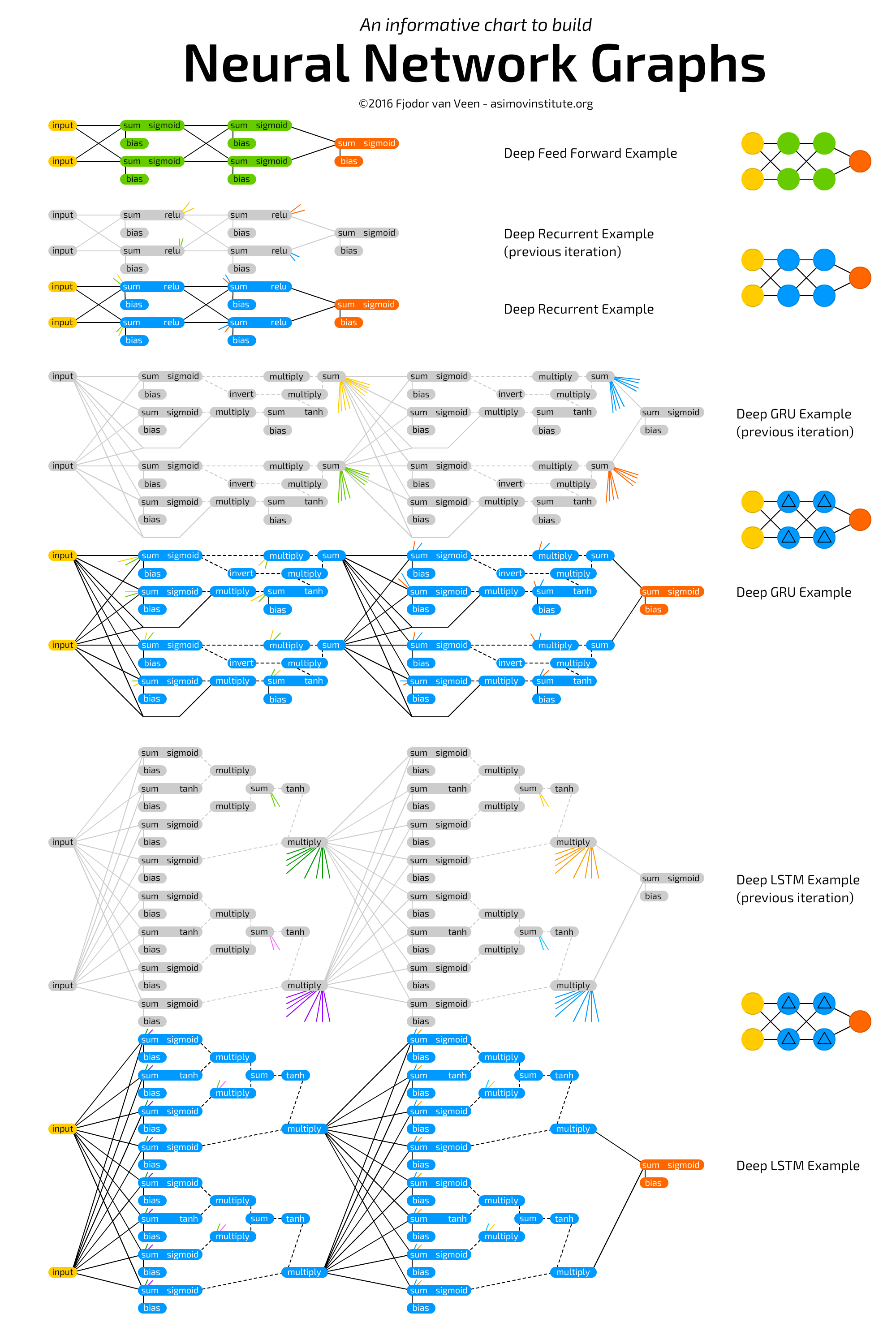
上图的原地址为:
http://www.asimovinstitute.org/neural-network-zoo-prequel-cells-layers/
参考:
https://mp.weixin.qq.com/s/ysnLwvbSD4fcL5LK7wSnyA
MIT高赞深度学习教程:一文看懂CNN、RNN等7种范例
CNN
概述
卷积神经网络(Convolutional Neural Networks,ConvNets或CNNs)属于神经网络的范畴,已经在诸如图像识别和分类的领域证明了其高效的能力。
CNN的开山之作是Yann LeCun的论文:
《Gradient-Based Learning Applied to Document Recognition》
科学界的许多重要成果的开山之作,其名称往往和成果的最终名称有一定的差距。比如LeCun的这篇文章的名称中,就没有CNN。类似的还有Vapnik的SVM,最早被称为Support Vector Network。
英文不好的,推荐以下文章:
http://www.hackcv.com/index.php/archives/104/
CNN的直观解释
https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/
上面文章的英文版本
关键点
这里以最经典的LeNet-5为例,提点一下CNN的要点。
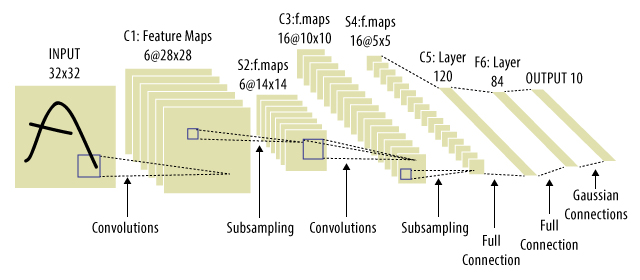
LeNet-5的caffe模板:
https://github.com/BVLC/caffe/blob/master/examples/mnist/lenet.prototxt
卷积
在《数学狂想曲(十六)》中我们讨论了卷积的数学含义,结合《 图像处理理论(一)》和《 图像处理理论(二)》,不难看出卷积或者模板(算子, kernel, filter),在前DL时代,几乎是图像处理算法的基础和灵魂。
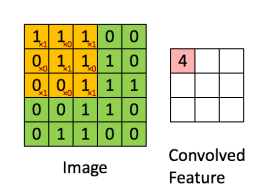
为了实现各种目的,人们手工定义或发现了一系列算子:

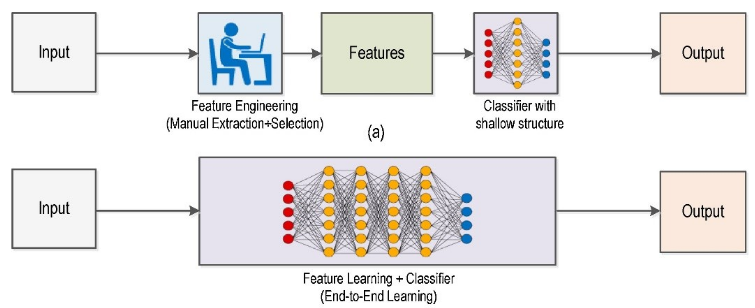
到了DL时代,卷积仍然起着非常重要的作用。但这个时候,不再需要人工指定算子,算子本身也将由学习获得。我们需要做的只不过是指定算子的个数而已。


上面的两图形象的指出了ML和DL的差别。
比如,LeNet-5的C1:6@28*28,其中的6就是算子的个数。显然算子的个数越多,计算越慢。但太少的话,又会导致提取的特征数太少,神经网络学不到东西。
需要注意的是,传统的CV算法中,通常只有单一的卷积运算。而CNN中的卷积层,实际上包括了卷积+激活两种运算,即:
\[L_2=\sigma(Conv(L_1,W)+b)\]因此,相比全连接层而言,卷积层每次只有部分元素参与到最终的激活运算。从宏观角度看,这些元素实际上对应了图片的局部空间二维信息,它和后面的Pooling操作一道,起到了空间降维的作用。
实际上,传统的MLP(MultiLayer Perceptron)网络,就是由于1D全连接的神经元控制了太多参数,而不利于学习到稀疏特征。
CNN网络中,2D全连接的神经元则控制了局部感受野,有利于解离出稀疏特征。
至于激活函数,则是为了保证变换的非线性。这也是CNN被归类为NN的根本原因。
参考:
https://mp.weixin.qq.com/s/dIIWAKv9woLO8M0CyN8lsw
传统计算机视觉技术落伍了吗?不,它们是深度学习的“新动能”
池化
Pooling操作(也称Subsampling)使输入表示(特征维度)变得更小,并且网络中的参数和计算的数量更加可控的减小,因此,可以控制过拟合。
它还可使网络对于输入图像中更小的变化、冗余和变换变得不变性。
Gaussian Connections
LeNet-5最后一步的Gaussian Connections是一个当年的历史遗迹,目前已经被Softmax所取代。它的含义在上面提到的Yann LeCun的原始论文中有描述。
注意:现代版的LeNet-5最后一步的Softmax层,实际上包含了\(Wx+b\)和Softmax两种计算。相当于用Softmax函数替换Sigmoid/ReLU函数。
其他
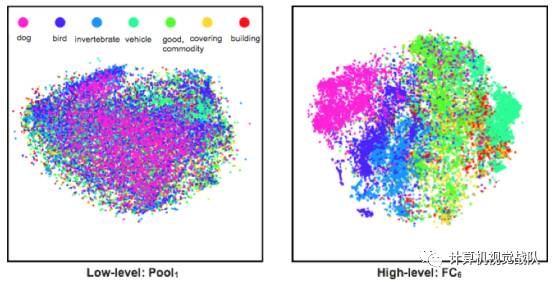
上图展示了不同分类的图片特征在特征空间中的分布,可以看出在CNN的低层中,这些特征是混杂在一起的;而到了CNN的高层,这些特征就被区分开来了。
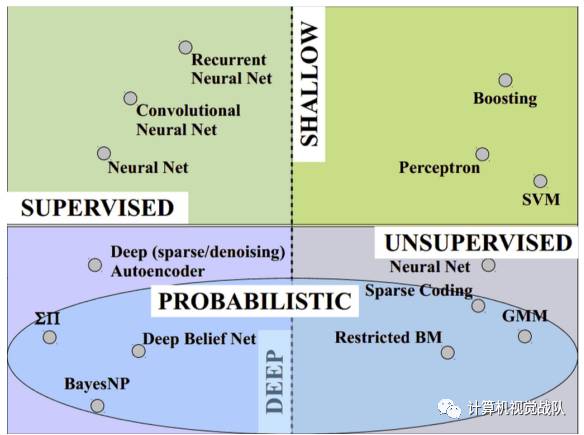
上图是若干ML、DL算法按照不同维度划分的情况。
多通道卷积
MNIST的例子中,由于图像是单通道(灰度图)的,因此,多数教程都只是展示了单通道卷积的计算步骤:
\[g(i,j)=\sum_{k,l}f(i+k,j+l)h(k,l)\]而多通道(例如彩色图像的RGB三通道)卷积实际上就是将各通道卷积之后的结果再加在一起:
\[g(i,j)=\sum_{c,k,l}f(i+k,j+l)h(k,l)\]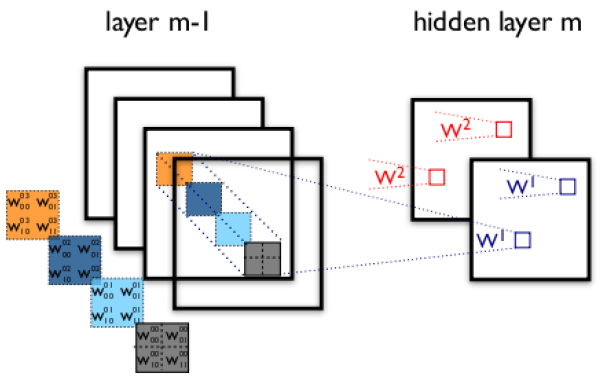
上图展示了一个4通道图像经卷积之后,得到2通道图像的过程。
从中可以得出以下结论:
1.RGB通道信息在卷积之后,就不复存在了。无论输入图像有多少个通道,输出图像的通道数只和feature的个数相关。
2.即使是LeNet-5的MNIST示例中,实际上也是有多通道卷积的,只不过不在第一个卷积层而已。
3.多通道卷积除了二维空间信息的卷积之外,还包括了通道间信息的卷积。这也是CNN中1x1卷积的意义之一。
CNN的反向传播算法
由于卷积和池化两层,不是一般的神经网络结构。因此CNN的反向传播算法实际上也是很有技巧的。
上面提到卷积操作可以转换为矩阵运算:\(y=Cx\)
其对应的梯度反向传播公式为:
\[\frac{\partial Loss}{\partial x} = \frac{\partial y^T}{\partial x}\cdot \frac{\partial Loss}{\partial y} = C^T \cdot \frac{\partial Loss}{\partial y}\]因此:
正向:\(Y=X*K\)
反向:\(\Delta X = \Delta Y * rot_{180}(K)\)
ConvBackpropInput:
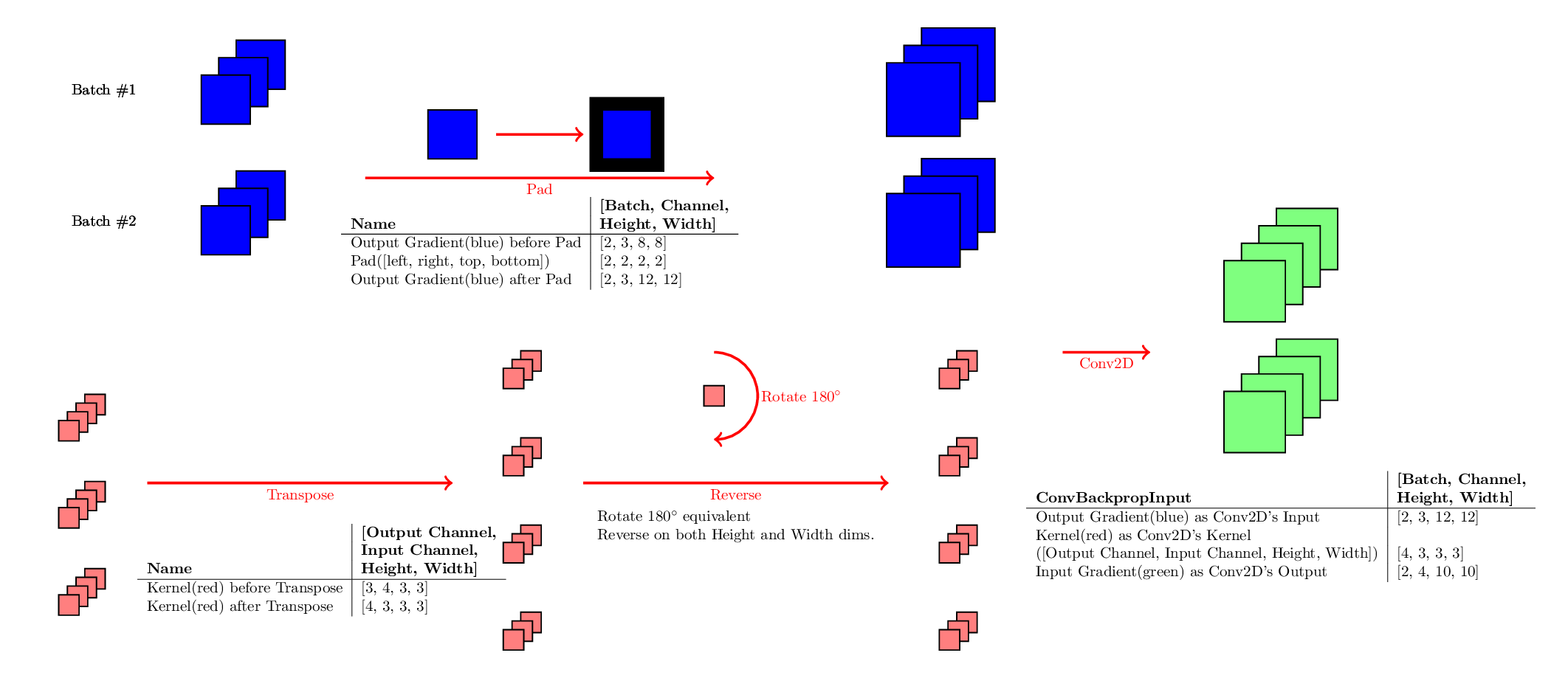
ConvBackpropFilter:
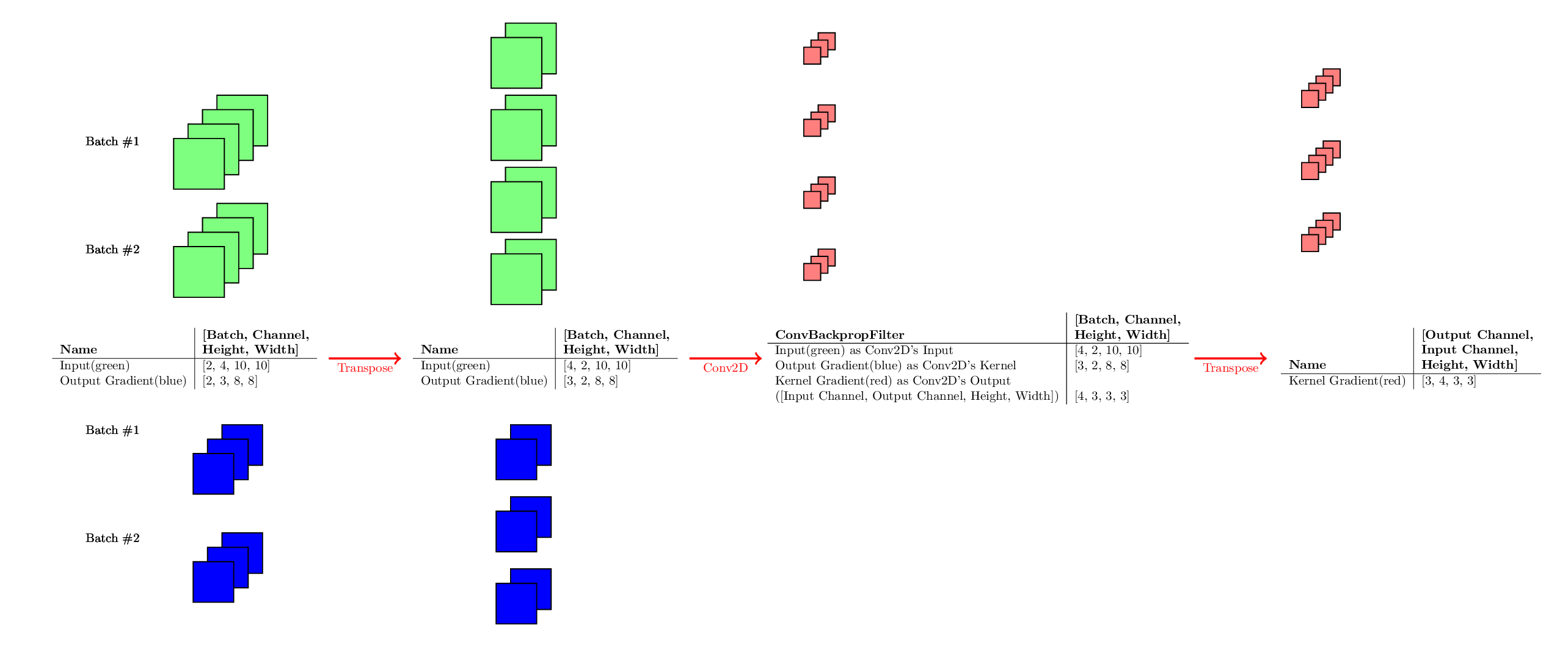
卷积的反向传播,有时也被称为反卷积(Deconvolution)。
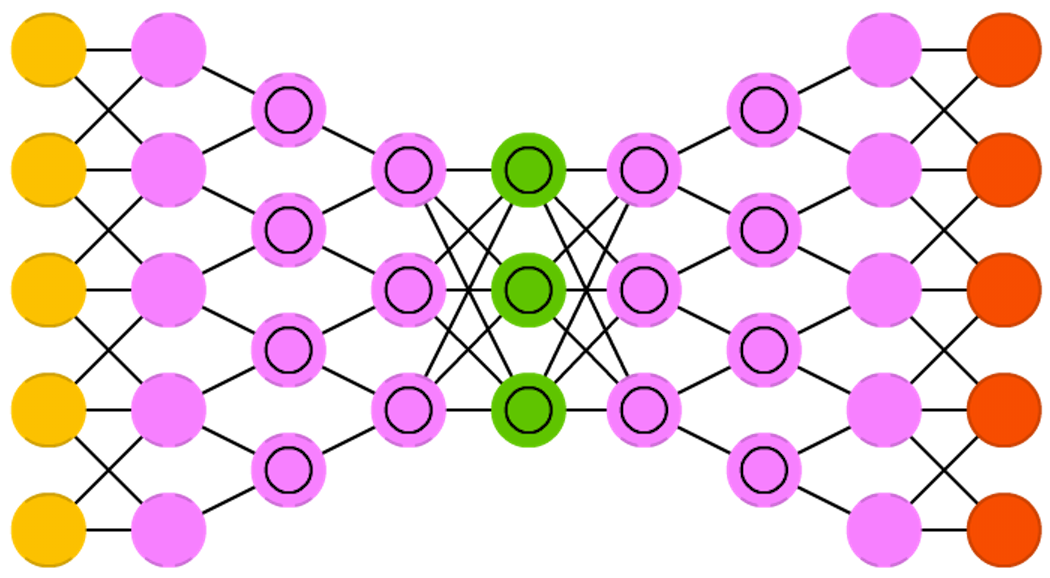
上图是Deep convolutional inverse graphics networks的结构图。DCIGN实际上是一个正向CNN连上一个反向CNN,以实现图片合成的目的。其原理可参考《深度学习(四)》中的Autoencoder。
参见:
http://www.cnblogs.com/pinard/p/6494810.html
卷积神经网络(CNN)反向传播算法
http://blog.csdn.net/zy3381/article/details/44409535
CNN误差反传时旋转卷积核的简明分析
https://mp.weixin.qq.com/s/dnElNURJ6xfWHJVf_yeT8w
理解多层CNN中转置卷积的反向传播
https://www.jianshu.com/p/f0674e48894c
Tensorflow反卷积(DeConv)实现原理

您的打赏,是对我的鼓励
