• Dropout
  • Dropout训练阶段
  • Dropout预测阶段
• 深度学习常用术语解释
  • 深度学习中epoch、batch size、iterations的区别
  • Vanilla
  • weight decay
  • Batch Normalization
  • 鞍点

Dropout

Dropout训练阶段

Dropout是神经网络中解决过拟合问题的一种常见方法。

它的具体做法是：

1.每次训练时，随机隐藏部分隐层神经元。

2.根据样本值，修改未隐藏的神经元的参数。隐藏的神经元的参数保持不变。

3.下次训练时，重新随机选择需要隐藏的神经元。

由于神经网络的非线性，Dropout的理论证明尚属空白，这里只有一些直观解释。

1.dropout掉不同的隐藏神经元就类似在训练不同的网络，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。这实际上就是bagging的思想。

2.因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这会迫使网络去学习更加鲁棒的特征。换句话说，假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的模式（鲁棒性）。

Dropout还有若干变种，如Annealed dropout（Dropout rate decreases by epochs）、Standout（Each neural has different dropout rate）。

---

除了Dropout之外，还有DropConnect。两者原理上类似，后者只隐藏神经元之间的连接。DropConnect也被称作Weight dropout。

总的来说，Dropout类似于机器学习中的L1、L2规则化等增加稀疏性的算法，也类似于随机森林、模拟退火之类的增加随机性的算法。

对drop方法的改进有两种明显的趋势:

随机drop-> 自适应drop

像素级drop -> 区域级drop

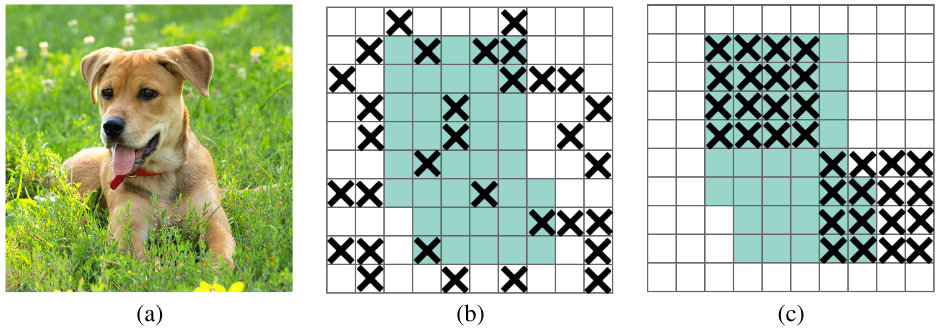
上图是区域级drop的示意图。区域级drop也叫做DropBlock。drop掉一块区域，会迫使网络学习其他区域信息，更有利于提取全局特征。

---

经过dropout之后，输出的均值没有发生变化，但是方差发生了变化。

如果使用了dropout，在训练时隐藏层神经元的输出的方差会与验证时输出的方差不一致，这个方差的变化在经过非线性层的映射之后会导致输出值发生偏移，最终导致了在验证集上的效果很差。

由于回归问题输出是一个绝对值，对这种变化就很敏感，但是分类问题输出只是一个相对的logit，对这种变化就没那么敏感，因此，在回归问题上最好不要用dropout，而在分类问题上才用dropout。

https://zhuanlan.zhihu.com/p/561124500

为什么回归问题不能用Dropout

---

参考：

https://zhuanlan.zhihu.com/p/23178423

Dropout解决过拟合问题

https://mp.weixin.qq.com/s/WvPS9LQ6vfD4OkaRbZ0wBw

如何通过方差偏移理解批归一化与Dropout之间的冲突

https://mp.weixin.qq.com/s/yvwAPmclvgtytfhmETM_mg

Hinton提出的经典防过拟合方法Dropout，只是SDR的特例

https://mp.weixin.qq.com/s/QT7X_ubXS13X5E_5KdbNNQ

谷歌大脑提出DropBlock卷积正则化方法，显著改进CNN精度

https://mp.weixin.qq.com/s/0Go146A5dU0-RESQAaAHzQ

Dropout可能要换了，Hinton等研究者提出神似剪枝的Targeted Dropout

https://mp.weixin.qq.com/s/xmNuUPBuNo6E6XvBA8BR4Q

Dropout的前世与今生

https://mp.weixin.qq.com/s/jFz-2Bdn4dbFAza6MXtroA

Dropout的那些事

https://mp.weixin.qq.com/s/XgiWfRcIMiPUSoadMtAbIg

神经网络Dropout层中为什么dropout后还需要进行rescale？

https://mp.weixin.qq.com/s/L7DwT5LpfWoS474MwWOiLA

华为开源自研算法Disout，多项任务表现更佳

https://zhuanlan.zhihu.com/p/146876678

一文看尽12种Dropout及其变体（在DNN、CNN和RNN中的应用）

https://mp.weixin.qq.com/s/dkIHSRY6Edy8kpFHPJVCOQ

DropBlock正则化的介绍

https://mp.weixin.qq.com/s/g1XSxGG_l7MexuokaChlsQ

理解dropout: 组合 or 噪声？

https://mp.weixin.qq.com/s/n5VXSS_t9JPyLE8UNcWlbA

Drop大法

Dropout预测阶段

经Dropout处理过的模型，在预测阶段不再Dropout，而是打开所有的神经元。这样的效果类似于集成学习，即若干个弱分类器，集成为一个强分类器。

假设p是训练时Dropout的概率。预测阶段由于所有神经元都会参与运算，这会导致\(Wx+b\)是训练阶段的\(\frac{1}{1-p}\)倍，因此需要对W进行相应修正才行，即：

\[W_{ij} \to (1-p)W_{ij}\]

这种修正在预测阶段看来是有些不方便的，因此又出现了Inverted Dropout。它的做法是训练阶段在dropout之后，接上一个除以p的rescale操作，这样的话在预测阶段，就可以忽略dropout操作了。

参考：

https://mp.weixin.qq.com/s/cP8KO3JPIn4lK-n-KdUejA

Dropout有哪些细节问题？

深度学习常用术语解释

深度学习中epoch、batch size、iterations的区别

one epoch：所有的训练样本完成一次Forword运算和BP运算。

batch size：一次Forword运算以及BP运算中所需要的训练样本数目，其实深度学习每一次参数的更新所需要损失函数并不是由一个{data：label}获得的，而是由一组数据加权得到的，这一组数据的数量就是[batch size]。当然batch size越大，所需的内存就越大，要量力而行。

iterations（迭代）：每一次迭代都是一次权重更新，每一次权重更新需要batch size个数据进行Forward运算得到损失函数，再BP算法更新参数。

最后可以得到一个公式one epoch = numbers of iterations = N = 训练样本的数量/batch size

参考：

https://zhuanlan.zhihu.com/p/83626029

浅析深度学习中Batch Size大小对训练过程的影响

Vanilla

Vanilla是神经网络领域的常见词汇，比如Vanilla Neural Networks、Vanilla CNN等。Vanilla本意是香草，在这里基本等同于raw。比如Vanilla Neural Networks实际上就是BP神经网络，而Vanilla CNN实际上就是最原始的CNN。

weight decay

在《机器学习（十四）》中，我们已经指出了规则化在防止病态矩阵中的应用。实际上，规则化也是防止过拟合的重要手段。

\[J(W,b)= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2\]

上式中在普通loss函数后，添加的规则项也被称作weight decay。

weight decay的误差反向传播公式如下：

\[\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) = \left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)}\] \[W^{(l)} = W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right]=(1-\lambda)W^{(l)}-\alpha \left(\frac{1}{m} \Delta W^{(l)} \right)\]

参考：

https://www.zhihu.com/question/24529483

在神经网络中weight decay起到的做用是什么？momentum呢？normalization呢？

Batch Normalization

Batch Normalization是Google提出的一种神经网络优化技巧。

原始论文：

《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》

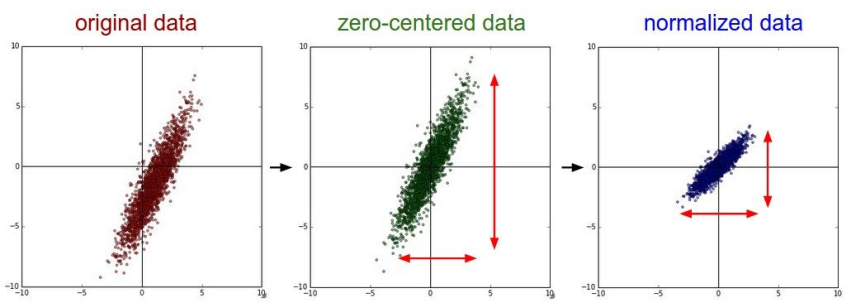
上图直观的展示了Normalize的效果。

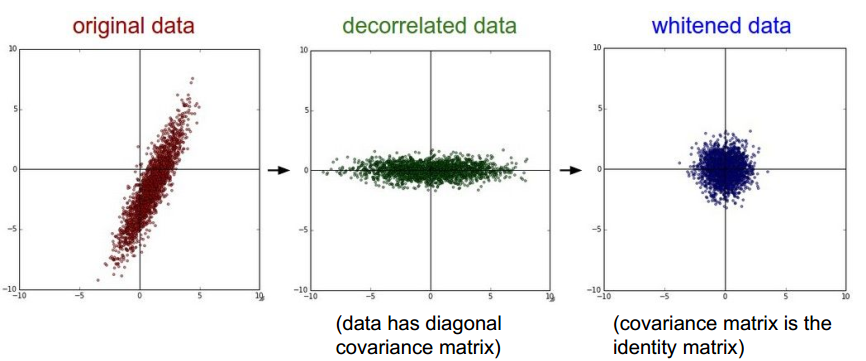
与Normalization相关的概念，还有Decorrelate和Whiten。

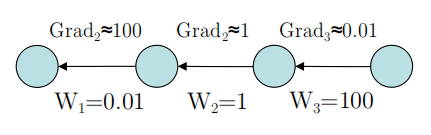
上图是Hinton在2015年的讲座中的例子。从中可以看出，反向传递的梯度大小不仅和激活函数有关，也和每一层的权值大小有关。

通常来说，越靠近输出层，由于该层网络已被充分训练，其权值越大，反之则越小。这实际上也是梯度消失的一种原因。

更一般的，如果一层的权值显著异于相邻的层，从系统的角度出发，这一层也是不稳定的。Normalization将每一层的权值归一化，从而改善了神经网络的性能。它的优点有：

1.提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。

2.提升学习速率。归一化后的数据能够快速的达到收敛。

3.减少模型训练对初始化的依赖。

---

Normalization：

\[x'=\frac{x-\min(x)}{\max(x)-\min(x)}\]

Standardization：

\[x'=\frac{x-\overline{x}}{\sigma}\]

Standardization虽然也能约束取值空间，但没有Normalization那么严格。它的主要目的是将数据映射为正态分布，因此对于异常点，超出\(3\sigma\)也是有可能的。

---

参考：

http://blog.csdn.net/malefactor/article/details/51476961

Batch Normalization导读

http://www.cnblogs.com/neopenx/p/5211969.html

从Bayesian角度浅析Batch Normalization

http://blog.csdn.net/hjimce/article/details/50866313

Batch Normalization学习笔记

https://buptldy.github.io/2016/08/18/2016-08-18-Batch_Normalization/

Implementation of Batch Normalization Layer（中文blog）

https://www.zhihu.com/question/38102762

深度学习中 Batch Normalization为什么效果好？

https://mp.weixin.qq.com/s/OAn8y_uJTgyrtS2ZCyudlg

Batch Normalization原理及其TensorFlow实现

http://blog.csdn.net/u013709270/article/details/70949304

深度神经网络训练的必知技巧

https://mp.weixin.qq.com/s/Oy2GIZLbQxmXMCLzMapWHQ

Batch Normalization的分析与展望

https://www.jianshu.com/p/35a3bf866c46

浅析数据标准化和归一化，优化机器学习算法输出结果

https://blog.csdn.net/u010315668/article/details/80374711

机器学习之特征归一化（normalization）

https://www.jianshu.com/p/95a8f035c86c

归一化（Normalization）、标准化（Standardization）和中心化/零均值化（Zero-centered）

https://mp.weixin.qq.com/s/gWcejm_CMGPKes6tUhbQ5A

BatchNorm的避坑指南

鞍点

在微分方程中，沿着某一方向是稳定的，而另一方向是不稳定的奇点，叫做鞍点（Saddle point）。在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。在矩阵中，一个数在所在行中是最大值，而在所在列中是最小值，则被称为鞍点。在物理上要广泛一些，指在一个方向是极大值，另一个方向是极小值的点。

上图是\(z=x^2-y^2\)的曲面图，其中的原点就是鞍点。上图形似马鞍，故名。