DL » 深度学习(二)——BP算法, 神经元激活函数
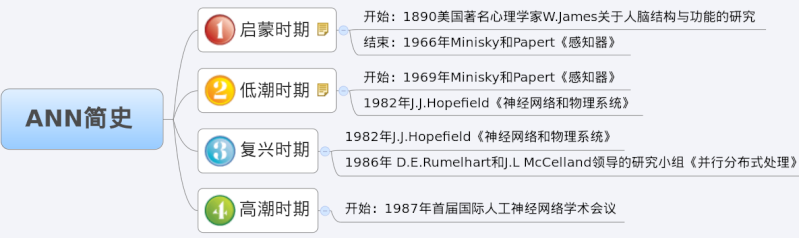
2017-05-17 :: 5827 WordsANN简史
参考:
https://mp.weixin.qq.com/s/0OqqdbUWlWIbfBrRdMs4PA
洪小文:以科学的方式赤裸裸地剖析人工智能:混沌初开
https://mp.weixin.qq.com/s/_G08-3g4QPau2_ZLcsm6-Q
洪小文:以科学的方式赤裸裸地剖析AI(二):从寒冬到复兴
https://mp.weixin.qq.com/s/yWBcK5mEK0AxusVnPt0VNA
洪小文:以科学的方式赤裸裸地剖析AI(三):人的智慧在哪里?
https://mp.weixin.qq.com/s/DkAFMDOnJKkdpV7bnkSZqQ
洪小文:以科学的方式赤裸裸地剖析AI(四):未来是人工智能+人类智能
https://www.visualcapitalist.com/ai-revolution-infographic/
Visualizing the AI Revolution in One Infographic
https://blog.csdn.net/OneFlow_Official/article/details/125013611
深度学习六十年简史
https://mp.weixin.qq.com/s/TfwA4x8dU_rMhC0fuE-xYw
人工智能300年
BP算法
单层神经网络的学习算法最早由Donald Olding Hebb提出,因此又被叫做Hebb算法。但是这种算法无法扩展到多层神经网络,这最终导致了AI的第一个冬天,直到BP算法的出现。
Donald Olding Hebb,1904~1985,加拿大心理学家,哈佛博士(1936),McGill University教授。英国皇家学会会员。神经心理学和神经网络之父。
误差逆传播(error BackPropagation)算法最早由Paul J. Werbos于1974年提出,然而此时正值ANN的低谷,未得到人们的重视。因此到了1986年时,由David Everett Rumelhart重新发明了该算法。
Paul J. Werbos,1947年生,哈佛大学博士。
David Everett Rumelhart,1942~2011,美国心理学家。斯坦福大学博士,先后执教于UCSD和斯坦福。美国科学院院士。
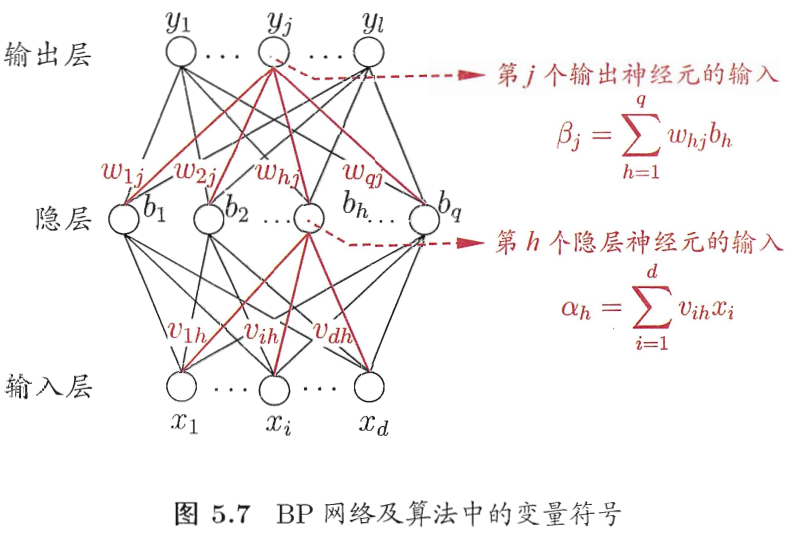
BP算法的核心思路:
1.利用前向传导公式,计算第n层输出值。
2.计算输出值和实际值的残差。
3.将残差梯度传递回第\(n-1,n-2,\dots,2\)层,并修正各层参数。(即所谓的误差逆传播)
BP算法的推导过程教材已经写的很好了,这里只对要点做一个摘录。
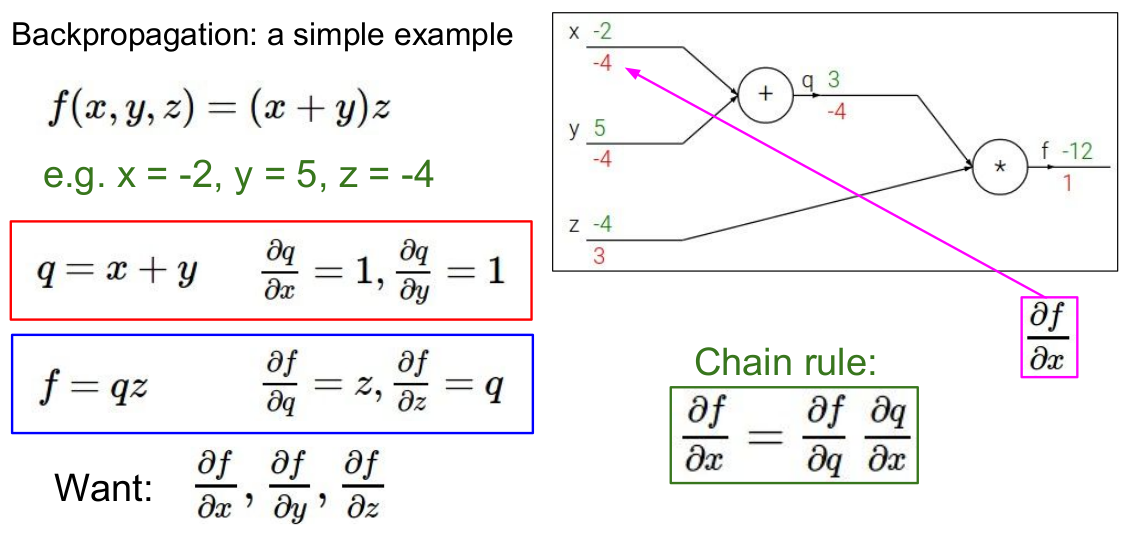
链式法则
Chain Rules本来是微积分中,用于求一个复合函数导数的常用法则。这里用来进行残差梯度的逆传播。
由《机器学习(一)》的公式3可得:
\[\Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}\]\(w_{hj}\)先影响\(\beta_j\),再影响\(\hat y_j^k\),然后影响误差\(E_k\),因此有:
\[\frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat y_j^k}\cdot \frac{\partial \hat y_j^k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial w_{hj}}\tag{1}\]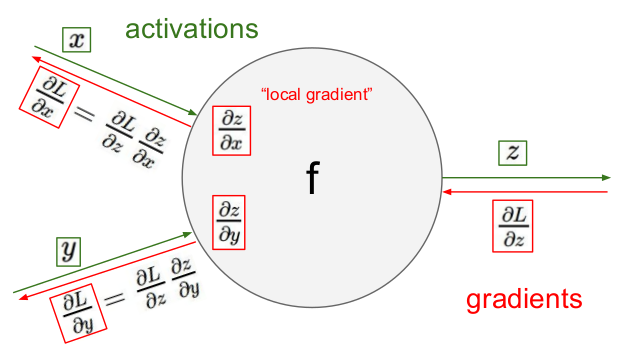
值得注意的是残差梯度实际上包括两部分:\(\Delta x\)和\(\Delta w\)。如下图所示:
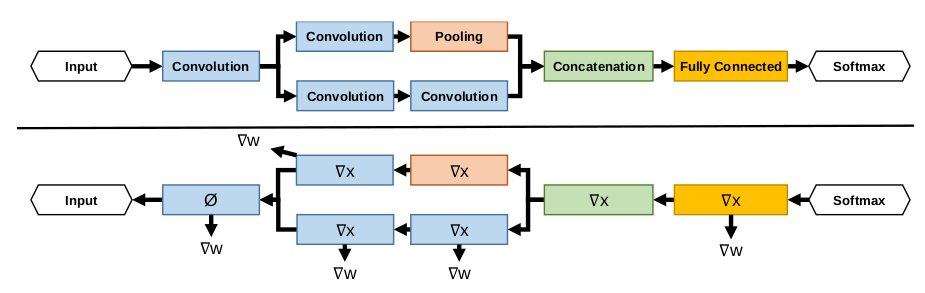
其中,\(\Delta x\)和\(\Delta w\)分别是\(\Delta\)在x和w的偏导数方向上的分量。\(\Delta x\)用于向上层传递梯度,而\(\Delta w\)用于更新权值w。
通常来说,我们只需要更新权值w,但少数情况下,w和x可能都需要更新,这时只要分别计算w和x的偏导,并更新即可。
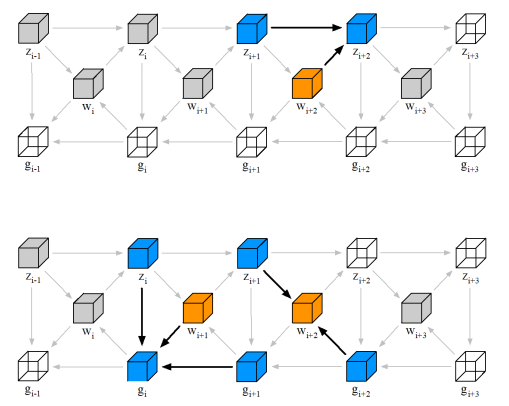
上图是多层MLP的正反向运算关系图。z表示每层的feature map,w表示weight,g表示gradients。上图上半部分展示了正向运算,而下半部分,左侧展示了gradients的更新,右侧展示了weight的更新。
正向计算:
\[\begin{align}& z_{i+1} = z_{i} \cdot w_{i+1}, \\&z_{i} \in R^{M \times K}, w_{i+1} \in R^{K \times N}, z_{i+1} \in R^{M \times N}\end{align}\]Backprop Filter:
\[\begin{align}&\Delta w_{i+1} = z_{i}^T \cdot g_{i+1}, \\& g_{i+1} \text{ is as the same shape as } z_{i+1}\end{align}\]Backprop Input:
\[g_{i} = g_{i+1} \cdot w_{i+1}^T\]从计算量来看,前向计算是2ND,反向是4ND,N为模型参数的数量,D为token总数,2表示一次乘法和一次加法。
除了基于梯度下降的BP算法之外,还有基于GA(genetic algorithm)的BP算法,但基本只有学术界还在尝试。
参考:
https://mp.weixin.qq.com/s/A_Sekyi1kxT1zYcQFBOkDA
Quickprop介绍:一个加速梯度下降的学习方法(由于80/90年代的BP算法收敛缓慢,Scott Fahlman发明了一种名为Quickprop的学习算法。)
https://zhuanlan.zhihu.com/p/25202034
道理我都懂,但是神经网络反向传播时的梯度到底怎么求?
https://mp.weixin.qq.com/s/Ub3CMQszkx7pGKoPcB0bYA
BP反向传播矩阵推导图示详解
https://tech.zealscott.com/deeplearning/11-785/lecture12/
Back propagation through a CNN
https://mp.weixin.qq.com/s/XzyudySeceDueTDM36Q2Wg
学好偏导
https://mp.weixin.qq.com/s/MX8sFKJQZMDMHwkBJ8mCtQ
5种神经网络常见的求导
随机初始化
神经网络的参数的随机初始化的目的是使对称失效。否则的话,所有对称结点的权重都一致,也就无法区分并学习了。
随机初始化的方法有如下几种:
1.Gaussian。用给定均值和方差的Gaussian分布设定随机值。这也是最常用的方法。
2.Xavier。该方法基于Gaussian分布或均匀分布产生随机数。其中分布W的均值为零,方差公式如下:
\[\text{Var}(W)=\frac{1}{n_{in}}\tag{1}\]其中,\(n_{in}\)表示需要输入层的神经元的个数。也有如下变种:
\[\text{Var}(W)=\frac{2}{n_{in}+n_{out}}\tag{2}\]其中,\(n_{out}\)表示需要输出层的神经元的个数。
公式1也被称作LeCun initializer,公式2也被称作Glorot initializer。
3.MSRA。该方法基于零均值的Gaussian分布产生随机数。Gaussian分布的标准差为:
\[\sqrt{\frac{2}{n_l}}\]其中,\(n_l=k_l^2d_{l-1}\),\(k_l\)表示l层的filter的大小,\(d_{l-1}\)表示l-1层的filter的数量。
这种方法也被称作He initializer,是何恺明发明的。
何恺明,清华本科+香港中文大学博士(2011)。先后在MS和Facebook担任研究员。
个人主页:http://kaiminghe.com/
何恺明在训练ResNet的时候发现Xavier方法对于ReLU激活不是太有效,故而提出了新方法。
除了随机初始化之外,还有预训练初始化。比较早期的方法是使用greedy layerwise auto-encoder做无监督学习的预训练,经典代表为Deep Belief Network;而现在更为常见的是有监督的预训练+模型微调。
参考:
https://pouannes.github.io/blog/initialization/
How to initialize deep neural networks? Xavier and Kaiming initialization
https://mp.weixin.qq.com/s/_wt-zTpbd25OL3os0X6cJg
神经网络中的权重初始化一览:从基础到Kaiming
https://mp.weixin.qq.com/s/Nmi4u8LKrsjYKH3_3vmaVQ
神经网络初始化trick:大神何凯明教你如何训练网络!
https://mp.weixin.qq.com/s/DCYusE1lwvm14qpsnPYMpw
初始化:你真的了解我吗?
https://zhuanlan.zhihu.com/p/305055975
kaiming初始化的推导
BP算法的缺点
虽然传统的BP算法,理论上可以支持任意深度的神经网络。然而实际使用中,却很少能支持3层以上的神经网络。
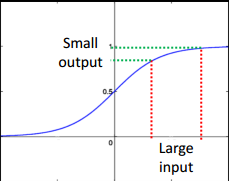
如上图所示,sigmoid函数的特点是左端趋近于0,右端趋近于1,两端都趋于饱和(饱和的定义是导数很接近0)。一个小的输出值的改变,对应了比较大的输入值改变。换句话说,就是输出值的梯度较大,而输入值的梯度较小。而梯度在基于梯度下降的优化问题中,是至关重要的。
随着层数的增多,反向传递的残差梯度会越来越小,这样的现象,被称作梯度消失(Vanishing Gradient)。它导致的结果是,虽然靠近输出端的神经网络已经训练好了,但输入端的神经网络仍处于随机状态。也就是说,靠近输入端的神经网络,有和没有都是一样的效果,完全体现不了深度神经网络的优越性。
和梯度消失相反的概念是梯度爆炸(Vanishing Explode),也就是神经网络无法收敛。
参考:
https://mp.weixin.qq.com/s/w7EbDI9MQBZF67XM-cV1eQ
一文了解神经网络中的梯度爆炸
参考
http://blog.csdn.net/xizero00/article/details/51013088
Different Methods for Weight Initialization in Deep Learning
https://mp.weixin.qq.com/s/xqWli1xnsGkqYDUjgvOnkQ
反向传播神经网络极简入门
https://mp.weixin.qq.com/s/PhxkfWH5bEbykMKGEtDScA
为什么神经网络参数不能够全部初始化为全0?
https://mp.weixin.qq.com/s/s-v7T0k2gy7ZRnrFCUpTYg
通过方差分析详解最流行的Xavier权重初始化方法
https://mp.weixin.qq.com/s/r1OJoLa_t8QwNcL4kfx5uQ
神经网络参数随机初始化已经过时了
https://mp.weixin.qq.com/s/mFA2PeO70o3HR6AQ74Lp3g
深度学习最佳实践之权重初始化
https://mp.weixin.qq.com/s/M1TswiDh-LkH9G7jCQ_UqA
神经网络编程-前向传播和后向传播
https://mp.weixin.qq.com/s/Dygdn0Xzpx40-zUQadiiHg
通过梯度检验帮助实现反向传播
https://mp.weixin.qq.com/s/auNRIPYEwRlROFXug41Ang
简单初始化,训练10000层CNN
https://mp.weixin.qq.com/s/iSJyOe81dnEuaKzOih6WNg
什么是深度学习成功的开始?参数初始化
https://mp.weixin.qq.com/s/s4ew7LYgnC9Z3kVFsjcaXg
不用批归一化也能训练万层ResNet,新型初始化方法Fixup了解一下
https://mp.weixin.qq.com/s/zTB59Fg_JFg9ZZPRlq9txA
不使用残差连接,ICML新研究靠初始化训练上万层标准CNN
https://mp.weixin.qq.com/s/_WCVvM6sPpsWD8NS8etEKA
京东AI研究院提出ScratchDet:随机初始化训练SSD目标检测器
神经元激活函数
tanh函数
除了阶跃函数和Sigmoid函数之外,常用的神经元激活函数,还有双曲正切函数(tanh函数):
\[f(z)=\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\]其导数为:
\[f'(z)=1-(f(z))^2\]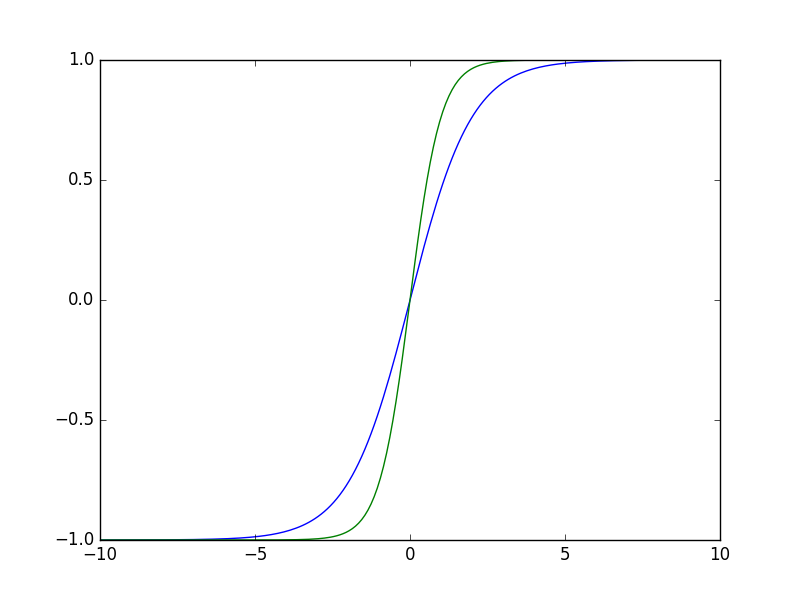
上图是sigmoid函数(蓝)和tanh函数(绿)的曲线图。
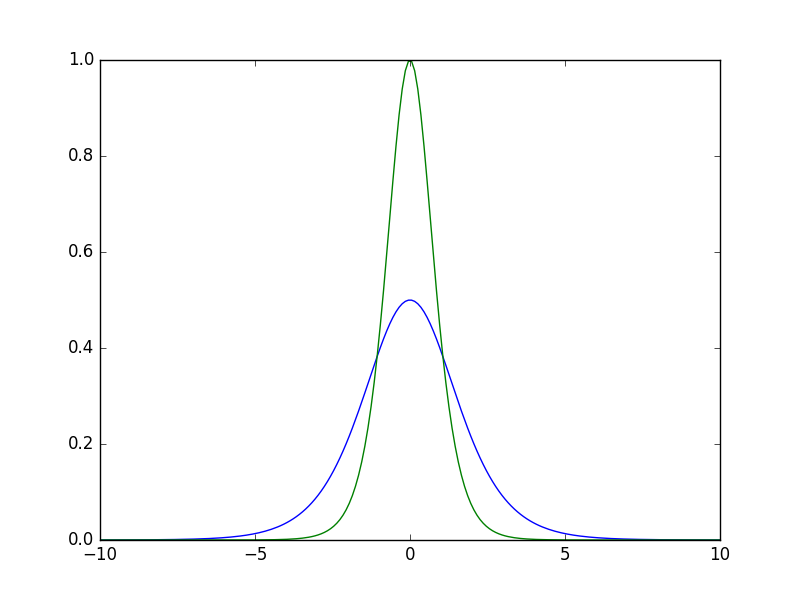
上图是sigmoid函数(蓝)和tanh函数(绿)的梯度曲线图。从中可以看出tanh函数的梯度比sigmoid函数大,因此有利于残差梯度的反向传递,这是tanh函数优于sigmoid函数的地方。但是总的来说,由于两者曲线类似,因此tanh函数仍被归类于sigmoid函数族中。
下图是一些sigmoid函数族的曲线图:
有关sigmoid函数和tanh函数的权威论述,参见Yann LeCun的论文:
http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf

您的打赏,是对我的鼓励

