Antkillerfarm Hacking V7.5

DL » 深度学习（七）——RNN, LSTM

2017-06-22 :: 5925 Words

RNN
LSTM

RNN

RNN的基本结构

RNN是Recurrent Neural Network和Recursive Neural Network的简称。前者主要用于处理和时序相关的输入，而后者目前已经没落。本文只讨论前者。

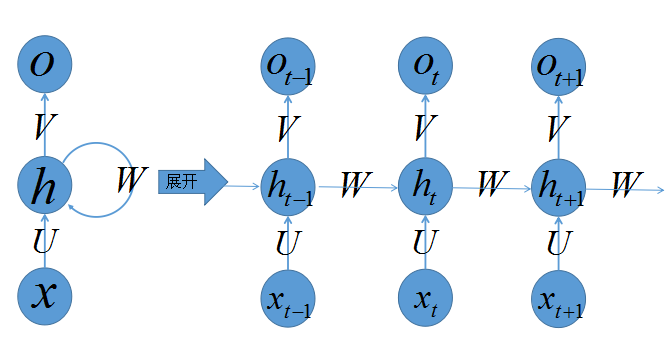
上图是RNN的结构图。其中，展开箭头左边是RNN的静态结构图。不同于之前的神经网络表示，这里的圆形不是单个神经元，而是一层神经元。权值也不是单个权值，而是权值向量。

从静态结构图可以看出RNN实际上和3层MLP的结构，是基本类似的。差别在于RNN的隐藏层多了一个指向自己的环状结构。

上图的展开箭头右边是RNN的时序展开结构图。从纵向来看，它只是一个3层的浅层神经网络，然而从横向来看，它却是一个深层的神经网络。可见神经网络深浅与否，不仅和模型本身的层数有关，也与神经元之间的连接方式密切相关。

虽然理论上，我们可以给每一时刻赋予不同的\(U,V,W\)，然而出于简化计算和稀疏度的考量，RNN所有时刻的\(U,V,W\)都是相同的。

RNN的误差反向传播算法，被称作Backpropagation Through Time（BPTT）。其主要公式如下：

\[\begin{array}\\ \nabla U=\frac{\partial E}{\partial U}=\sum_t\frac{\partial e_t}{\partial U} \\ \nabla V=\frac{\partial E}{\partial V}=\sum_t\frac{\partial e_t}{\partial V} \\ \nabla W=\frac{\partial E}{\partial W}=\sum_t\frac{\partial e_t}{\partial W} \end{array}\]

从上式可以看出，三个误差梯度实际上都是时域的积分。

正因为RNN的状态和过去、现在都有关系，因此，RNN也被看作是一种拥有“记忆性”的神经网络。

RNN的训练困难

理论上，RNN可以支持无限长的时间序列，然而实际情况却没这么简单。

Yoshua Bengio在论文《On the difficulty of training recurrent neural networks》（http://proceedings.mlr.press/v28/pascanu13.pdf）中，给出了如下公式：

\[\left\|\prod_{k<i\le t} \frac{\partial h_{i}}{\partial h_{i-1}}\right\| \le \eta^{t-k}\]

并指出当\(\eta < 1\)时，RNN会Gradient Vanish，而当\(\eta > 1\)时，RNN会Gradient Explode。

这里显然不考虑\(\eta > 1\)的情况，因为Gradient Explode，直接会导致训练无法收敛，从而没有实用价值。

因此有实用价值的，只剩下\(\eta < 1\)了，但是Gradient Vanish又注定了RNN所谓的“记忆性”维持不了多久，一般也就5～7层左右。

上述内容只是一般性的讨论，实际训练还是有很多trick的。

比如，针对\(\eta > 1\)的情况，可以采用Gradient Clipping技术，通过设置梯度的上限，来避免Gradient Explode。

还可使用正交初始化技术，在训练之初就将\(\eta\)调整到1附近。

RNN的历史

上面研究的RNN结构，又被称为Elman RNN。最早是Jeffrey Elman于1990年发明的。

\[\begin{align} h_t &= \sigma_h(W_{h} x_t + U_{h} h_{t-1} + b_h) \\ y_t &= \sigma_y(W_{y} h_t + b_y) \end{align}\]

论文：

《Finding Structure in Time》

Jeffrey Locke Elman，1948年生，Harvard College本科（1969年）+University of Texas博士（1977年）。University of California, San Diego教授，American Academy of Arts and Sciences院士（2015年）。美国心理学会会员。
个人主页：
https://tatar.ucsd.edu/jeffelman/

Harvard College是Harvard University最古老的本部，目前一般提供本科教育。它和其他许多研究生院以及相关部门，共同组成了Harvard University。类似的还有Yale College和Yale University。

American Academy of Arts and Sciences建于1780年。当时，美国正在法国等国的协助下与英国作战，所以美国的创立者选择比照包括作家、人文学者、科学家、军事家、政治家在内的法兰西学术院，建立新大陆的学术院。
后来，林肯总统比照英国皇家学会，于1863年创建了主要涵盖自然科学的National Academy of Sciences，United States。
这两个学院是美国学术界最权威的组织。前者的重要度略高于后者。

美国的创立者，一般被翻译为Founding Fathers of the United States。此外还有一个更响亮的称号76ers。没错，NBA那支球队的名字就是这么来的。

除了Elman RNN之外，还有Jordan RNN。（没错，这就是吴恩达的导师的作品）

\[\begin{align} h_t &= \sigma_h(W_{h} x_t + U_{h} y_{t-1} + b_h) \\ y_t &= \sigma_y(W_{y} h_t + b_y) \end{align}\]

Elman RNN的记忆来自于隐层单元，而Jordan RNN的记忆来自于输出层单元。

参考

http://blog.csdn.net/aws3217150/article/details/50768453

递归神经网络(RNN)简介

http://blog.csdn.net/heyongluoyao8/article/details/48636251

循环神经网络(RNN, Recurrent Neural Networks)介绍

http://mp.weixin.qq.com/s?__biz=MzIzODExMDE5MA==&mid=2694182661&idx=1&sn=ddfb3f301f5021571992824b21ddcafe

循环神经网络

http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/

Backpropagation Through Time算法

https://baijia.baidu.com/s?old_id=560025

Tomas Mikolov详解RNN与机器智能的实现

https://sanwen8.cn/p/3f8sRTh.html

为什么RNN需要做正交初始化？

http://blog.csdn.net/shenxiaolu1984/article/details/71508892

RNN的梯度消失/爆炸与正交初始化

https://mp.weixin.qq.com/s/vHQ1WbADHAISXCGxOqnP2A

看大牛如何复盘递归神经网络！

https://mp.weixin.qq.com/s/0V9DeG39is_BxAYX0Yomww

为何循环神经网络在众多机器学习方法中脱颖而出？

https://mp.weixin.qq.com/s/-Am9Z4_SsOc-fZA_54Qg3A

深度理解RNN：时间序列数据的首选神经网络！

https://mp.weixin.qq.com/s/ztIrt4_xIPrmCwS1fCn_dA

“魔性”的循环神经网络

https://mp.weixin.qq.com/s/BqVicouktsZu8xLVR-XnFg

完全图解RNN、RNN变体、Seq2Seq、Attention机制

https://mp.weixin.qq.com/s/gGGXKT2fTn2xPPvo7PE8IA

像训练CNN一样快速训练RNN：全新RNN实现，比优化后的LSTM快10倍

https://mp.weixin.qq.com/s/OltT-GFDVxaiukb1HVSY3w

通俗讲解循环神经网络的两种应用

https://mp.weixin.qq.com/s/PZMmjT9eXL7rU2pxkQWTiw

从90年代的SRNN开始，纵览循环神经网络27年的研究进展

https://mp.weixin.qq.com/s/7LcqRGPYX6JXpY_0hbjmbA

循环神经网络(RNN)入门帖：向量到序列，序列到序列，双向RNN，马尔科夫化

LSTM

本篇笔记主要摘自：

http://www.jianshu.com/p/9dc9f41f0b29

理解LSTM网络

LSTM结构图

为了解决原始RNN只有短时记忆的问题，人们又提出了一个RNN的变种——LSTM（Long Short-Term Memory）。其结构图如下所示：

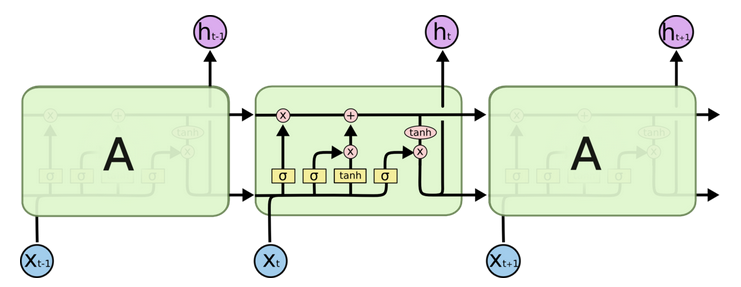
和RNN的时序展开图类似，这里的每个方框表示某个时刻从输入层到隐层的映射。

我们首先回顾一下之前的模型在这里的处理。

MLP的该映射关系为：

\[h=\sigma (W\cdot x+b)\]

RNN在上式基础上添加了历史状态\(h_{t-1}\)：

\[h_t=\sigma (W\cdot [h_{t-1},x_t]+b)\]

LSTM不仅添加了历史状态\(h_{t-1}\)，还添加了所谓的细胞状态\(C_{t-1}\)，即上图中图像上部的水平横线。

步骤详解

神经网络的设计方式和其他算法不同，我们不需要指定具体的参数，而只需要给出一个功能的实现机制，然后借助误差的反向传播算法，训练得到相应的参数。这一点在LSTM上体现的尤为明显。

LSTM主要包括以下4个步骤（也可称为4个功能或门）：

决定丢弃信息

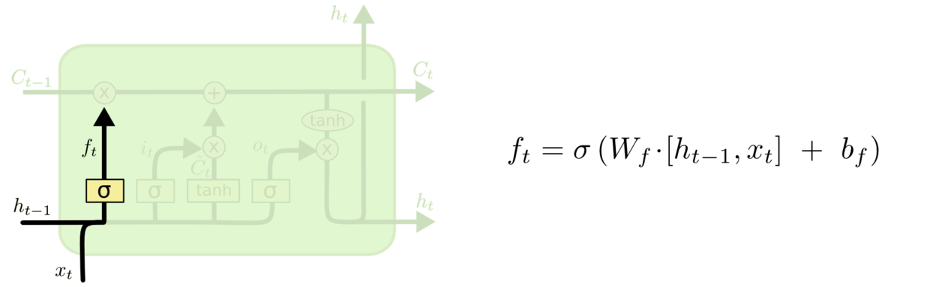
这一部分也被称为忘记门。

确定更新的信息

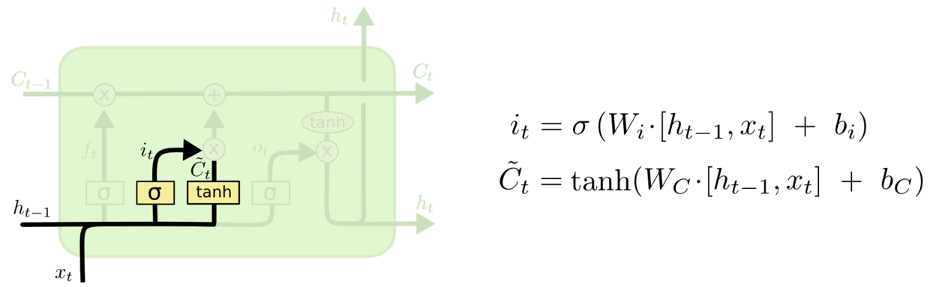
这一部分也被称为输入门。

更新细胞状态

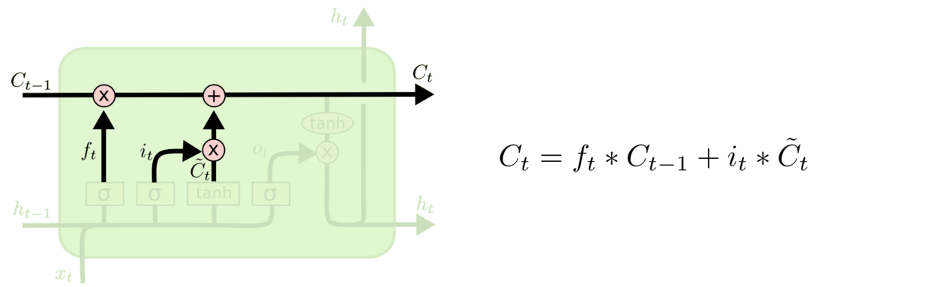
输出信息

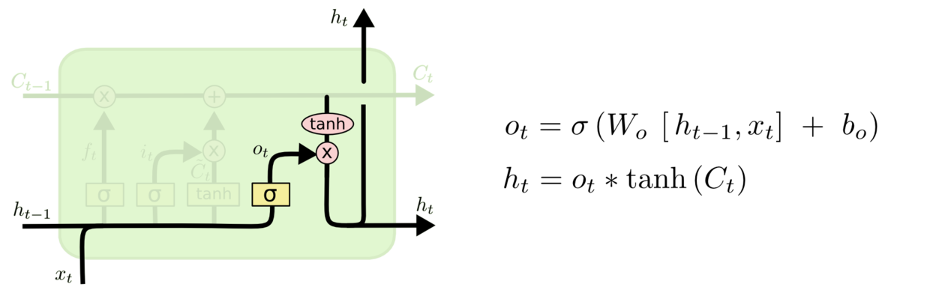
显然，在这里不同的参数会对上述4个功能进行任意组合，从而最终达到长时记忆的目的。

上面的公式中，\(\cdot\)表示Dot product，而\(*\)表示eltwise product。

其他细节

在一般的神经网络中，激活函数可以随意选择，无论是传统的sigmoid，还是新的tanh、ReLU，都不影响模型的大致效果。（差异主要体现在训练的收敛速度上，最终结果也可能会有细微影响。）

但是，上述标准LSTM模型中，tanh函数可以随意替换，而sigmoid函数却不能被替换，切记。

sigmoid用在了各种gate上，产生0~1之间的值，这个一般只有sigmoid最直接了。

tanh用在了状态和输出上，是对数据的处理，这个用其他激活函数也可以。

forget bias的初始值可以设为以1为均值，这对于训练很有好处，这就是tensorflow中forget_bias参数的来历。参见论文：

《An Empirical Exploration of Recurrent Network Architectures》

LSTM的变体

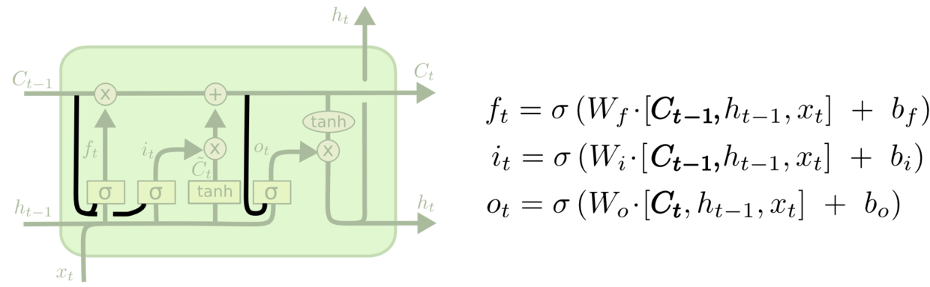
上图中的LSTM变体被称为peephole connection。其实就是将细胞状态加入各门的输入中。可以全部添加，也可以部分添加。

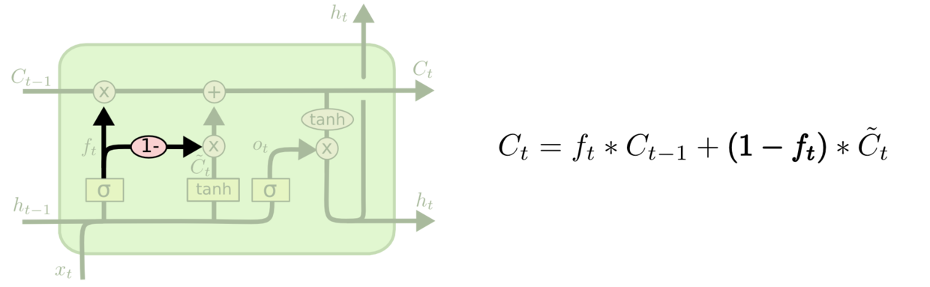
上图中的LSTM变体被称为Coupled Input and Forget Gate（CIFG）。它将忘记和输入门连在了一起。

上图是一个改动较大的变体Gated Recurrent Unit（GRU）。它将忘记门和输入门合成了一个单一的更新门。同样还混合了细胞状态和隐藏状态，和其他一些改动。最终的模型比标准的 LSTM 模型要简单，也是非常流行的变体。

参考

http://www.csdn.net/article/2015-06-05/2824880

深入浅出LSTM神经网络

https://mp.weixin.qq.com/s/y2kV4ye2zr1HYvZd3APeWA

难以置信！LSTM和GRU的解析从未如此清晰

https://blog.csdn.net/zhangxb35/article/details/70060295

RNN, LSTM, GRU公式总结

https://zhuanlan.zhihu.com/p/25821063

循环神经网络——scan实现LSTM

http://blog.csdn.net/a635661820/article/details/45390671

LSTM简介以及数学推导(FULL BPTT)

http://blog.csdn.net/dark_scope/article/details/47056361

RNN以及LSTM的介绍和公式梳理

https://mp.weixin.qq.com/s/x3y9WTuVFYQb60eJvw02HQ

如何解决LSTM循环神经网络中的超长序列问题

https://mp.weixin.qq.com/s/IhCfoabRrtjvQBIQMaPpNQ

从任务到可视化，如何理解LSTM网络中的神经元

https://mp.weixin.qq.com/s/GGpaFZ0crP_NQ564d79hFw

LSTM、GRU与神经图灵机：详解深度学习最热门的循环神经网络

https://mp.weixin.qq.com/s/0bBTVjkfAK2EzQiaFcUjBA

LSTM入门必读：从基础知识到工作方式详解

您的打赏，是对我的鼓励