math » 线性代数（四）——病态矩阵, 矩阵杂谈
2022-01-11 :: 5743 Words病态矩阵
矩阵规则化（续）
Andrey Nikolayevich Tikhonov，1906~1993，苏联数学家和地球物理学家。大地电磁学的发明人之一。苏联科学院院士。著有《Solutions of Ill-posed problems》一书。
更多的V和R取值参见：
https://en.wikipedia.org/wiki/Regularization_(mathematics)
从形式上来看，对比之前提到的拉格朗日函数，我们可以发现规则化因子，实际上就是给损失函数增加了一个约束条件。它的好处是增加了解向量的稳定度，缺点是增加了数值解和真实解之间的误差。
为了更便于理解规则化，这里以二维向量空间为例，给出了规则化因子对损失函数的约束效应。
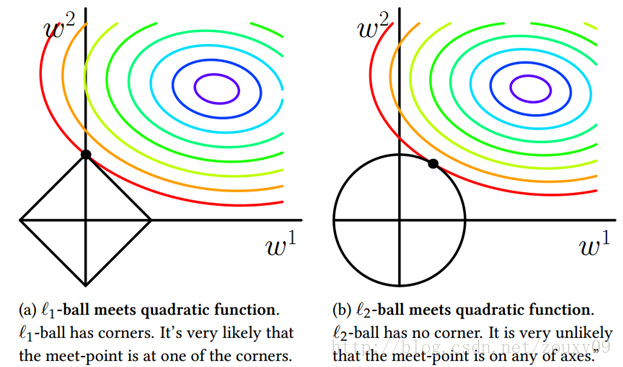
上图中的圆圈是损失函数的等高线，坐标原点是规则化因子的约束中心，左图的方形和右图的圆形是\(l_p\) ball。图中的黑点是等高线和\(l_p\) ball的交点，实际上也就是这个带约束的优化问题的解。
可以看出\(L_1\) regularization的解一般出现在坐标轴上，因而其他坐标上的值就是0，因此，\(L_1\) regularization会导致矩阵的稀疏。
\(L_1\) regularization又被称为Lasso（least absolute shrinkage and selection operator） regression。
从贝叶斯统计的角度来看，规则化相当于增加了一个先验分布，比如\(L_2\) regularization对应的贝叶斯先验分布是Gaussian distribution，而\(L_1\) regularization对应的贝叶斯先验分布是Laplace distribution。
除此之外，还有混合使用规则化的情况，比如：
\[\min_f \sum_{i=1}^nV(f(\hat x_i),\hat y_i)+\lambda \|\beta\|_1 + \eta \|\beta\|_2\]这种方法也被称为弹性网络回归（ElasticNet Regression）。
规则化同时也提供了一种衡量特征重要度的方法：loss函数的值，如果显著小于规则项，则说明该特征不太重要。
参考：
https://en.wikipedia.org/wiki/Tikhonov_regularization
http://www.mit.edu/~cuongng/Site/Publication_files/Tikhonov06.pdf
http://blog.csdn.net/zouxy09/article/details/24971995
机器学习中的范数规则化之（一）L0、L1与L2范数
https://mp.weixin.qq.com/s/pZko9gM5sbFhMl8P8TCFww
机器学习损失函数、L1-L2正则化的前世今生
https://mp.weixin.qq.com/s/pNG8u8V7zp6fLFF9TomEug
史上最全面的正则化技术总结与分析
https://mp.weixin.qq.com/s/PMisvVy4EwEF-5xEY5LrwA
从损失函数的角度详解常见机器学习算法
https://mp.weixin.qq.com/s/MRabAUZrfgD2t2GhnLI43Q
开发者必读：计算机科学中的线性代数
https://mp.weixin.qq.com/s/ctLe1UbvWqBJ8jh-ppU3rA
机器学习中的五种回归模型及其优缺点
https://mp.weixin.qq.com/s/zzCRiSSyfTAFYSGMnr8zfg
机器学习中L1和L2正则化的直观解释
https://mp.weixin.qq.com/s/xwYldlEjJ9Co9uo8o0mlKQ
深度学习之DNN的多种正则化方式
https://mp.weixin.qq.com/s/-axtm6ZBm8yYneiA3mvQrw
SIGIR 2018大会最佳短论文：利用对抗学习的跨域正则化
https://mp.weixin.qq.com/s/FtWA1rff13e7_FM0lJKCVg
Petuum提出新型正则化方法：非重叠促进型变量选择
https://zhuanlan.zhihu.com/p/50142573
L1正则化引起稀疏解的多种解释
https://blog.csdn.net/daunxx/article/details/51596877
Lasso Regression
https://mp.weixin.qq.com/s/kFEwvgBC4-Y05vL3lmRbXQ
正则的一些intuition，一分钟发明新正则
https://mp.weixin.qq.com/s/oZZGBZLRoJVsY7M-CP5MRg
矩阵L2,1/L2,p范数扫盲
https://mp.weixin.qq.com/s/poSfjftItmHERs3MDgvjpw
机器学习防止模型过拟合的方法知识汇总
https://mp.weixin.qq.com/s/YPtGqUXnRQ2qswpBLsbM7g
Lasso和Ridge回归中的超参数调整技巧
矩阵杂谈
矩阵的其他几何意义
https://www.zhihu.com/question/407150749
旋转矩阵为何左乘是相对固定坐标系，右乘是相对当前坐标系？
矩阵的秩
一个矩阵A的列（行）秩是A的线性独立的列（行）的极大数。
下面不加证明的给出矩阵的秩的性质：
1.矩阵的行秩等于列秩，因此可统称为矩阵的秩。
2.秩是n的\(m\times n\)矩阵为列满秩阵；秩是n的\(n\times p\)矩阵为行满秩阵。
3.设\(A\in M_{m\times n}(F)\)，若A是行满秩阵，则\(m\le n\)；若A是列满秩阵 ，则\(n\le m\)。
4.设A为\(m\times n\)列满秩阵，则n元齐次线性方程组\(AX=0\)只有零解。
5.线性方程组\(AX=B\)对任一m维列向量B都有解\(\Leftrightarrow\)系数矩阵A为行满秩阵。
参见：
http://wenku.baidu.com/view/9ce143eb81c758f5f61f6730.html
行(列)满秩阵的几点性质
https://mp.weixin.qq.com/s/N16K511-crzj6h-R1L10rQ
如何通过心形线快速认识秩的几何意义？
奇异矩阵
对应的行列式等于0的方阵，被称为奇异矩阵（singular matrix）。
奇异矩阵和线性相关、秩等概念密切相关。
下面不加证明的给出奇异矩阵的性质：
1.如果A为非奇异矩阵\(\Leftrightarrow\)A满秩。
2.如果A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。如果A为非奇异矩阵，则AX=0有且只有唯一零解，AX=b有唯一解。
对于A不是方阵的情况，一般使用\(A^TA\)来评估矩阵是否是奇异矩阵。
正定矩阵
positive definite matrix的定义：
一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有\(z^TMz>0\)。
正定矩阵A的性质：
1.正定矩阵的任一主子矩阵也是正定矩阵。
2.A的特征值和各阶顺序主子式全为正。
3.若A为n阶正定矩阵，则A为n阶可逆矩阵。
类似的还可以定义负定矩阵、半正定矩阵（非负定矩阵）。
参考：
https://zhuanlan.zhihu.com/p/44860862
浅谈“正定矩阵”和“半正定矩阵”
矩阵与复数
在《特征值和奇异值》一节，我们使用类比的方法，利用复数的性质推导出矩阵的奇异值计算方法和几何含义。
这里我们就要讨论，这个类比为什么能够成立。
复数和矩阵，虽然画起图来（也就是几何意义），颇有相似之处。但从运算上，还是有些差异的。最大的不同就是复数乘法满足交换律，而矩阵乘法不满足交换律。
但是上述结论的后半句，只是针对一般矩阵而言。我们完全可以构造特殊矩阵，使之满足交换律。比如下列矩阵：
\[\begin{bmatrix} a & -b\\ b & a \end{bmatrix} \begin{bmatrix} c & -d\\ d & c \end{bmatrix} =\begin{bmatrix} ac - bd & - ad - bc \\ bc + ad & - bd + ac \end{bmatrix}\] \[\begin{bmatrix} c & -d\\ d & c \end{bmatrix} \begin{bmatrix} a & -b\\ b & a \end{bmatrix} =\begin{bmatrix} ac - bd & - ad - bc \\ bc + ad & - bd + ac \end{bmatrix}\]我们不妨根据这个现象，构建复数和矩阵映射关系：
\[z=a+bi \Leftrightarrow Z = \begin{bmatrix} a & -b\\ b & a \end{bmatrix}\]这个映射，不仅能满足乘法交换律，还可以满足其他的复数运算：
\[\overline z=a-bi \Leftrightarrow \overline Z = \begin{bmatrix} a & b\\ -b & a \end{bmatrix}\] \[\frac{1}{z}=\frac{\overline z}{|z|^2} \Leftrightarrow Z^{-1} = \frac{\overline Z}{|Z|}\]当然，还是有一个不满足的：
\[|Z| = |z|^2\]数学上，一般把满足相同运算规则的运算集合称为群。复数和它的二阶矩阵拥有相同的运算规则，则他们拥有相同的性质，也就不足为奇了。
自由度问题：粗看起来二阶矩阵有4个元素，也就是有4个自由度，然而由于元素之间的关系，实际上只有a和b两个元素，也就是2个自由度。这正好与复数相同。
使用二阶矩阵便于对具体的复数运算，产生直观的定义和理解。比如波动理论中的振幅与相位是两个独立的变量，使用复数还需要思考复平面到底是怎么回事，而使用二阶矩阵对应好两个自由度，就没有这样的心智上的压力了。
Q：既然复数和它的二阶矩阵等价，那为什么不用矩阵运算代替复数运算？
A：复数运算不仅和各种代数方程有关联，性质更为丰富，而且计算量也比二阶矩阵小。
上面讨论的是二阶矩阵的元素为实数的情况，如果上述二阶矩阵的元素为复数的话，则构成的代数便是四元数。四元数可以用来描述\(R^3\)上的旋转，由此，矩阵代表法可看成代数的凯莱-迪克森结构法。
https://zhuanlan.zhihu.com/p/355325102
矩阵与复数
https://www.zhihu.com/question/62524302
虚数的现实、物理意义是什么？
行列式与迹
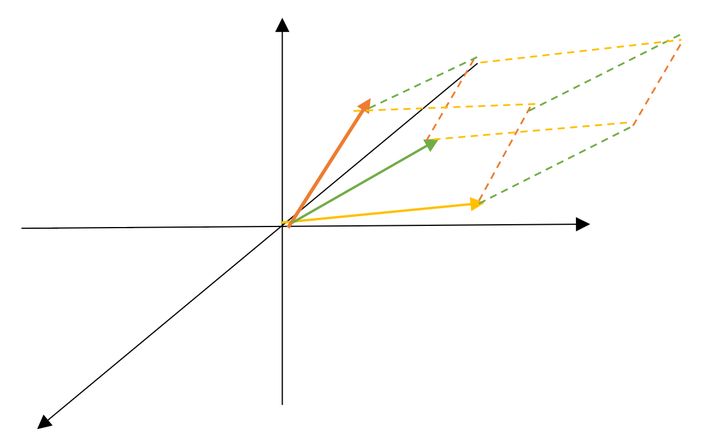
三个向量张成了一个平行六面体，而A的行列式的绝对值即为其体积。
行列式和迹，都属于矩阵的阿贝尔不变量（abelian invariants）。
由于某种神秘原因，大家学线性代数的时候一般都会忽略迹（可能是因为太好算了，把矩阵的对角线元素加起来就行了，老师出不了题目）。其实迹在某种意义上更”本质”。因为如果说行列式对应着”体积”，那么迹对应着”维数”。在数学（表示论等等）和物理（量子场论等等）中，我们都会发现迹无处不在。尤其是无限维矩阵的迹。
https://www.zhihu.com/question/36966326
行列式的本质是什么？
https://zhuanlan.zhihu.com/p/19609459
矩阵的秩与行列式的几何意义
线性方程组
对应于主元位置的变量称为基本变量，其余变量称为自由变量。
https://zhuanlan.zhihu.com/p/387925183
齐次线性方程组
Krylov subspace
Krylov subspace是一类针对大矩阵的近似计算的方法，由Aleksey Nikolaevich Krylov于1931年提出。
Aleksey Nikolaevich Krylov，1863～1945，俄罗斯海军工程师、数学家、作家。
参考：
https://blog.csdn.net/lizhengjiang/article/details/18794275
krylov子空间迭代法
https://www.zhihu.com/question/23309010
如何使用Krylov方法求解矩阵的运算尤其是逆？
数学杂谈
高斯给出了正十七边形可以尺规作图的理论可能性，然而他并不会做。第一个真正的正十七边形尺规作图法直到1825年才由约翰尼斯·厄钦格（Johannes Erchinger）给出。现在比较通行的做法是1893年Herbert William Richmond给出的。距离高斯给出证明（1801年），差不多过了100年。
陈景润只是证明了维诺格拉多夫的方法技巧已经做到了尽头。
https://mp.weixin.qq.com/s/68K3L_pD7xfobr_jA1QgWA
陈景润究竟为证明哥德巴赫猜想做出了哪些贡献？
李萨如曲线（Lissajous Curve）：两个沿着互相垂直方向的正弦振动合成的轨迹。
https://mp.weixin.qq.com/s/RwG8HaK02-Fa0t26UboD7w
用数学方式打开Facebook新Logo，真的和视频号Logo来自同一方程
您的打赏，是对我的鼓励
