• LU分解（续）
• 特征值和奇异值
  • QR分解
  • 矩阵的特征值和特征向量
  • QR算法
  • 矩阵的奇异值

LU分解（续）

这里只介绍一下Doolittle算法。

\[A=\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \dots & \dots & \dots & \dots \\ a_{n1} & a_{n2} & \dots & a_{nn} \\ \end{bmatrix}=LU= \begin{bmatrix} 1 & 0 & \dots & 0 \\ l_{21} & 1 & \dots & 0 \\ \dots & \dots & \dots & \dots \\ l_{n1} & l_{n2} & \dots & 1 \\ \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & \dots & u_{1n} \\ 0 & u_{22} & \dots & u_{2n} \\ \dots & \dots & \dots & \dots \\ 0 & 0 & \dots & u_{nn} \\ \end{bmatrix}\]

由矩阵乘法定义，可知：

\[a_{1j}=u_{1j},j=1,2,\dots,n\] \[a_{ij}=\begin{cases} \sum_{t=1}^jl_{it}u_{tj}, & j<i \\ \sum_{t=1}^{i-1}l_{it}u_{tj}+u_{ij}, & j\ge i \\ \end{cases}\]

因此：

\(u_{1j}=a_{1j},j=1,2,\dots,n\)（U的第1行）
\(l_{j1}=a_{j1}/u_{11},j=1,2,\dots,n\)（L的第1列）
For \(i=2,3,\dots,n\) do

\(u_{ii}=a_{ii}-\sum_{t=1}^{i-1}l_{it}u_{tj}\)
\(u_{ij}=a_{ij}-\sum_{t=1}^{i-1}l_{it}u_{tj}\),for \(j=i+1,\dots,n\)（U的第i行）
\(l_{ji}=\frac{a_{ji}-\sum_{t=1}^{i-1}l_{jt}u_{ti}}{u_{ii}}\),for \(j=i+1,\dots,n\)（L的第i列）

End
\(u_{nn}=a_{nn}-\sum_{t=1}^{n-1}l_{nt}u_{tn}\)

参见：

http://www3.nd.edu/~zxu2/acms40390F11/Alg-LU-Crout.pdf

特征值和奇异值

QR分解

任意实数方阵A，都能被分解为\(A=QR\)。这里的Q为正交单位阵，即\(Q^TQ=I\)。R是一个上三角矩阵。这种分解被称为QR分解。

QR分解也有若干种算法，常见的包括Gram–Schmidt、Householder和Givens算法。

Jørgen Pedersen Gram，1850～1916，丹麦数学家，在矩阵、数论、泛函等领域皆有贡献。他居然是被自行车撞死的…

Erhard Schmidt，1876～1959，德国数学家，哥廷根大学博士，柏林大学教授。David Hilbert的学生。20世纪数学界的几位超级大神之一。1933年前的哥廷根大学数学系，秒杀其他所有学校。所谓“一流的学生去哥廷根，智商欠费才去藤校”。

Alston Scott Householder，1904～1993，美国数学家，芝加哥大学博士，田纳西大学教授。ACM主席。

James Wallace Givens, Jr.，1910～1993，美国数学家，普林斯顿大学博士，西北大学教授。参与UNIVAC I机器项目（1951年），这是最早的商用计算机。

这里只介绍Gram–Schmidt算法，这个算法虽然名为Gram–Schmidt，然而拉普拉斯和柯西早就已经用过了。

首先介绍一下向量的投影运算的符号表示。

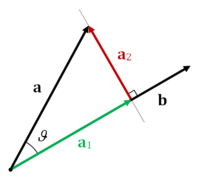
如上图所示，根据余弦定理和向量点乘的定义可得：

\[a\cdot b=\mid a\mid \mid b\mid \cos \theta\]

因此，向量a在向量b上的投影向量\(a_1\)，可表示为：

\[a_1=\mid a\mid \cos \theta\hat b=\mid a\mid \frac{a\cdot b}{\mid a\mid \mid b\mid }\frac{b}{\mid b\mid }=\frac{a\cdot b}{\mid b\mid ^2}b=\frac{a\cdot b}{b\cdot b}b=\frac{\langle a,b\rangle}{\langle b,b\rangle}b\]

特别的，当b为单位向量时：

\[a_1=\langle a,b\rangle\tag{1}\]

我们定义投影符号如下：

\[\mathrm{proj}_{\mathbf{e}}\mathbf{a} = \frac{\left\langle\mathbf{e},\mathbf{a}\right\rangle}{\left\langle\mathbf{e},\mathbf{e}\right\rangle}\mathbf{e}\]

令\(A=[\mathbf{a}_1, \cdots, \mathbf{a}_n]\)，其中\(a_i\)为列向量。则：

\[\begin{align} \mathbf{u}_1 &= \mathbf{a}_1, & \mathbf{e}_1 &= {\mathbf{u}_1 \over \|\mathbf{u}_1\|} \\ \mathbf{u}_2 &= \mathbf{a}_2-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{a}_2, & \mathbf{e}_2 &= {\mathbf{u}_2 \over \|\mathbf{u}_2\|} \\ \mathbf{u}_3 &= \mathbf{a}_3-\mathrm{proj}_{\mathbf{u}_1}\,\mathbf{a}_3-\mathrm{proj}_{\mathbf{u}_2}\,\mathbf{a}_3, & \mathbf{e}_3 &= {\mathbf{u}_3 \over \|\mathbf{u}_3\|} \\ & \vdots &&\vdots \\ \mathbf{u}_k &= \mathbf{a}_k-\sum_{j=1}^{k-1}\mathrm{proj}_{\mathbf{u}_j}\,\mathbf{a}_k, &\mathbf{e}_k &= {\mathbf{u}_k\over\|\mathbf{u}_k\|} \end{align}\]

即：

\[\begin{align} \mathbf{a}_1 &= \langle\mathbf{e}_1,\mathbf{a}_1 \rangle \mathbf{e}_1 \\ \mathbf{a}_2 &= \langle\mathbf{e}_1,\mathbf{a}_2 \rangle \mathbf{e}_1 + \langle\mathbf{e}_2,\mathbf{a}_2 \rangle \mathbf{e}_2 \\ \mathbf{a}_3 &= \langle\mathbf{e}_1,\mathbf{a}_3 \rangle \mathbf{e}_1 + \langle\mathbf{e}_2,\mathbf{a}_3 \rangle \mathbf{e}_2 + \langle\mathbf{e}_3,\mathbf{a}_3 \rangle \mathbf{e}_3 \\ &\vdots \\ \mathbf{a}_k &= \sum_{j=1}^{k} \langle \mathbf{e}_j, \mathbf{a}_k \rangle \mathbf{e}_j \end{align}\]

这个过程又被称为Gram–Schmidt正交化过程。

因此：

\[Q = \left[ \mathbf{e}_1, \cdots, \mathbf{e}_n\right] \qquad \text{and} \qquad R = \begin{bmatrix} \langle\mathbf{e}_1,\mathbf{a}_1\rangle & \langle\mathbf{e}_1,\mathbf{a}_2\rangle & \langle\mathbf{e}_1,\mathbf{a}_3\rangle & \ldots \\ 0 & \langle\mathbf{e}_2,\mathbf{a}_2\rangle & \langle\mathbf{e}_2,\mathbf{a}_3\rangle & \ldots \\ 0 & 0 & \langle\mathbf{e}_3,\mathbf{a}_3\rangle & \ldots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix}\]

矩阵的特征值和特征向量

设A是一个n阶方阵，\(\lambda\)是一个数，如果方程\(Ax=\lambda x\)存在非零解向量，则称\(\lambda\)为A的一个特征值（Eigenvalue），相应的非零解向量x称为属于特征值\(\lambda\)的特征向量（eigenvector）。

上面这个描述也可以记作：

\[(A-\lambda I)x=0\tag{2}\]

这个公式本身通常用于：已知特征值，求解对应的特征向量。

其中，\(A-\lambda I\)被称为特征矩阵，而\(\lvert A-\lambda I \rvert=0\)被称为特征方程。求解特征方程可得到特征值。

特征值和特征向量在有的书上也被称为本征值和本征向量。

特征值和特征向量的特性包括：

1.特征向量属于特定的特征值，离开特征值讨论特征向量是没有意义的。不同特征值对应的特征向量不会相等，但特征向量不能由特征值唯一确定。

2.在复数范围内，n阶矩阵A有n个特征值。在这些特征值中，模最大的那个特征值即主特征值（对于实数阵即绝对值最大的特征值），主特征值对应的特征向量称为主特征向量。

更多内容参见：

http://course.tjau.edu.cn/xianxingdaishu/jiao/5.htm

矩阵的特征值和特征向量

https://mp.weixin.qq.com/s/mZ4AeCcoU0LhWRWfa9_kvw

花了10分钟，终于弄懂了特征值和特征向量到底有什么意义

https://mp.weixin.qq.com/s/uL5fCNTegK9ST2LOO13-4g

图说幂法求特征值和特征向量

QR算法

对矩阵A进行QR分解可得：\(A=QR\)

因为Q是正交阵（\(Q^T=Q^{-1}\)），所以正交相似变换\(Q^TAQ\)和A有相同的特征值。

证明：

\[\begin{array}\\ \mid Q^TAQ-\lambda I\mid =\mid Q^TAQ-Q^T(\lambda I)Q\mid =\mid Q^T(A-\lambda I)Q\mid \\ =\mid Q^T\mid \cdot\mid A-\lambda I\mid \cdot\mid Q\mid =\mid Q^TQ\mid \cdot\mid A-\lambda I\mid =\mid I\mid \cdot\mid A-\lambda I\mid =\mid A-\lambda I\mid \end{array}\]

这里的证明，用到了行列式的如下性质：

\[\mid I\mid =1\] \[\mid AB\mid =\mid A\mid \cdot\mid B\mid\]

因为\(Q^TAQ\)和A的特征方程相同，所以它们的特征值也相同。证毕。

由此产生如下迭代算法：

Repeat until convergence {

1.\(A_k=Q_kR_k\)（QR分解）
2.\(A_{k+1}=Q_k^TA_kQ_k=Q_k^{-1}Q_kR_kQ_k=R_kQ_k\)

}

这个算法的收敛性证明比较复杂，这里只给出结论：

\[\lim_{k\to\infty}A_k=\begin{bmatrix} \lambda_1 & u_{12} & \dots & u_{1n} \\ 0 & \lambda_2 & \dots & u_{2n} \\ \dots & \dots & \ddots & \dots \\ 0 & 0 & \dots & \lambda_n \end{bmatrix}\]

其中，\(\lambda_i\)为矩阵的特征值。\(u_{ij}\)表示任意值，它们的极限可能并不存在。

QR算法于1961年，由John G.F. Francis和Vera Nikolaevna Kublanovskaya发现。

John G.F. Francis，1934年生，英国计算机科学家，剑桥大学肄业生。
2000年，QR算法被IEEE计算机学会评为20世纪的top 10算法之一。然而直到那时，计算机界的数学家们竟然都没有见过Francis本尊，连这位大神是活着还是死了都不知道，仿佛他在发表完这篇惊世之作后就消失了一般。
2007年，学界的两位大牛：Gene Howard Golub（SVD算法发明人之一，后文会提到。）和Frank Detlev Uhlig（1972年获加州理工学院博士，Auburn University数学系教授），经过不懈努力和人肉搜索终于联系上了他。
他一点都不知道自己N年前的研究被引用膜拜了无数次，得知自己的QR算法是二十世纪最NB的十大算法还有点小吃惊。这位神秘大牛竟然连TeX和Matlab都不知道。现在这位大牛73岁了，活到老学到老，还在远程教育大学Open University里补修当年没有修到的学位。
2015年，University of Sussex授予他荣誉博士学位。
相关内容参见：
http://www.netlib.org/na-digest-html/07/v07n34.html

Vera Nikolaevna Kublanovskaya，1920~2012，苏联数学家，女。终身供职于苏联科学院列宁格勒斯塔克罗夫数学研究所。52岁获得博士学位。

Steklov的故事，参见《数学狂想曲（六）》。这里顺便说一下，苏联的博士学位问题。苏联有个“副博士”的学位，这是一名学生通过学历教育所能获得的最高学位。苏联的博士学位无法通过教育获得，而只能根据成果评定，因此难度大大超过欧美的博士，一般只有教授级人物才能获得。
简单来说就是：
苏联副博士=欧美博士
苏联博士=欧美教授
所以，Kublanovskaya实际上还是很牛的人物。

需要指出的是，QR算法可求出矩阵的所有特征值，如果只求某一个特征值的话，还有其他一些更快的算法。详见：

https://en.wikipedia.org/wiki/Eigenvalue_algorithm

矩阵的奇异值

在进一步讨论之前，我们首先介绍一下矩阵特征值的几何意义。

首先，矩阵是对线性变换的表示，确定了定义域空间V与目标空间W的两组基，就可以很自然地得到该线性变换的矩阵表示。

线性空间变换的几何含义如下图所示：

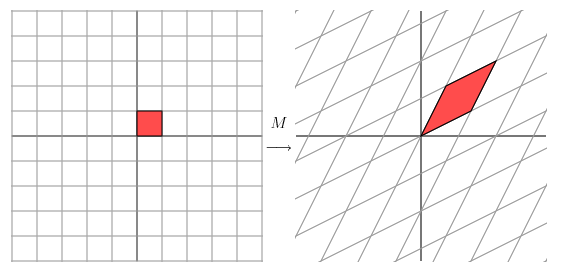
图中的坐标轴，就是线性空间的基。

线性变换主要有三种几何效果：旋转、缩放、投影。