• 边缘检测（续）
  • 波纹算子
  • 直线算子
• 边界闭合
• canny算法
  • 非最大抑制
  • 双阈值（Double Thresholding）
  • 滞后的边界跟踪
• 距离变换
• 锐化
  • 梯度锐化
  • 拉普拉斯锐化
• 图像金字塔
  • 高斯金字塔
  • 拉普拉斯金字塔
  • Steerable金字塔
• 双边滤波（Bilateral filter）
• 导向滤波
• Steerable滤波
• Gabor滤波
  • 基、线性无关、正交
  • Gabor wavelet
  • Gabor filter

边缘检测（续）

波纹算子

\[s_x=\left[\begin{array}{ccc} 0&-1&d\\ 1&0&-1 \\ -d&1&0\end{array} \right],s_y=\left[\begin{array}{ccc} d&-1&0\\ -1&0&1 \\ 0&1&-d\end{array} \right]\]

对称梯度算子和波纹算子都属于边缘子空间基。

直线算子

\[s_x=\left[\begin{array}{ccc} 0&1&0\\ -1&0&-1 \\ 0&1&0\end{array} \right],s_y=\left[\begin{array}{ccc} -1&0&1\\ 0&0&0 \\ 1&0&-1\end{array} \right]\]

直线算子和拉普拉斯算子都属于直线子空间基。

边界闭合

如果像素\((s,t)\)在像素\((x,y)\)的领域，且满足以下条件：

\[\mid G(s,t)-G(x,y)\mid \le 幅度阀值T\] \[\mid \theta(s,t)-\theta(x,y)\mid \le 角度阀值A\]

则可将像素\((s,t)\)和像素\((x,y)\)连接起来。

canny算法

Canny边缘检测算子是John F.Canny于1986年开发出来的一个多级边缘检测算法。

John F. Canny，1958年生，澳大利亚计算机科学家。MIT博士，UCB教授。

1.应用高斯滤波来平滑图像，目的是去除噪声。

2.找寻图像的强度梯度（intensity gradients)

3.应用非最大抑制（non-maximum suppression）技术来消除边误检（本来不是但检测出来是）。

4.应用双阈值的方法来决定可能的（潜在的）边界。

5.利用滞后技术来跟踪边界。

1、2的基本原理，上面已经讨论过了，这里不再赘述。

非最大抑制

图中的数字代表了像素点的梯度强度，箭头方向代表了梯度方向。以第二排第三个像素点为例，由于梯度方向向上，则将这一点的强度（7）与其上下两个像素点的强度（5和4）比较，由于这一点强度最大，则保留。

双阈值（Double Thresholding）

设定一个阈值上界和阈值下界，图像中的像素点如果大于阈值上界，则认为必然是边界（称为强边界，strong edge），小于阈值下界则认为必然不是边界，两者之间的，被认为是候选项（称为弱边界，weak edge）。

滞后的边界跟踪

和强边界相连的弱边界认为是边界，其他的弱边界则被抑制。

参考：

http://www.cse.iitd.ernet.in/~pkalra/csl783/canny.pdf

距离变换

距离变换(distance transform)是一种将二值图像灰度化的变换。

方法：

首先对图像进行二值化处理（这里的二值化通常是边缘检测后的结果），然后给每个像素赋值为离它最近的边界像素点与其的距离（Manhattan距离或欧氏距离），以得到distance metric(距离矩阵)，那么离边界越远的点越亮。

效果图：

这种效果通常叫做羽化效果。

常用的距离公式有：

\[\rho(r)=\frac{r^2}{2}\] \[\rho(r)=r\] \[\rho(r)=2\left(\sqrt{1+\frac{r^2}{2}}-1\right)\] \[\rho(r)=C^2\left(\frac{r}{C}-log\left(1+\frac{r}{C}\right)\right),C=1.3998\] \[\rho(r)=\frac{C^2}{2}\left[1-\exp\left(-\left(\frac{r}{C}\right)^2\right)\right],C=2.9846\]

锐化

锐化是与模糊相反的图像操作，它的主要思想是增大图像色彩（或灰度）的对比度，简单的说就是：让亮的更亮，让暗的更暗。因此，锐化操作和边缘检测有很大的共同点，常用的锐化算法有梯度锐化和拉普拉斯锐化。

梯度锐化

\[g=\begin{cases} f+C, & G>T \\ f, & G\le T \\ \end{cases}\]

当像素\((x,y)\)的梯度G大于阀值T时，在旧的像素值f上加上常数C，否则，保持原值。

拉普拉斯锐化

\[g=f+\nabla^2f\]

其中\(\nabla^2f\)表示f的二阶导数。

图像金字塔

一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。

图像金字塔在机器视觉和图像压缩领域使用的比较多，比如OpenGL中的纹理处理。

图像金字塔有两种基本操作：

1.对图像向上采样：PyrUp——图像尺寸加倍。

2.对图像向下采样：PyrDown——图像尺寸减半。

这两种操作由于是针对图像尺寸而言的，因此，其方向和上图所示的金字塔的方向相反。

高斯金字塔

高斯金字塔是通过高斯平滑和亚采样获得一些列下采样图像，也就是说第K层高斯金字塔通过平滑、亚采样就可以获得K+1层高斯图像，高斯金字塔包含了一系列低通滤波器，其截至频率从上一层到下一层是以因子2逐渐增加，所以高斯金字塔可以跨越很大的频率范围。

拉普拉斯金字塔

一般来说，由于PyrDown的过程会损失部分图像信息，因此通常情况下：

\[G_i\neq PyrUp(PyrDown(G_i))\]

为了使PyrUp和PyrDown可逆，这里引入拉普拉斯金字塔的概念。其定义如下：

\[L_i=G_i-PyrUp(G_{i+1})=G_i-Up(G_{i+1})\otimes H_{5\times 5}\]

其中UP操作是将源图像中位置为(x,y)的像素映射到目标图像的(2x+1,2y+1)位置，\(H_{5\times 5}\)表示5x5的高斯核。

整个拉普拉斯金字塔运算过程可以通过下图来概括：

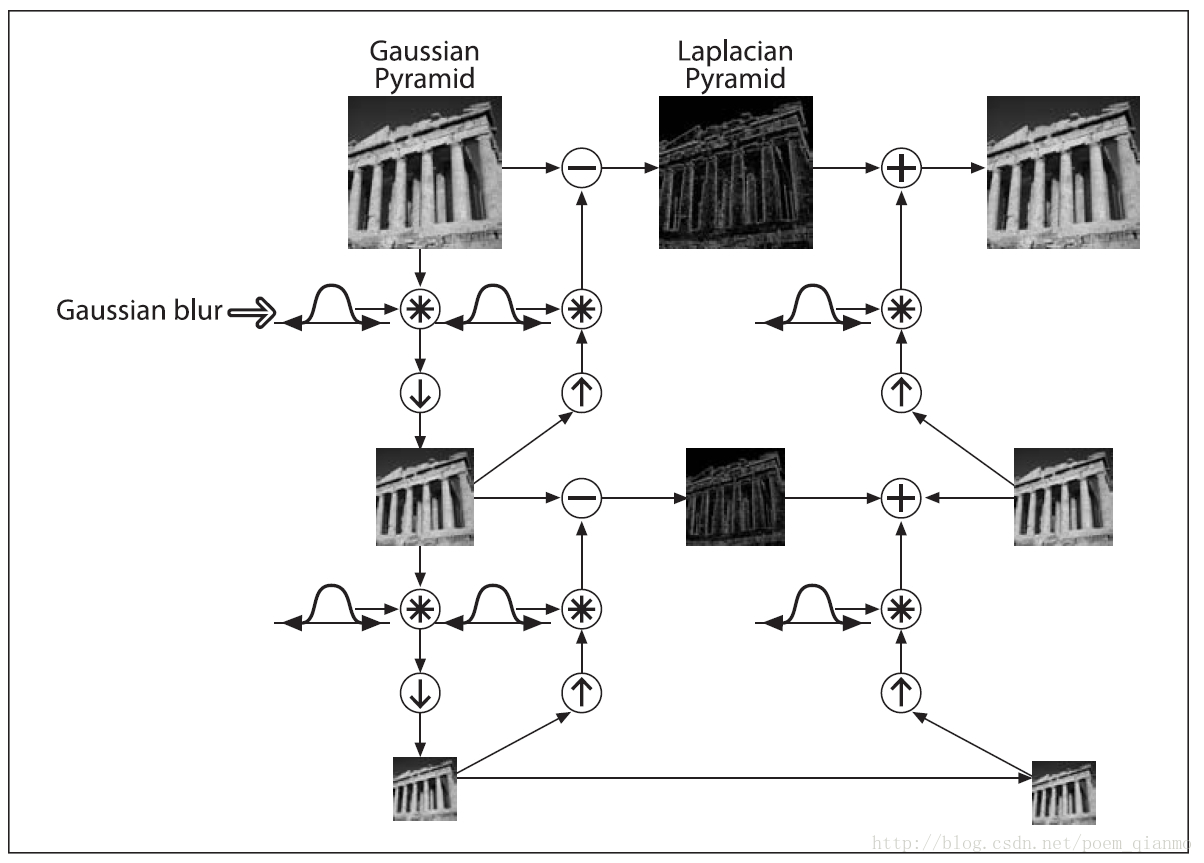
图中最左列和最右列都是高斯金字塔，中间一列是拉普拉斯金字塔。

严格来说，这样的金字塔应该叫做高斯差分金字塔，只不过高斯差分恰好是拉普拉斯算子的近似解，故名。

参考：

https://mp.weixin.qq.com/s/d17B0KaevV1LJDNgxgPLhg

深度优化局部拉普拉斯金字塔滤波器

Steerable金字塔

将拉普拉斯金字塔中的高斯滤波函数，换成Steerable滤波函数即可。

双边滤波（Bilateral filter）

双边滤波（Bilateral filter）是一种可以保边去噪的滤波器。其输出像素的值依赖于邻域像素的值的加权组合，即：

\[g(i,j)=\frac{\sum_{k,l}f(k,l)w(i,j,k,l)}{\sum_{k,l}w(i,j,k,l)}\]

也就是：

\[h=\frac{w(i,j,k,l)}{\sum_{k,l}w(i,j,k,l)}\]

其中，

\[w(i,j,k,l)=d(i,j,k,l)\cdot r(i,j,k,l)=\exp\left(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}\right)\cdot \exp\left(-\frac{\|f(i,j)-f(k,l)\|^2}{2\sigma_r^2}\right)\]

这里的\(d(i,j,k,l)\)由于只与定义域有关，通常叫做“定义域核”。实际上，这就是一个高斯滤波核。而\(r(i,j,k,l)\)由于和像素值的差有关（像素差越大，权重越小），也被叫做“值域核”。

从效果来说，双边滤波可产生类似美肤的效果。皮肤上的皱纹和斑，与正常皮肤的差异，远小于黑白眼珠之间的差异，因此前者被平滑，而后者被保留。

为了体现效果，这里来张大叔的照片。

参考：

https://mp.weixin.qq.com/s/JbrZRTwkI7yeC5hOr8g_Mw

Bilateral Solver双边算子原理及应用

https://zhuanlan.zhihu.com/p/310710051

pytorch实现双边滤波

导向滤波

https://blog.csdn.net/weixin_43194305/article/details/88959183

导向滤波(Guided Filter)公式详解

https://zhuanlan.zhihu.com/p/161666126

导向滤波原理（Guided Filter）

https://zhuanlan.zhihu.com/p/279602383

四种图像滤波算法实现及原理解析

Steerable滤波

高斯滤波是一种各向同性滤波，如果想要对特定方向进行滤波的话，可使用Steerable滤波。

对最简二维高斯函数\(G(x,y)=e^{-(x^2+y^2)}\)求1阶偏导可得：

\[G_1^0=\frac{\partial G(x,y)}{\partial x}=-2xe^{-(x^2+y^2)},G_1^{\frac{\pi}{2}}=\frac{\partial G(x,y)}{\partial y}=-2ye^{-(x^2+y^2)}\]

这就是两个轴向上的1阶Steerable滤波函数。

任意角度的1阶Steerable滤波函数为：

\[G_1^{\theta}=\cos\theta G_1^0+\sin\theta G_1^{\frac{\pi}{2}}\]

如果对高斯函数求2阶偏导,还可得到2阶Steerable滤波函数。进一步的讨论详见参考论文。

参考：

1991年IEEE论文：《The Design and Use of Steerable Filters》

作者：William T. Freeman，斯坦福大学本科+斯坦福/康奈尔大学双料硕士+麻省理工学院博士，麻省理工学院教授。1987年，曾做为访问学者在太原理工大学待了一学年。不知道爱不爱吃刀削面(^ω^)

Edward H. Adelson，密歇根大学博士，麻省理工学院教授。

Gabor滤波

基、线性无关、正交

一般的函数可以展开为幂级数或者Fourier级数。这些级数中的幂函数或者正弦函数，被称作“基(basis)函数”。

基的属性主要涉及“线性无关”和“正交”这两个名词。

线性无关的几何含义：在\(R^3\)(3维空间)中，如果三个向量不共面，则它们相互线性无关。

基如果线性无关，则其函数的级数展开式是唯一的。由于线性相关基使用的比较少，以下如无特指，基均为线性无关基。

正交的几何含义：两个向量正交，则它们是相互垂直的。

正交基一定线性无关，反之则不成立。一般采用施密特正交化方法，将线性无关基，转换为正交基。

幂级数是线性无关基，而Fourier级数是正交基。

Gabor wavelet

除了以上两种常用的基函数外，其他函数也可以作为基函数。其中使用最多的基函数是小波(wavelet)函数，其变换也被称作小波变换。

需要指出的是，小波函数不是一个函数，而是一类函数。Gabor函数就是小波函数的其中一种，其定义如下：

\[g_{t,n}(x)=g(x-al)e^{2\pi ibnx},-\infty<l,n<+\infty\]

这里的\(a,b\)为常数，\(g\)为\(L^2(R)\)(立方可积函数)，且\(\parallel g\parallel=1\)。

Dennis Gabor（1900~1979），全息学创始人，1971年获诺贝尔物理学奖，著有《Theory of Communication》（1946）。

当\(g\)为高斯函数时，可得到Gabor wavelet：

\[f(x)=e^{-(x-x_0)^2/a^2}e^{-ik_0(x-x_0)}\]

Gabor wavelet的性质：

1.Gabor wavelet的Fourier变换还是Gabor wavelet：

\[F(k)=e^{-(k-k_0)^2a^2}e^{-ix_0(k-k_0)}\]

2.从物理上来说，Gabor wavelet等效于在一个正弦载波（频域）上，调制一个高斯函数（时空域）。这也是Dennis Gabor最早提出它的时候的用途。

3.Fourier变换是信号在整个时域内的积分，因此反映的是信号频率的统计特性，没有局部化分析信号的功能。而Gabor变换是一种短时Fourier变换，具有良好的时频局部化特性，即非常容易地调整Gabor滤波器的方向、基频带宽及中心频率，从而能够最好的兼顾信号在时空域和频域中的分辨能力。

Gabor filter

将Gabor wavelet扩展到2维，可得到Gabor filter(图像实际上就是一种2维信号)：

\[g(x,y;\lambda,\theta,\psi,\sigma,\gamma)=\exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\exp\left(i\left(2\pi\frac{x'}{\lambda}+\psi\right)\right)\]

其中，

\[x'=x\cos\theta+y\sin\theta,y'=-x\sin\theta+y\cos\theta\]