ML » 机器学习(十二)——因子分析
2016-09-16 :: 7688 Words因子分析
之前的讨论都是基于样本个数m远大于特征数n的,现在来看看\(m\ll n\)的情况。
这种情况本质上意味着,样本只覆盖了很小一部分的特征空间。当我们应用高斯模型的时候,会发现协方差矩阵\(\Sigma\)根本就不存在,自然也就没法利用之前的方法了。
那么我们应该怎么办呢?
对\(\Sigma\)的限制
有两种方法可以对\(\Sigma\)进行限制。
方法一:
设定\(\Sigma\)为对角线矩阵,即所有非对角线元素都是0。其对角线元素为:
\[\Sigma_{jj}=\frac{1}{m}\sum_{i=1}^m(x_j^{(i)}-\mu_j)^2\]二维多元高斯分布在平面上的投影是个椭圆,中心点由\(\mu\)决定,椭圆的形状由\(\Sigma\)决定。\(\Sigma\)如果变成对角阵,就意味着椭圆的两个轴都和坐标轴平行了。
方法二:
还可以进一步约束\(\Sigma\),可以假设对角线上的元素都是相等的,即:
\[\Sigma=\sigma^2I\]其中:
\[\sigma=\frac{1}{mn}\sum_{j=1}^n\sum_{i=1}^m(x_j^{(i)}-\mu_j)^2\]这实际上也就是方法一中对角线元素的均值,反映到二维高斯分布图上就是椭圆变成圆。
当我们要估计出完整的\(\Sigma\)时,我们需要\(m\ge n+1\)才能保证在最大似然估计下得出的\(\Sigma\)是非奇异的。然而在上面的任何一种假设限定条件下,只要\(m\ge 2\)就可以估计出限定的\(\Sigma\)。
这样做的缺点也是显而易见的,我们认为特征间相互独立,这个假设太强。接下来,我们给出一种称为因子分析(factor analysis)的方法,使用更多的参数来分析特征间的关系,并且不需要计算一个完整的\(\Sigma\)。
利用多元高斯分布密度函数计算积分的技巧
\[I(A,b,c)=\int_x\exp\left(-\frac{1}{2}(x^TAx+x^Tb+c)\right)\mathrm{d}x\]其中A为对称正定矩阵,b为向量。对于上面这样的积分,可以使用“完全配方法”(completion-of-squares)的数学技巧求解。
因为
\[x^TAx+x^Tb+c=(x-h)^TA(x-h)+k\]其中\(h=-\frac{A^{-1}b}{2},k=c-\frac{b^TA^{-1}b}{4}\)。
所以
\[\begin{align} I(A,b,c)&=\int_x\exp\left(-\frac{1}{2}((x - h)^TA(x - h)+k)\right)\mathrm{d}x \\&=\int_x\exp\left(-\frac{1}{2}(x - h)^TA(x - h)-k/2\right)\mathrm{d}x \\&=\exp(-k/2)\cdot\int_x\exp\left(-\frac{1}{2}(x - h)^TA(x - h)\right)\mathrm{d}x \end{align}\]令\(\mu=h,\Sigma=A^{-1}\),则:
\[I(A,b,c)=\frac{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}{\exp(k/2)}\cdot\int_x\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)\mathrm{d}x\]公式右侧的被积分函数,正好是多元高斯分布密度函数,因此该积分值为1。于是:
\[I(A,b,c)=\frac{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}{\exp(k/2)}\]原始讲义里,Chuong B. Do写的《Gaussian processes》的附录A.1和本节内容类似,但推导过程有问题,疑似笔误,特更换为维基百科中的例子。(矩阵的完全配方那块的变换,我能推导出维基百科的结果,但推导不出Chuong B. Do的结果。)如有错误,望读者指出。
边缘和条件高斯分布
假设x由两个随机向量组成(可以看作是将之前的\(x^{(i)}\)分成了两部分)。
\[x=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\]其中\(x_1\in R^r,x_1\in R^s\),则x实际上是\(r+s\)维向量。
假设\(x\sim N(\mu,\Sigma)\),其中:
\[\mu=\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix},\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}\]因为协方差矩阵是对称矩阵,因此\(\Sigma_{12}=\Sigma_{21}^T\)。
\[\begin{align} Cov(x)&=\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} \\&=E\begin{bmatrix} (x-\mu)(x-\mu)^T \end{bmatrix}=E\begin{bmatrix} \begin{pmatrix} x_1-\mu_1 \\ x_2-\mu_2 \end{pmatrix} & \begin{pmatrix} x_1-\mu_1 \\ x_2-\mu_2 \end{pmatrix} \end{bmatrix} \\&=E\begin{bmatrix} (x_1-\mu_1)(x_1-\mu_1)^T & (x_1-\mu_1)(x_2-\mu_2)^T \\ (x_2-\mu_2)(x_1-\mu_1)^T & (x_2-\mu_2)(x_2-\mu_2)^T \end{bmatrix} \end{align}\]因此,\(E[x_1]=\mu_1,Cov(x_1)=E[(x_1-\mu_1)(x_1-\mu_1)^T]=\Sigma_{11}\)。可见,多元高斯分布的边缘分布仍然是多元高斯分布。
下面讨论一下条件高斯分布。
\[\begin{align} p(x_1\mid x_2)&=\frac{p(x_1,x_2)}{p(x_2)}=\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma\rvert^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)}{\int_{x_1}p(x_1,x_2;\mu,\Sigma)\mathrm{d}x_1} \\&=\frac{1}{Z_1}\exp\left\{-\frac{1}{2}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)^T\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)\right\} \end{align}\]其中的\(Z_1\)是和\(x_1\)无关的部分,可看作常数,下面的\(Z_i\)也是同理。
\[\Sigma^{-1}=V=\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}\]因为:
\[\begin{align} &\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right)^T\begin{bmatrix} V_{11} & V_{12} \\ V_{21} & V_{22} \end{bmatrix}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}-\begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\right) \\&=(x_1-\mu_1)^TV_{11}(x_1-\mu_1)+(x_1-\mu_1)^TV_{12}(x_2-\mu_2) \\&\qquad+(x_2-\mu_2)^TV_{21}(x_1-\mu_1)+(x_2-\mu_2)^TV_{22}(x_2-\mu_2) \end{align}\]保留上式中与\(x_1\)有关的部分,可得:
\[p(x_1\mid x_2)=\frac{1}{Z_2}\exp\left(-\frac{1}{2}\left(x_1^TV_{11}x_1-2x_1^TV_{11}\mu_1+2x_1^TV_{12}(x_2-\mu_2)\right)\right)\]使用上一节中的完全配方技巧,可得:
\[p(x_1\mid x_2)=\frac{1}{Z_3}\exp\left(-\frac{1}{2}(x_1-\mu_{1\mid 2})^TV_{11}(x_1-\mu_{1\mid 2})\right)\]其中:
\[\mu_{1\mid 2}=\mu_1-V_{11}^{-1}V_{12}(x_2-\mu_2)\tag{1}\]即:
\[x_1\mid x_2\sim N(\mu_1-V_{11}^{-1}V_{12}(x_2-\mu_2),V_{11}^{-1})\]另,根据分块矩阵的求逆法则,可得:
\[\Sigma^{-1}=\begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}^{-1}=\begin{bmatrix} (\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1} & -(\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1}\Sigma_{12}\Sigma_{22}^{-1} \\ -\Sigma_{22}^{-1}\Sigma_{21}(\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})^{-1} & (\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12})^{-1} \end{bmatrix}\]因此:
\[\Sigma_{1\mid 2}=V_{11}^{-1}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}\tag{2}\]因子分析的例子
下面通过一个简单例子,来引出因子分析背后的思想。
假设我们有m=5个2维的样本点\(x^{i}\),如下:
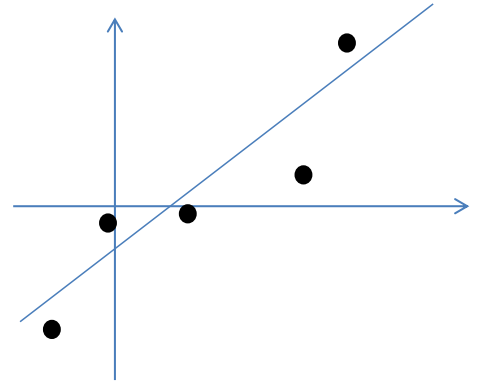
按照因子分析模型,样本点的生成过程如下:
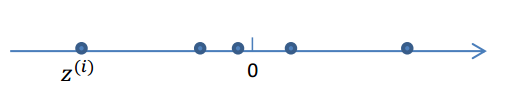
1.我们首先认为在1维空间(这里k=1),存在着按正态分布生成的m个点\(z^{(i)}\),即:
\[z^{(i)}\sim N(0,I)\]这里的I是单位矩阵。
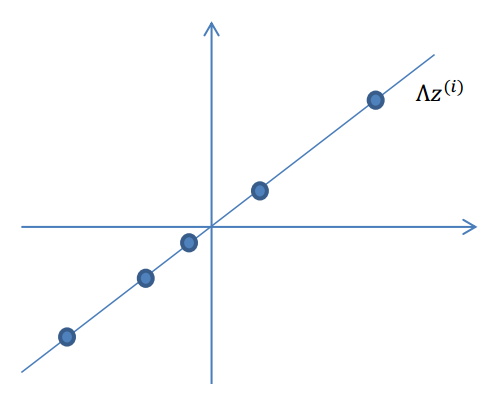
2.使用变换矩阵\(\Lambda\in R^{n\times k}\),将\(z^{(i)}\)映射到n维空间中,即\(\Lambda z^{(i)}\)。
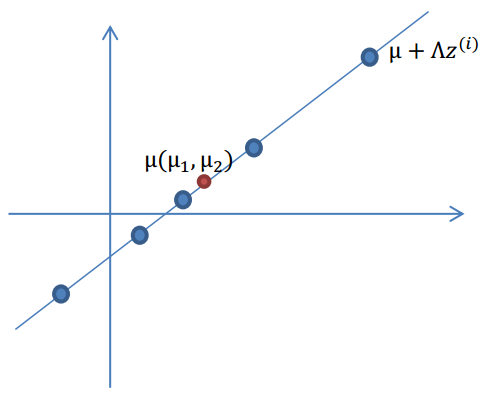
3.使用n维向量\(\mu\),将\(\Lambda z^{(i)}\)移动到样本的中心点\(\mu\),即\(\mu+\Lambda z^{(i)}\)
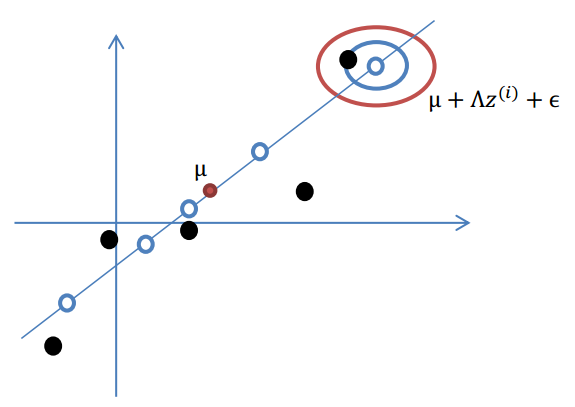
4.样本点不可能这么规则,在模型上会有一定偏差,因此我们需要将上步生成的点做一些扰动(误差)。这里添加一个n维的扰动向量\(\epsilon \sim N(0,\Psi)\)。
综上可得:
\[x^{(i)}=\mu+\Lambda z^{(i)}+\epsilon\] \[x \mid z\sim N(\mu+\Lambda z,\Psi)\]由以上的直观分析,我们知道了因子分析其实就是认为:高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的,因此高维数据可以使用低维来表示。
线性回归的概率模型
在进一步讨论因子分析模型之前,我们首先讨论一下,和它类似的线性回归的概率模型。
从概率的角度看,线性回归中的\(y^{(i)}\)可以看作是预测函数\(h_\theta(x)\)加上扰动后的结果。即:
\[y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)},\epsilon^{(i)}\sim N(0,\sigma^2)\] \[p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right)\] \[p(y^{(i)}\mid x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right)\] \[\begin{align} \ell(\theta)&=\log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right)=\sum_{i=1}^m\log\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}\right) \\&=m\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-\theta^Tx^{(i)}\right)^2 \end{align}\]从上式可以看出采用极大似然估计和采用代价函数\(J(\theta)\)的效果是一样的。其中:
\[J(\theta)=\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-\theta^Tx^{(i)}\right)^2\]因子分析模型
假设z和x的联合分布为:
\[\begin{bmatrix} z \\ x \end{bmatrix}\sim N(\mu_{zx},\Sigma)\]我们的任务就是求出\(\mu_{zx}\)和\(\Sigma\)。
因为:
\[E[x]=E[\mu+\Lambda z+\epsilon]=\mu+\Lambda E[z]+E[\epsilon]=\mu\]所以:
\[\mu_{zx}=\begin{bmatrix} \vec{0} \\ \mu \end{bmatrix}\]因为:
\[\Sigma=\begin{bmatrix} \Sigma_{zz} & \Sigma_{zx} \\ \Sigma_{xz} & \Sigma_{xx} \end{bmatrix}\]所以我们只要分别计算这四个值即可。
因为\(z\sim N(0,I)\),所以\(\Sigma_{zz}=I\)。
\[\begin{align} \Sigma_{zx}&=E[(z-E[z])(x-E[x])^T]=E[(z-0)(\mu+\Lambda z+\epsilon-\mu)^T]=E[z(\Lambda z+\epsilon)^T] \\&=E[z(\Lambda z)^T+z\epsilon^T]=E[zz^T\Lambda^T+z\epsilon^T]=E[zz^T]\Lambda^T+E[z\epsilon^T] \end{align}\]因为z和\(\epsilon\)是相互独立的随机变量,因此\(E[z\epsilon^T]=E[z]E[\epsilon^T]=0\)。
又因为\(E[zz^T]=Cov(z)=I\),所以\(\Sigma_{zx}=\Lambda^T\)。
\[\begin{align} \Sigma_{xx}&=E[(x-E[x])(x-E[x])^T]=E[(\mu+\Lambda z+\epsilon-\mu)(\mu+\Lambda z+\epsilon-\mu)^T] \\&=E[(\Lambda z+\epsilon)(\Lambda z^T+\epsilon^T)]=E[\Lambda z(\Lambda z)^T+\epsilon(\Lambda z)^T+\Lambda z\epsilon^T+\epsilon\epsilon^T] \\&=E[\Lambda zz^T\Lambda^T+\epsilon z^T\Lambda^T+\Lambda z\epsilon^T+\epsilon\epsilon^T] \\&=\Lambda E[zz^T]\Lambda^T+E[\epsilon z^T]\Lambda^T+\Lambda E[z\epsilon^T]+E[\epsilon\epsilon^T] \\&=\Lambda I\Lambda^T+0+0+\Psi=\Lambda \Lambda^T+\Psi \end{align}\]
您的打赏,是对我的鼓励
