ML » 机器学习(八)——学习理论
2016-08-31 :: 6629 Words学习理论
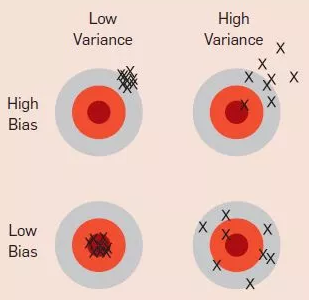
偏差和方差
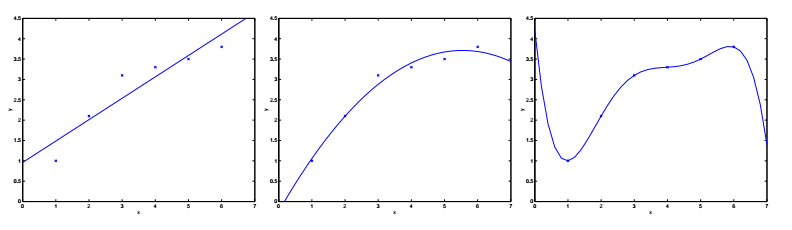
回到之前的欠拟合与过拟合的例子。我们把预测值和实际值之间的误差称为泛化误差。注意:泛化误差不是拟合模型和训练样本值之间的差,后者通常被称作模型误差。
偏差(bias)和方差(variance)都是泛化误差(generalization error)的组成部分。但遗憾的是,这两个名词至今也没有公认的严格定义,这里只做定性的描述,即:欠拟合的误差主要是偏差,而过拟合的误差主要是方差。
学习理论的预备知识
学习理论(learning theory)主要解决三大问题:
1.偏差和方差的权衡。这实际上是模型选择的问题。如何才能自动确定模型的阶数呢?
2.如何关联模型误差和泛化误差?
3.如何确定我们的学习算法是有效的?
首先介绍两个定理:
The union bound定理:
如果\(A_1,\dots,A_k\)是k个不同的事件,则:
\[P(A_1\cup \dots\cup A_k)\le P(A_1)+\dots+P(A_k)\]Hoeffding不等式:
\(Z_1,\dots,Z_m\)是m个独立且具有相同分布的随机变量(independent and identically distributed,IID)。如果它们满足Bernoulli(\(\phi\))分布,即\(P(Z_i=1)=\phi,P(Z_i=0)=1-\phi\),则:
\[P(\lvert\phi-\hat\phi\rvert>\gamma)\le 2\exp(-2\gamma^2m)\]其中,\(\hat\phi=(1/m)\sum_{i=1}^mZ_i\),\(\gamma\)是大于0的任意常数。
这个不等式是Wassily Hoeffding于1963年证明的。它表明样本数量越大,则随机变量的平均值越接近其数学期望值。
Wassily Hoeffding,1914~1991,芬兰统计学家,柏林大学博士,无偏统计学(U-statistics)创始人。
这个不等式在统计学领域也叫做Chernoff bound,但实际上是Herman Chernoff的朋友Herman Rubin发现的。他们的关系有点像苹果公司的那两个Steve,都是统计学领域的巨擘。
Herman Chernoff,1923年生,美国数学家、物理学家,布朗大学博士,先后执教于MIT和哈佛。
Herman Rubin,1926年生,美国数学家,21岁获得芝加哥大学的博士学位。现为普渡大学教授。
Herman Chernoff写过一篇文章回忆他和Herman Rubin的友谊,其中提到后者IQ 180,比他牛多了。其实,Herman Chernoff 24岁获得博士学位,也是妥妥的学霸级人物。
以下假定y的取值为0或1,则:
\[\hat\varepsilon(h)=\frac{1}{m}\sum_{i=1}^m1\{h(x^{(i)})\neq y^{(i)}\}\]\(\hat\varepsilon(h)\)被称作训练误差(training error),也叫做经验风险(empirical risk)或经验误差(empirical error),它表征的是在训练样本集上,预测函数误分类的比率。
\[\varepsilon(h)=P^{(x,y)~\mathcal{D}}(h(x)\neq y)\]\(\varepsilon(h)\)表示泛化误差,\((x,y)\)表示被预测的样本,\(\mathcal{D}\)表示样本所遵循的概率分布。
注意:\(\hat\varepsilon(h)\)和\(\varepsilon(h)\)针对的样本集是不同的,后面定义的变量h和\(\hat h\)也遵循相同的约定。
这里我们假设:训练数据和预测数据都具有相同的概率分布\(\mathcal{D}\)。这个假设是PAC理论的假设之一。
PAC(Probably approximately correct)理论是Leslie Valiant于1984年提出的。这里的大部分讨论都和PAC有关。
Leslie Valiant,1949年生,英国计算机科学家,华威大学博士。哈佛大学教授,英国皇家学会会员,图灵奖获得者(2010)。
对于线性分类\(h_\theta(x)=1\{\theta^Tx\ge 0\}\)来说,寻找合适的参数\(\theta\),还有另一种方法,即最小化训练误差,并令:
\[\hat\theta=\arg\min_\theta\hat\varepsilon(h_\theta)\]我们将这个过程称为经验风险最小化(empirical risk minimization,ERM)。其最终的预测函数为\(\hat h=h_{\hat\theta}\)。
ERM是一类基本的学习算法,也是本节关注的焦点。
我们定义预测函数类(hypothesis class )\(\mathcal{H}\),用以表示解决某类学习问题的所有可能的分类器的集合。(实际上也就是参数\(\theta\)所有可能取值的集合。)则ERM算法可表示为:
\[\hat h=\arg\min_{h\in \mathcal{H}}\hat\varepsilon(h)\]参考:
http://www.jianshu.com/p/f1433317bf48
你真的理解机器学习中偏差-方差之间的权衡吗?
https://mp.weixin.qq.com/s/nRaM87Wao4XdHwltV1nh-A
思考VC维与PAC:如何理解深度神经网络中的泛化理论?
https://mp.weixin.qq.com/s/ty-V1JOzx24lLB8C0zHpaw
机器学习碎碎念:霍夫丁不等式
\(\mathcal{H}\)为有限集的情况
根据之前的讨论,我们做如下定义:
\[Z=1\{h_i(x)\neq y\}\] \[Z_j=1\{h_i(x^{(j)})\neq y^{(j)}\}\] \[\hat\varepsilon(h_i)=\frac{1}{m}\sum_{j=1}^mZ_j\]其中,\(h_i\in \mathcal{H}\)。
由Hoeffding不等式可知:
\[P(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)\le 2\exp(-2\gamma^2m)\]这个公式表明:对于特定的\(h_i\),在m很大的情况下,训练误差有很大的概率接近于泛化误差。
如果我们用\(A_i\)表示事件\(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma\),则上式可改为\(P(A_i)\le 2\exp(-2\gamma^2m)\)。
\[P(\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)=P(A_1\cup \dots\cup A_k)\] \[\le \sum_{i=1}^kP(A_i)\le \sum_{i=1}^k2\exp(-2\gamma^2m)=2k\exp(-2\gamma^2m)\] \[\begin{align} &1-P(\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma)=P(\lnot\exists h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert>\gamma) \\&=P(\forall h\in\mathcal{H}.\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le\gamma)\ge 1-2k\exp(-2\gamma^2m) \end{align}\]上面的结果表明,对于所有的\(h\in \mathcal{H}\),实际上也有一个收敛性质。这个性质被称为一致收敛(uniform convergence)。
上式变形可得:
\[m\ge \frac{1}{2\gamma^2}\log\frac{2k}{\delta}\]其中,\(\delta=2k\exp(-2\gamma^2m)\)。
上式表明,在固定\(\gamma\)和\(\delta\)的情况下,至少需要多少训练样本,才能保证对于所有的\(h\in \mathcal{H}\),\(P(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le \gamma)\)至少为\(1-\delta\)。
这里的m也被称为算法的样本复杂度(sample complexity),它表征达到一定性能所需要的训练样本的数量。
同样的,我们固定m和\(\delta\),可得:
\[\lvert\varepsilon(h)-\hat\varepsilon(h)\rvert\le \sqrt{\frac{1}{2m}\log\frac{2k}{\delta}}\]如果我们定义\(h^*=\arg\min_{h\in \mathcal{H}}\varepsilon(h)\),则根据一致收敛性质\(\lvert\varepsilon(h_i)-\hat\varepsilon(h_i)\rvert\le \gamma\)可得:
\[\varepsilon(\hat h)\le \hat\varepsilon(\hat h)+\gamma\]因为\(\hat h\)已经是\(\hat \varepsilon(h)\)中最小的一个,因此\(\hat\varepsilon(\hat h)\le \hat\varepsilon(h)\)对所有都是成立的,其中当然包括\(h^*\),即\(\hat\varepsilon(\hat h)\le \hat\varepsilon(h^*)\)。因此,上式可改为:
\[\varepsilon(\hat h)\le \hat\varepsilon(h^*)+\gamma\]根据一致收敛性质,我们还可以得出\(\hat\varepsilon(h^*)\le \varepsilon(h^*)+\gamma\),因此,上式继续变形为:
\[\varepsilon(\hat h)\le \varepsilon(h^*)+2\gamma\]这个公式表明,作为ERM结果的\(\hat h\),比最好的h,至多只差\(2\gamma\)。
我们将之前的结果合到一起,可得如下定理:
令\(\lvert\mathcal{H}\rvert=k\),并固定\(m,\delta\)的取值,且一致收敛的概率至少为\(1-\delta\),则:
\[\varepsilon(\hat h)\le \left(\min_{h\in \mathcal{H}}\varepsilon(h)\right)+2\sqrt{\frac{1}{2m}\log\frac{2k}{\delta}}\]假设我们需要从预测函数类\(\mathcal{H}\)切换到一个更大的预测函数类\(\mathcal{H'}\supseteq\mathcal{H}\),则上面公式的第一项只会变得更小,也就是说偏差会变小,但由于k的增加,第二项会变大,也就是方差会变大。
同理,可得以下针对m的定理:
令\(\lvert\mathcal{H}\rvert=k\),并固定\(\delta,\gamma\)的取值,为了保证\(\varepsilon(\hat h)\le \left(\min_{h\in \mathcal{H}}\varepsilon(h)\right)+2\gamma\)的概率至少为\(1-\delta\),则:
\[m\ge \frac{1}{2\gamma^2}\log\frac{2k}{\delta}=O\left(\frac{1}{\gamma^2}\log\frac{k}{\delta}\right)\]\(\mathcal{H}\)为无限集的情况
某些预测函数的参数是实数,它实际上包含了无穷多个数。针对这样的情况,我们可以参照IEEE浮点数的规则,进行离散采样。
IEEE浮点数由64bit的二进制数构成,因此d个实数参数组成的\(\mathcal{H}\),可组成\(k=2^{64d}\)个不同的预测函数,因此:
\[m\ge O\left(\frac{1}{\gamma^2}\log\frac{2^{64d}}{\delta}\right)=O\left(\frac{d}{\gamma^2}\log\frac{1}{\delta}\right)=O_{\gamma,\delta}(d)\]这里的下标\(\gamma,\delta\)表示一些依赖于它们的常量。从上式可以看出需要的训练样本的数量和预测模型的参数个数成线性关系。
以上就是和ERM相关的算法的理论知识,至于其他非ERM算法理论仍在研究之中。
下面是\(\mathcal{H}\)参数化的问题。一个线性分类器可以写为:
\[h_\theta(x)=1\{\theta_0+\theta_1x_1+\dots+\theta_nx_n\ge 0\}\]这种形式有\(n+1\)个参数。
但它也可以写为:
\[h_{u,v}(x)=1\{(u_0^2-v_0^2)+(u_0^2-v_0^2)x_1+\dots+(u_n^2-v_n^2)x_n\ge 0\}\]这种形式有\(2n+2\)个参数。
显然这两种形式在数学上是等价的,但参数的个数却不同。为此我们引入Vapnik-Chervonenkis维度(简称VC维度),用以刻画参数的个数。
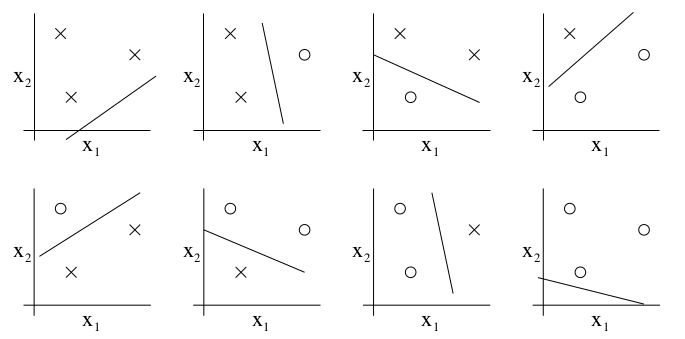
如上图所示,3个样本点有以上几种分布方式。毫无疑问,它们都能被\(h_\theta(x)=1\{\theta_0+\theta_1x_1+\theta_2x_2\ge 0\}\)所分割,且它们的训练误差为0。但如果是4个点的话,就不能无训练误差的分割了。我们将这种最大分割的个数称作VC维度,这里\(VC(\mathcal{H})=3\)。
需要注意的是,VC维度表征的是模型的最大切割能力,而不是针对所有的情况都成立。比如下图所示的三个点,就不可以被\(h_\theta(x)=1\{\theta_0+\theta_1x_1+\theta_2x_2\ge 0\}\)所分割,但这并不影响\(h_\theta(x)\)的VC维度值。
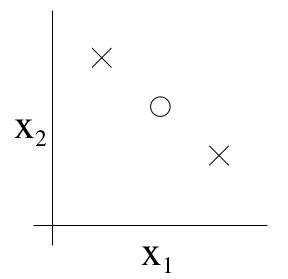
如果模型能切割任意大小的样本集,则\(VC(\mathcal{H})=\infty\)。
我们将VC维度值替换\(\mathcal{H}\)为有限集时的\(\lvert\mathcal{H}\rvert\),可得以下相关结论:
令\(VC(\mathcal{H})=d\),则:
\[\lvert\varepsilon(h)-\hat\varepsilon(h)\rvert\le O\left(\sqrt{\frac{d}{m}\log\frac{m}{d}+\frac{1}{m}\log\frac{1}{\delta}}\right)\] \[\varepsilon(\hat h)\le \varepsilon(h^*)+O\left(\sqrt{\frac{d}{m}\log\frac{m}{d}+\frac{1}{m}\log\frac{1}{\delta}}\right)\] \[m=O_{\gamma,\delta}(d)\]以上公式的其他条件,与\(\mathcal{H}\)为有限集时相同,这里不再赘述。

您的打赏,是对我的鼓励
