ML » 机器学习(一)——线性回归
2016-07-27 :: 6335 Words序
Machine Learning = Statistics + Optimization
Data Science = Machine Learning + Systems
—by Michael I. Jordan
这是根据Andrew Ng的《机器学习讲义》编写的系列blog。
吴恩达,英文名Andrew Ng,1976年生,华裔,在香港和新加坡长大。CMU本科+MIT硕士(1998年)+UCB博士(2002年)。斯坦福大学副教授,百度前首席科学家。
个人主页:
http://www.andrewng.org/
http://www.cnblogs.com/jerrylead/archive/2012/05/08/2489725.html
这是网友jerrylead翻译整理的版本,也是本文的一个重要的参考。
http://www.tcse.cn/~xulijie/
这是jerrylead的个人主页。
我写的版本在jerrylead版本的基础上,略有增删,添加了一下其他资料里的内容。
还有就是使用Mathjax+TeX书写公式,便于其他人的修改与传播。
该系列讲义实际上也就是网上非常知名的斯坦福CS229课程。该课程官网:
http://cs229.stanford.edu/syllabus.html
用吴恩达自己的话来说,他还拿着斯坦福教职,很大程度就是想教这门课。因此,该课程内容每年都有小幅更新。
它在coursera上也有个网页,内容相对简单一些(基本不讲数学公式,适合非算法岗的工程人员):
https://www.coursera.org/learn/machine-learning
除此之外,国立台湾大学林轩田教授的《机器学习基石》也是写的非常好的:
https://www.csie.ntu.edu.tw/~htlin/mooc/
参考:
https://mp.weixin.qq.com/s/5lpwvBr3oYnu36onF2S5EA
机器学习发展历史回顾
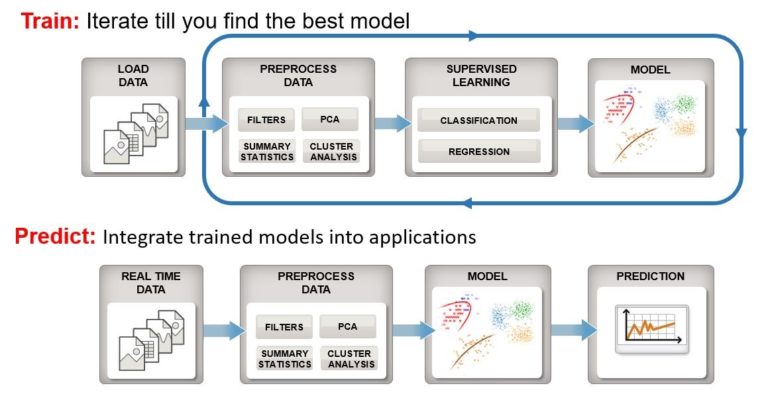
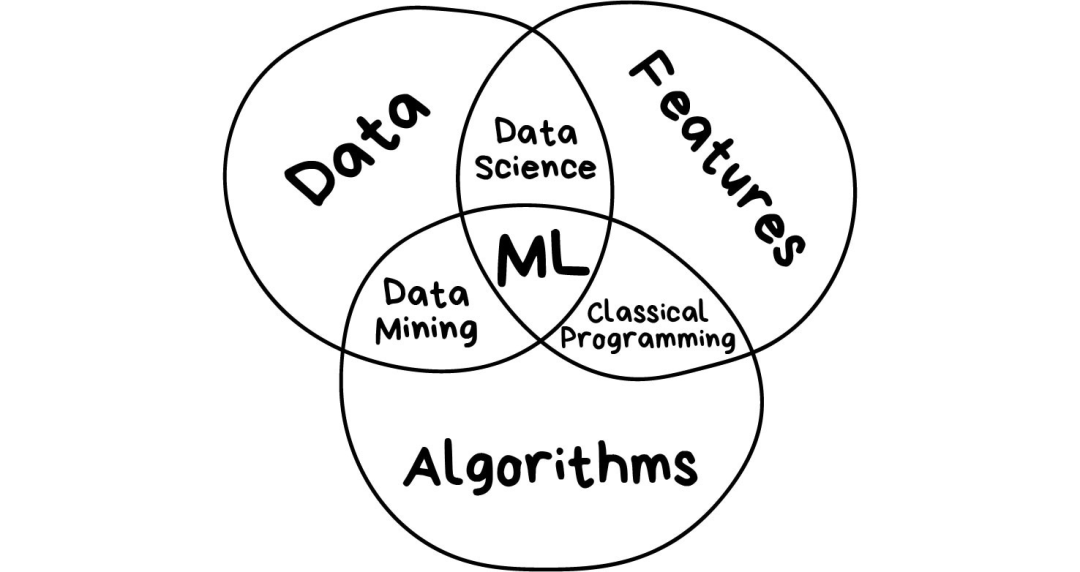
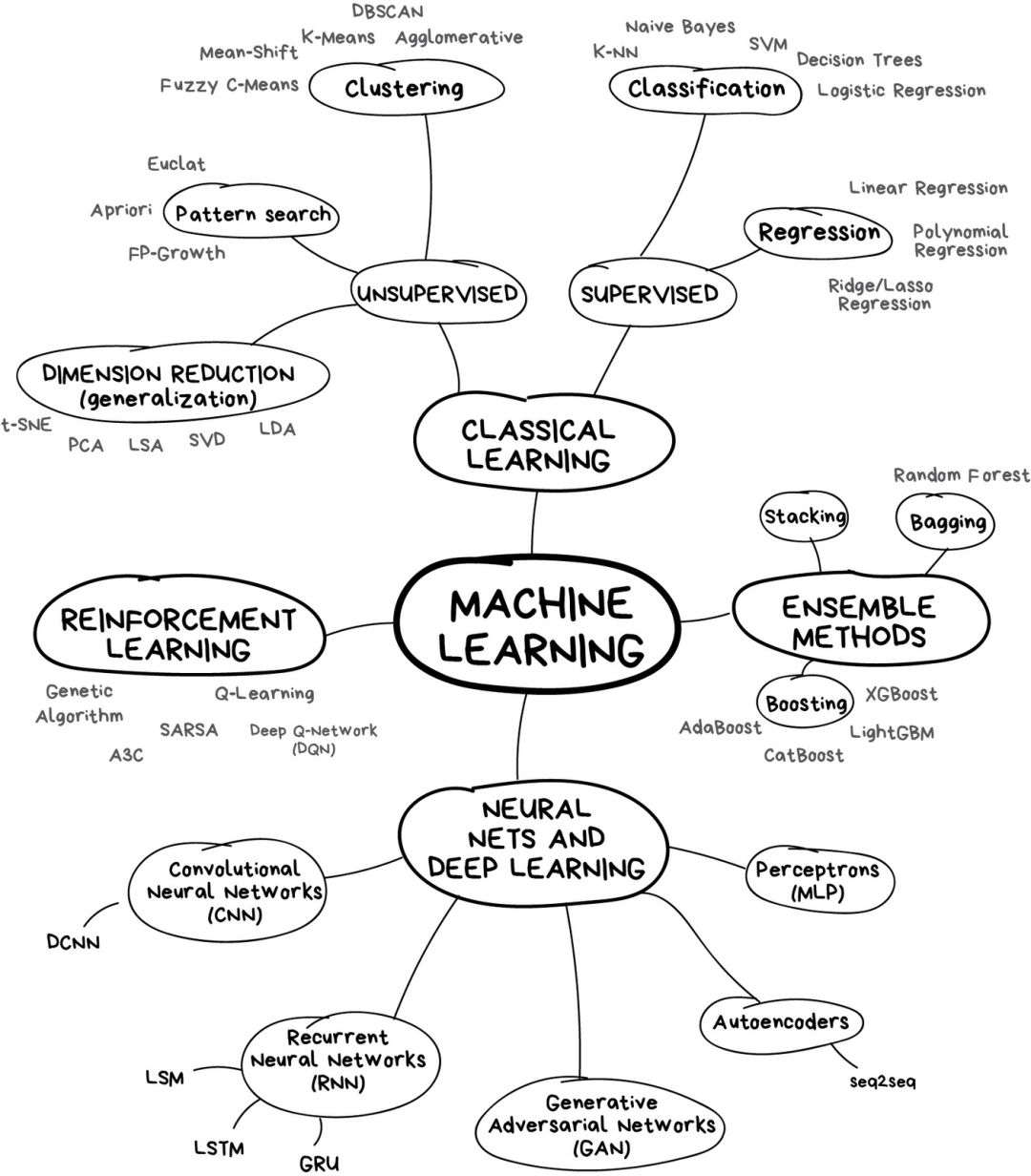
https://mp.weixin.qq.com/s/WiAlhSRT-02SryeMM5ecpA
机器学习的通俗讲解
线性回归
线性回归属于有监督学习(supervised learning)的其中一种方法。
对于一个给定的训练集(training set)\((x,y)\),其中\(y=h(x)=h(x_1,x_2,\dots,x_n)\),在\(h\)未知的情况下,求得\(h\)或者\(h\)的近似解的过程,被称为猜测(hypothesis)。hypothesis的目的是,能在给定\(x\)的情况下,预测\(y\)。
如果\(y\)是连续函数,那么这个过程叫做回归(regression)问题。如果\(y\)是离散函数,那么这个过程叫做分类(classification)问题。
\[h_{\theta}(x)=\theta_0+\theta_1x_1+\dots+\theta_nx_n=\sum_{i=0}^n\theta_ix_i=\theta^Tx \tag{1}\]满足公式1条件的回归问题,被称作线性回归(Linear Regression)。
为了评估公式1中待定系数\(\theta\)的预测准确度,我们定义如下代价函数(cost function):
\[J(\theta)=\frac{1}{2}\sum_{i=0}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 \tag{2}\]其中,m表示训练集的个数(从0算起),\(x^{(i)}\)表示第i个训练样本。
cost function,有的文章也称作loss function。
代价函数的表达式,实际上就是正态分布的方差计算公式,它体现了拟合后的函数曲线与样本集之间的偏差程度。显然,代价函数的值越小,预测准确度越高。
参考:
https://mp.weixin.qq.com/s/wGoT6XCLuvTcQB62-hb78Q
线性回归:简单线性回归详解
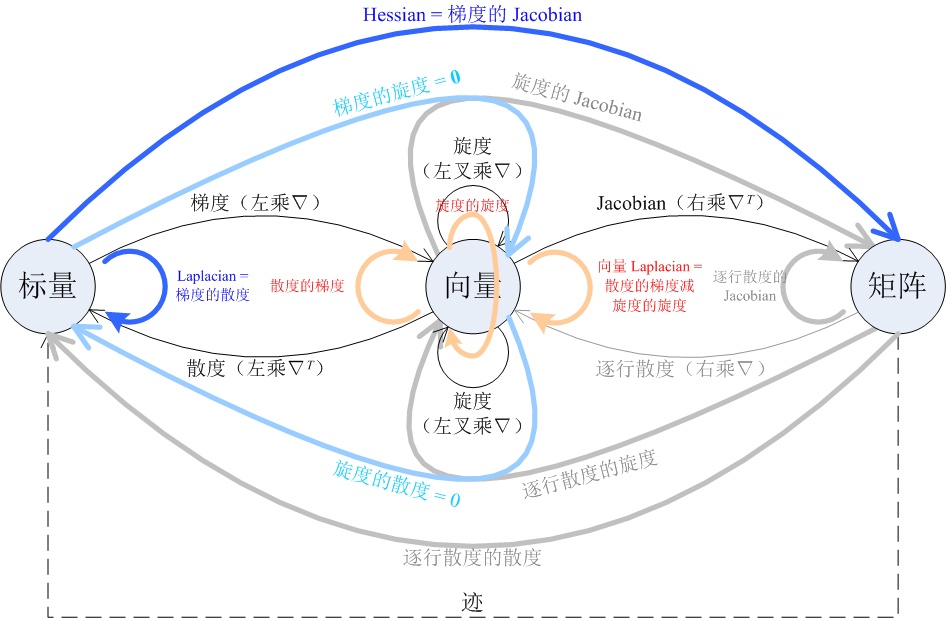
Jacobian矩阵
Jacobian矩阵是矩阵A的一阶导数矩阵,定义如下:
\[J(A)=\frac{\mathrm{d}f}{\mathrm{d}x}= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}\]Carl Gustav Jacob Jacobi,1804~1851,德国数学家,柏林大学博士。
当\(m=1\)时,该矩阵又被称为梯度向量:
\[\nabla(A)=\begin{bmatrix} \frac{\partial f}{\partial x_1} & \cdots & \frac{\partial f}{\partial x_n} \\ \end{bmatrix}\]Hessian矩阵
Hessian矩阵是矩阵A的二阶导数矩阵,定义如下:
\[H(A)= \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\partial x_n} \\ \frac{\partial^2 f}{\partial x_2\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n\partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\ \end{bmatrix}\]Ludwig Otto Hesse,1811~1874,德国数学家,毕业于柯尼斯堡大学,Jacobi的学生。
因为\(\frac{\partial^2 f}{\partial x_i\partial x_j}=\frac{\partial^2 f}{\partial x_j\partial x_i}\)(克莱罗定理,Clairaut’s theorem),所以Hessian矩阵通常是一个对称矩阵。
参考:
http://blog.csdn.net/dsbatigol/article/details/12558891
梯度(gradient)、雅克比矩阵(Jacobian)、海森矩阵(Hessian)
http://files.cnblogs.com/files/leoleo/matrix_rules.pdf
矩阵、向量求导法则全览
https://zhuanlan.zhihu.com/p/35323714
梯度、散度、旋度、Jacobian、Hessian、Laplacian的关系图
https://mp.weixin.qq.com/s/869EVyCmYPQKBA-kdo0lNQ
张量101
https://mp.weixin.qq.com/s/iEi2UWEwxsO5C8Ra74jFaQ
张量求导和计算图
梯度下降算法
公式2的求极值问题,实际上就是求驻点(stationary point)的问题,即求\(\nabla(f)=0\)的点的问题。
梯度下降(gradient descent)算法的原理,从直观来说,就是沿着梯度向量的反方向,向坡底前进。该算法是一个递归算法,其迭代公式为:
\[x_{k+1}=x_k-t_kA_k\nabla f(x_k)\]其中,\(t_k\)表示迭代的步长,\(\nabla f(x_k)\)为梯度向量,\(A_k\)为系数矩阵。根据\(t_k\)和\(A_k\)的取法不同会产生出各种各样的变种算法。
例如,当\(A_k=H(x_k)^{-1}\)时,就是著名的牛顿迭代法(Newton Method)。可以证明,牛顿迭代法具有二阶收敛性(在二阶以内的所有系数矩阵中,收敛最快)。
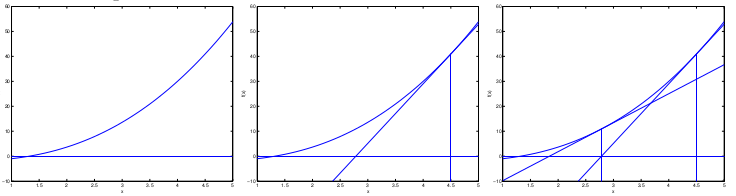
| 名称 | 梯度下降算法 | 牛顿迭代法 |
|---|---|---|
| 迭代次数 | 收敛慢,迭代次数多。 | 收敛快,迭代次数少。 |
| 迭代计算复杂度 | \(O(n)\) | \(O(n^3)\) |
| 实现难点 | 步长需要一定的方法来确定。 | \(H(x_k)\)需要满秩,且\(H(x_k)^{-1}\)的计算比较复杂,尤其是维数很高的时候。 |
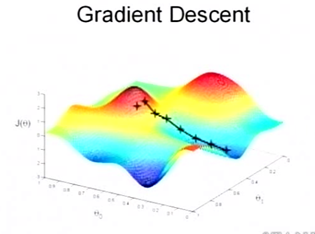
梯度下降算法只有当函数为凸函数时,才会严格收敛到最小值。否则的话,可能只是极小值,而非最小值。如下图所示:
凸集(Convex set)的图例如下所示:
 |
 |
 |
| Convex set | non-Convex set | convex function |
某牛语录:
虽然Newton Method收敛快,只需要很少次的迭代,但是每一步迭代的计算量却比普通的Gradient Descent要大很多:Gradient Descent只要计算一个d维Gradient向量即可,Newton Method不仅要计算Hessian矩阵(\(d^2\)维),而且要对该矩阵求逆(或者是解线性方程组)——对于通常的dense矩阵,这是一个复杂度为\(O(d^3)\)的操作。
更严重的是,如果数据的维度非常高,且不说后面的求逆操作,即使Hessian矩阵本身的求解甚至存储都会出现问题。有时候碰到的情况是连Newton Method迭代一次的计算量都承担不起,所以在大规模机器学习或者general的大规模优化问题中,简单的一阶(只需要用到gradient信息)算法得到了更多的关注。
例如Interior Point Method的发明被认为是Optimization中的重要里程碑,这一类的方法能够保证在多项式次迭代内收敛。但是在机器学习中,特别是现在的所谓“大数据”的趋势下,这类算法却没法工作,一方面由于机器学习中所处理的数据通常维度非常高,从而相应的优化问题的变量个数变得很巨大,传统的方法虽然保证多项式迭代收敛,但是其中每一步迭代的计算代价却是随着变量个数的平方甚至三次方增长,结果是连算法的一次迭代都无法在可接受的时间内完成。
参考:
http://freemind.pluskid.org/machine-learning/gradient-descent-wolfe-s-condition-and-logistic-regression/
Gradient Descent, Wolfe’s Condition and Logistic Regression
http://freemind.pluskid.org/machine-learning/newton-method/
Newton Method
https://mp.weixin.qq.com/s/7fk6-gK-gpnWubEr_i7aAg
通俗理解凸函数及它的一阶特征
https://mp.weixin.qq.com/s/lzZANmhfJeEtIayIoqjMOw
通俗讲解凸函数及它的二阶特征
https://mp.weixin.qq.com/s/oJU8ccIamK9UcU1tgmyFeg
凸集、凸函数与凸优化基本概念
https://mp.weixin.qq.com/s/iBPhhNJYF3gayBU2NHI8jw
谈非线性规划的一维搜索各种方法!
http://mp.weixin.qq.com/s/yjay4tEYPMUW-V10BxG_7Q
为什么梯度的负方向是局部下降最快的方向?
LMS算法
LMS(least mean squares,最小均方)算法,也是一种迭代算法。其迭代公式为:
\[\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta_j} \tag{3}\]其中,\(:=\)表示赋值操作,\(J(\theta)\)是公式2所示的代价函数,\(\alpha\)被称作学习率(learning rate)。
可以看出,LMS的迭代公式是梯度下降算法的一个特例,其中,\(\alpha\)相当于步长,系数矩阵\(A=E\),这里的\(E\)表示单位矩阵。
将公式2代入公式3,可得:
\[\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j \tag{4}\]迭代方式很多,常见的有以下几种:
1.批量梯度下降(Batch Gradient Descent)。方法如下:
Repeat until convergence {
\(\theta_j:=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j\)(for every j)
}
2.随机梯度下降(Stochastic Gradient Descent)。方法如下:
Loop {
for i=1 to m, {
\(\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j\)(for every j)
}
}
| 名称 | 批量梯度下降 | 随机梯度下降 |
|---|---|---|
| 特点 | 每向前走一步,都需要遍历整个训练样本集。 | 一个样本接着一个样本的处理数据。 |
| 计算复杂度 | 大 | 小 |
| 收敛程度 | 收敛 | 由于新样本引入新的误差,该算法只能收敛到一定程度,而不能无限逼近最小值。 |
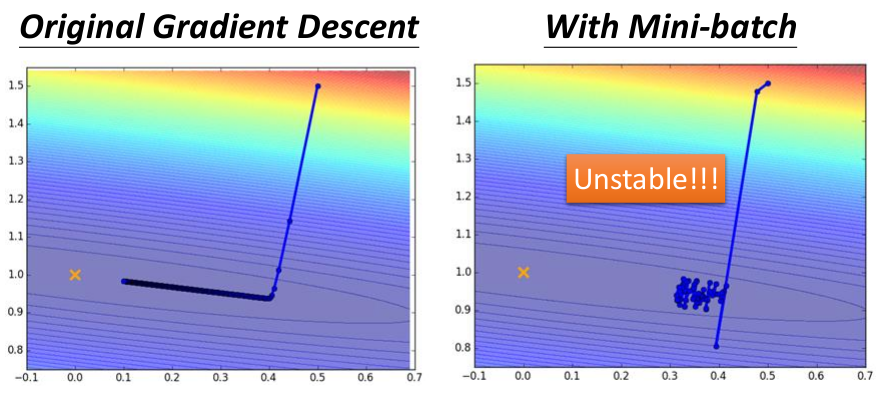
3.Mini-batch Gradient Descent,这种方法的行为和效果介于前两者之间。

您的打赏,是对我的鼓励
